人教版 数学三年级下册 第2单元 商中间有0的除法 教案
文档属性
| 名称 | 人教版 数学三年级下册 第2单元 商中间有0的除法 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 222.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 13:10:48 | ||
图片预览




文档简介
第课时 商中间有0的除法
1.知道“0除以任何不是0的数都得0”。
2.使学生掌握商中间有0的除法的计算方法,能正确计算商中间有0的除法。
3.培养学生笔算除法的能力,养成验算的习惯。
4.使学生感受数学与生活的联系,能够运用所学知识解决日常生活中的简单问题。
【重点】
掌握“0除以任何不是0的数都得0”,正确、熟练计算“商中间有0的除法”。
【难点】
商中间有0的除法的两种情况。
【教师准备】 PPT课件。
1.口算(说说你是怎样算的)。
60÷3 240÷8
42×0 9×0
(学生每算一题,说一说自己的口算方法)
2.不计算,判断商是几位数。
292÷2 358÷6 488÷4
【参考答案】 1.20 30 0 0 2.三位数 两位数 三位数
笔算是以口算为基础的,只有加强口算训练才能提高笔算的速度和正确率,同时安排此口算的目的是让学生回顾数中有0的口算方法,为本课打下基础。不计算判断商是几位数的训练,让学生进一步检验商的位数,为下面学习商中间或末尾有0的笔算除法奠定基础。
故事导入。
师讲猪八戒分西瓜的故事:话说这一天唐僧师徒四人来到一个山坡前,他们又累又渴,便坐下来休息,唐僧师傅吩咐悟空去化些斋饭来。一会工夫,悟空找来四个大西瓜。
这时出示问题:4个西瓜,师徒4人,平均每人吃几个
预设 生:列式4÷4=1。
师:怎样算出的得数
预设 生:根据乘法口诀求商。
师继续讲故事:这时猪八戒非常积极地说:“我来分。”贪吃的猪八戒看到西瓜嘴馋了,他想反正有4个,我吃掉一个吧,就这样他一个又一个地把4个西瓜全吃完了,这下他怎么分给孙悟空、沙和尚和唐僧啊 (老师借机对学生进行思想教育)
师:西瓜一个都没有了,用哪个数表示
0个西瓜平均分给3人,每人可以分到多少 谁会算
这就是我们今天要学习的内容。
俗话说,好的开始是成功的一半,借助讲学生喜欢的故事,一下子抓住学生的学习兴趣,调动了学生学习的积极性,也让学生时时体会到数学与生活的联系。
师板书:39。
请学生说出3和9各表示的意义。
师板书:0。
请学生说出0表示的意义。
师:在3和9的中间添上一个0,使39变成“309”,请同学说出0在这个位置表示的意义是什么。
(揭示课题)这节课我们将学习有关0的除法。(板书课题:商中间有0的除法)
本单元所教学的计算基本上都是从解决生活实际问题出发,使学生领悟到除法在生活中的作用。采用在数字中加0的方法激发学生的学习兴趣。
谈话导入。
师用通俗的语言讲述数学历史上一个关于0的小故事,让学生谈一下对0的理解。
让学生在数学历史的故事中了解0的由来和发展,明白0是“没有”“空白”的意思。
一、探究0除以任何不是0的数,都得0
(PPT课件出示教材第23页例5)
师:0除以5究竟等于多少 你是怎么想的
预设 生1:等于0,因为把0个东西平均分给5个人,什么都分不到。
生2:0除以5等于0,因为我们在二年级学过算除法想乘法,只有0乘5等于0,所以0除以5得0。
师:你们真会动脑筋。那你们能算出0除以4,0除以9,0除以376分别等于多少吗 为什么 从这些算式中你发现了什么规律
预设 生1:0除以任何数都得0。
生2:任何数除0都得0。
师:如果0除以0行不行 等于多少呢
预设 生:0除以0得0。
师:我认为得1也对呀 (在0÷0的算式后面写上“=1”)
预设 生:不对。
师:怎么不对 因为0乘1也等于0啊,所以0除以0就等于1。
师依次写出等于2,3,4……让他们判断,此时学生恍然大悟:当0除以0时找不到一个准确的商。
师:2除以0等于多少 能说说你的理由吗 引导学生从平均分的意义和乘除法的关系得出:当0作除数时没有实际意义,从而理解“0除以任何不是0的数都得0”的道理。
概括:0除以任何不是0的数都得0。
师:刚才同学们通过“观察——思考——验证”,知道了0除以任何不是0的数都得0。接下来我们就运用这个结论来学习“商中间有0的除法”。
二、探究商中间有0的除法的计算方法
(PPT课件出示教材第23页例6)
师:从图中你知道了哪些信息 可以提出哪些问题
预设 生1:买2套中国古典名著,平均每套多少元
生2:买2套世界名著,平均每套多少元
师:怎样列式计算
根据学生回答分别板书:208÷2 216÷2
1.探究商中间有0的第一种情况。
(1)(师出示)208÷2=
提出问题:
师:①不计算,你知道商是几位数吗
②估算商大约是多少
③准确结果是多少呢 请同学们自己试着算一算。你在计算过程中遇到了什么问题 是怎样解决的
先独立探索,再和小组的同学交流一下算法。
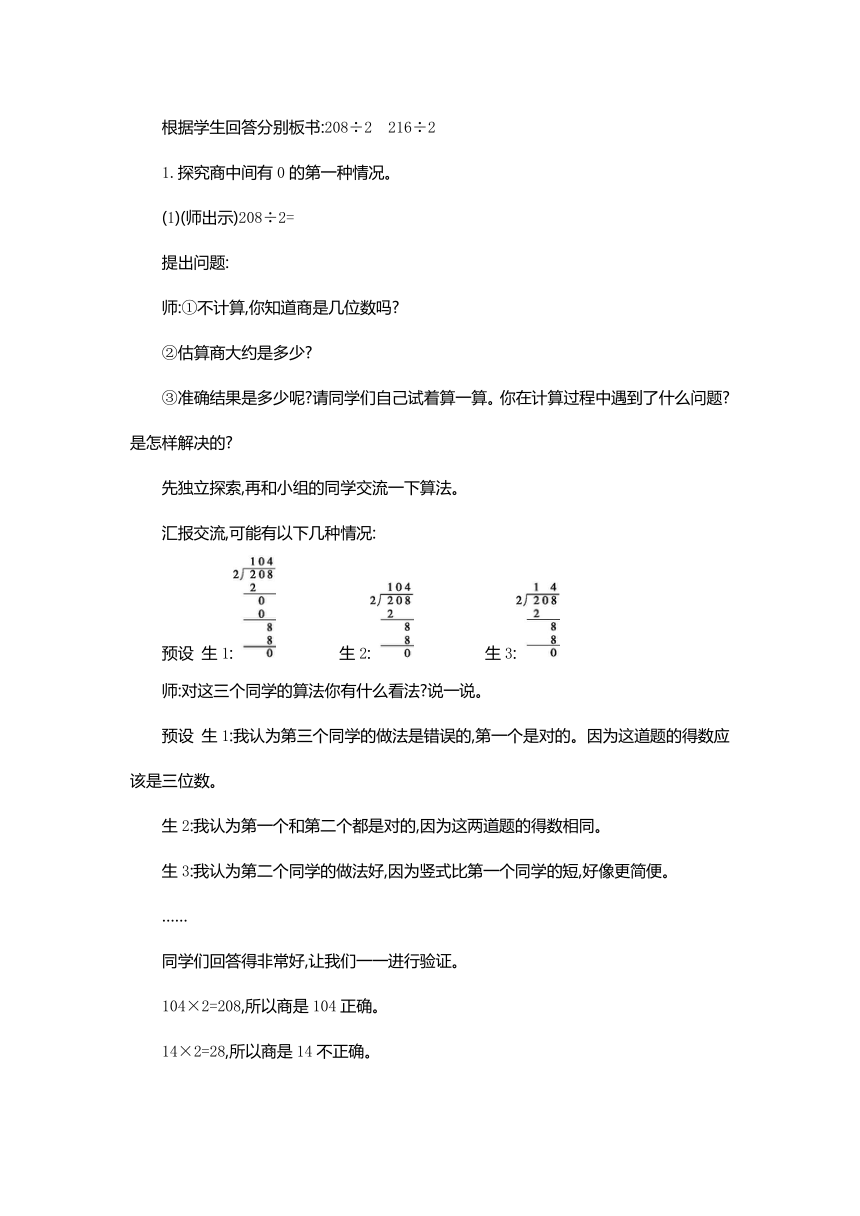
汇报交流,可能有以下几种情况:
预设 生1: 生2: 生3:
师:对这三个同学的算法你有什么看法 说一说。
预设 生1:我认为第三个同学的做法是错误的,第一个是对的。因为这道题的得数应该是三位数。
生2:我认为第一个和第二个都是对的,因为这两道题的得数相同。
生3:我认为第二个同学的做法好,因为竖式比第一个同学的短,好像更简便。
……
同学们回答得非常好,让我们一一进行验证。
104×2=208,所以商是104正确。
14×2=28,所以商是14不正确。
(2)板演过程,结合板演点拨:被除数百位上的2正好除尽,被除数十位上的0除以2商是几呢 商0,0乘2得0,十位上除尽,商十位上也就是中间的0能够省略吗 (不能够,0起到占位的作用)
(3)独立完成简便方法,板书简便写法,小组内互相说一说计算过程。(指名说,完成做一做)
2.探究商中间有0的第二种情况。
师:买2套世界名著,求平均每套多少元,又该如何计算
预设 生1:216÷2,可是老师十位上不够除
生2:老师,这个好解决,我们之前算有余数除法时,遇到不够除的情况,用0占位。
师:你真是个聪明的孩子,会把前面学过的知识运用到解决问题中,真棒!(这时学生的积极性异常高涨)
预设 生:老师,那么剩下的十位和个位上的数可以按照首位不够除的办法解决。
师:你真棒!看来只要用心观察、认真思考,问题就会迎刃而解。那么我们就用他说的办法计算。
师生交流板书:216÷2,百位上商1,正好除尽;把十位上的“1”落下来,不够除,我们在十位上商“0”占位,把个位上的“6”落下来,16除以2,在个位上商8,正好除尽。
预设 生1:老师,我还发现:三位数除以一位数时,不光是被除数中间有0,商的中间可能会有0,被除数的中间没有0,十位不够除,商也会出现中间有0的情况。
生2:老师他说得不完全对,必须是三位数除以一位数,且被除数的首位能除尽,被除数十位上的数是0或比除数小时,商中间就会有0。
师:大家快为他鼓鼓掌吧!你真是太棒了!都能成为一个小数学家了!看来,我们大家只要勤动脑思考,未来的数学家一定就会在你们中间产生。
让学生先自主计算,尝试解决计算中遇到的问题,再通过竖式简便和不简便的计算进行对照,让学生在通过直观的对比理解,当商的十位或个位上为0时,这个0一定要写,0起占位的作用;由于0除以任何不是0的数都得0,因此,写竖式的时候,可以省略用0作被除数的笔算过程,得出竖式的简便写法。
在学习了208÷2的笔算竖式的简便方法后,再让学生自主探索216÷2的计算方法,把学习的主动权真正交给学生,使学生亲历知识形成过程,收获到自主探索的乐趣。
练习1
展示409÷3=103板书错例,为什么不在商中间直接写0 (前一位有余数)对比309÷3和409÷3的笔算过程,观察百位计算后的结果有什么不同
【参考答案】 结论:当被除数的百位正好除尽,十位的数是0时,就直接商0,省略笔算过程。
旨在通过对比,错例分析,使学生明白只有当被除数的百位正好除尽,十位的数是0时,才可以直接商0,省略笔算过程。通过改错,让学生巩固“占位”方法,避免出错。
练习2
完成相关习题。
今天这节课我们通过学习知道了0除以任何不是0的数都得0,通过观察、思考、发现,自主探究,弄清了商中间的0必须写,它起到占位的作用,希望同学们在今后做题中一定要注意。
作业1
教材第24页做一做,教材第26页练习五第1,3,4题。
作业2
完成相关习题。
商中间有0的除法 208÷2=104(元) 216÷2=108(元) 简便写法: 简便写法:
新课标重视学生学习过程的体验。在教学“商中间有0的除法”时,学生在试一试、算一算等过程中,给自己提供一种自我探索、自我思考、自我创造、自我表现和自我实现的实践机会,从而真正理解了“0除以任何不是0的数都得0”的规律,掌握了商中间有0的除法计算方法。
教师驾驭课堂的能力有待进一步加强,方能很好地掌握课堂节奏,充分利用有限的时间,引导学生自主、合作学习。
学生试商是一个难点,突破这一难点需要进行有针对性的练习。再教学时可让学生先估一估商是几位数,再计算,这样可以降低错误率。在解决问题时,培养学生对计算结果或问题答案进行估计,尽量让学生亲自动手尝试208÷2的算法,在此基础上让学生试着用竖式计算,学生在写竖式时,有的采用原有写法,但也有的用简便写法。通过两种不同写法学生的介绍及集体探讨研究,让学生感受到这样列竖式计算很简便,产生要学好这种简便写法的需要,并在不知不觉中理解算理,充分体现学生的自主性。
放假了,宁宁一家准备去青岛旅游,他们走访了两家旅行社,其价格如下:
山水旅行社:青岛三日游,4人408元。
青年旅行社:青岛三日游,5人505元。
请你为宁宁一家选择一家价格便宜的旅行社。
[名师点拨] 要想知道哪家旅行社最便宜,就要算出每家旅行社每人去青岛旅行需要多少钱。
[解答] 408÷4=102(元) 505÷5=101(元)
102元>101元,青年旅行社的价格便宜。
【知识拓展】 三位数除以一位数,商的中间有0的笔算除法的计算方法可以推广到多位数除以一位数时,商的中间有0的笔算除法中去,只不过可能商的中间0的个数增加了。
如何判断商的位数
三年级学生在初学一位数除多位数,尤其是被除数中间或末尾有0的除法时,往往会出现漏商现象。那么怎样才能防止漏商呢 只有学会正确地判断商的位数。
判断商是几位数的方法:当被除数最高位上的数大于或等于除数时,商的位数等于被除数的位数;当被除数最高位上的数比除数小时,商的位数比被除数少一位。如:
(1)8700÷6,被除数的最高位上的数是8,8比除数6大,所以商的位数与被除数的位数相等,即商是四位数。
(2)312÷3,被除数最高位上的数是3,3与除数3相等,所以商的位数等于被除数的位数,即商是三位数。
(3)2480÷8,被除数最高位上的数是2,2比除数8小,所以商的位数比被除数少一位,即商是三位数。
你学会了吗 请你判断下面各题的商是几位数,然后再计算。
720÷6 2800÷8 7500÷5
481÷4 4007÷8
【参考答案】 三位数 120 三位数 350 四位数 1500 三位数 120……1 三位数 500……7
1.知道“0除以任何不是0的数都得0”。
2.使学生掌握商中间有0的除法的计算方法,能正确计算商中间有0的除法。
3.培养学生笔算除法的能力,养成验算的习惯。
4.使学生感受数学与生活的联系,能够运用所学知识解决日常生活中的简单问题。
【重点】
掌握“0除以任何不是0的数都得0”,正确、熟练计算“商中间有0的除法”。
【难点】
商中间有0的除法的两种情况。
【教师准备】 PPT课件。
1.口算(说说你是怎样算的)。
60÷3 240÷8
42×0 9×0
(学生每算一题,说一说自己的口算方法)
2.不计算,判断商是几位数。
292÷2 358÷6 488÷4
【参考答案】 1.20 30 0 0 2.三位数 两位数 三位数
笔算是以口算为基础的,只有加强口算训练才能提高笔算的速度和正确率,同时安排此口算的目的是让学生回顾数中有0的口算方法,为本课打下基础。不计算判断商是几位数的训练,让学生进一步检验商的位数,为下面学习商中间或末尾有0的笔算除法奠定基础。
故事导入。
师讲猪八戒分西瓜的故事:话说这一天唐僧师徒四人来到一个山坡前,他们又累又渴,便坐下来休息,唐僧师傅吩咐悟空去化些斋饭来。一会工夫,悟空找来四个大西瓜。
这时出示问题:4个西瓜,师徒4人,平均每人吃几个
预设 生:列式4÷4=1。
师:怎样算出的得数
预设 生:根据乘法口诀求商。
师继续讲故事:这时猪八戒非常积极地说:“我来分。”贪吃的猪八戒看到西瓜嘴馋了,他想反正有4个,我吃掉一个吧,就这样他一个又一个地把4个西瓜全吃完了,这下他怎么分给孙悟空、沙和尚和唐僧啊 (老师借机对学生进行思想教育)
师:西瓜一个都没有了,用哪个数表示
0个西瓜平均分给3人,每人可以分到多少 谁会算
这就是我们今天要学习的内容。
俗话说,好的开始是成功的一半,借助讲学生喜欢的故事,一下子抓住学生的学习兴趣,调动了学生学习的积极性,也让学生时时体会到数学与生活的联系。
师板书:39。
请学生说出3和9各表示的意义。
师板书:0。
请学生说出0表示的意义。
师:在3和9的中间添上一个0,使39变成“309”,请同学说出0在这个位置表示的意义是什么。
(揭示课题)这节课我们将学习有关0的除法。(板书课题:商中间有0的除法)
本单元所教学的计算基本上都是从解决生活实际问题出发,使学生领悟到除法在生活中的作用。采用在数字中加0的方法激发学生的学习兴趣。
谈话导入。
师用通俗的语言讲述数学历史上一个关于0的小故事,让学生谈一下对0的理解。
让学生在数学历史的故事中了解0的由来和发展,明白0是“没有”“空白”的意思。
一、探究0除以任何不是0的数,都得0
(PPT课件出示教材第23页例5)
师:0除以5究竟等于多少 你是怎么想的
预设 生1:等于0,因为把0个东西平均分给5个人,什么都分不到。
生2:0除以5等于0,因为我们在二年级学过算除法想乘法,只有0乘5等于0,所以0除以5得0。
师:你们真会动脑筋。那你们能算出0除以4,0除以9,0除以376分别等于多少吗 为什么 从这些算式中你发现了什么规律
预设 生1:0除以任何数都得0。
生2:任何数除0都得0。
师:如果0除以0行不行 等于多少呢
预设 生:0除以0得0。
师:我认为得1也对呀 (在0÷0的算式后面写上“=1”)
预设 生:不对。
师:怎么不对 因为0乘1也等于0啊,所以0除以0就等于1。
师依次写出等于2,3,4……让他们判断,此时学生恍然大悟:当0除以0时找不到一个准确的商。
师:2除以0等于多少 能说说你的理由吗 引导学生从平均分的意义和乘除法的关系得出:当0作除数时没有实际意义,从而理解“0除以任何不是0的数都得0”的道理。
概括:0除以任何不是0的数都得0。
师:刚才同学们通过“观察——思考——验证”,知道了0除以任何不是0的数都得0。接下来我们就运用这个结论来学习“商中间有0的除法”。
二、探究商中间有0的除法的计算方法
(PPT课件出示教材第23页例6)
师:从图中你知道了哪些信息 可以提出哪些问题
预设 生1:买2套中国古典名著,平均每套多少元
生2:买2套世界名著,平均每套多少元
师:怎样列式计算
根据学生回答分别板书:208÷2 216÷2
1.探究商中间有0的第一种情况。
(1)(师出示)208÷2=
提出问题:
师:①不计算,你知道商是几位数吗
②估算商大约是多少
③准确结果是多少呢 请同学们自己试着算一算。你在计算过程中遇到了什么问题 是怎样解决的
先独立探索,再和小组的同学交流一下算法。
汇报交流,可能有以下几种情况:
预设 生1: 生2: 生3:
师:对这三个同学的算法你有什么看法 说一说。
预设 生1:我认为第三个同学的做法是错误的,第一个是对的。因为这道题的得数应该是三位数。
生2:我认为第一个和第二个都是对的,因为这两道题的得数相同。
生3:我认为第二个同学的做法好,因为竖式比第一个同学的短,好像更简便。
……
同学们回答得非常好,让我们一一进行验证。
104×2=208,所以商是104正确。
14×2=28,所以商是14不正确。
(2)板演过程,结合板演点拨:被除数百位上的2正好除尽,被除数十位上的0除以2商是几呢 商0,0乘2得0,十位上除尽,商十位上也就是中间的0能够省略吗 (不能够,0起到占位的作用)
(3)独立完成简便方法,板书简便写法,小组内互相说一说计算过程。(指名说,完成做一做)
2.探究商中间有0的第二种情况。
师:买2套世界名著,求平均每套多少元,又该如何计算
预设 生1:216÷2,可是老师十位上不够除
生2:老师,这个好解决,我们之前算有余数除法时,遇到不够除的情况,用0占位。
师:你真是个聪明的孩子,会把前面学过的知识运用到解决问题中,真棒!(这时学生的积极性异常高涨)
预设 生:老师,那么剩下的十位和个位上的数可以按照首位不够除的办法解决。
师:你真棒!看来只要用心观察、认真思考,问题就会迎刃而解。那么我们就用他说的办法计算。
师生交流板书:216÷2,百位上商1,正好除尽;把十位上的“1”落下来,不够除,我们在十位上商“0”占位,把个位上的“6”落下来,16除以2,在个位上商8,正好除尽。
预设 生1:老师,我还发现:三位数除以一位数时,不光是被除数中间有0,商的中间可能会有0,被除数的中间没有0,十位不够除,商也会出现中间有0的情况。
生2:老师他说得不完全对,必须是三位数除以一位数,且被除数的首位能除尽,被除数十位上的数是0或比除数小时,商中间就会有0。
师:大家快为他鼓鼓掌吧!你真是太棒了!都能成为一个小数学家了!看来,我们大家只要勤动脑思考,未来的数学家一定就会在你们中间产生。
让学生先自主计算,尝试解决计算中遇到的问题,再通过竖式简便和不简便的计算进行对照,让学生在通过直观的对比理解,当商的十位或个位上为0时,这个0一定要写,0起占位的作用;由于0除以任何不是0的数都得0,因此,写竖式的时候,可以省略用0作被除数的笔算过程,得出竖式的简便写法。
在学习了208÷2的笔算竖式的简便方法后,再让学生自主探索216÷2的计算方法,把学习的主动权真正交给学生,使学生亲历知识形成过程,收获到自主探索的乐趣。
练习1
展示409÷3=103板书错例,为什么不在商中间直接写0 (前一位有余数)对比309÷3和409÷3的笔算过程,观察百位计算后的结果有什么不同
【参考答案】 结论:当被除数的百位正好除尽,十位的数是0时,就直接商0,省略笔算过程。
旨在通过对比,错例分析,使学生明白只有当被除数的百位正好除尽,十位的数是0时,才可以直接商0,省略笔算过程。通过改错,让学生巩固“占位”方法,避免出错。
练习2
完成相关习题。
今天这节课我们通过学习知道了0除以任何不是0的数都得0,通过观察、思考、发现,自主探究,弄清了商中间的0必须写,它起到占位的作用,希望同学们在今后做题中一定要注意。
作业1
教材第24页做一做,教材第26页练习五第1,3,4题。
作业2
完成相关习题。
商中间有0的除法 208÷2=104(元) 216÷2=108(元) 简便写法: 简便写法:
新课标重视学生学习过程的体验。在教学“商中间有0的除法”时,学生在试一试、算一算等过程中,给自己提供一种自我探索、自我思考、自我创造、自我表现和自我实现的实践机会,从而真正理解了“0除以任何不是0的数都得0”的规律,掌握了商中间有0的除法计算方法。
教师驾驭课堂的能力有待进一步加强,方能很好地掌握课堂节奏,充分利用有限的时间,引导学生自主、合作学习。
学生试商是一个难点,突破这一难点需要进行有针对性的练习。再教学时可让学生先估一估商是几位数,再计算,这样可以降低错误率。在解决问题时,培养学生对计算结果或问题答案进行估计,尽量让学生亲自动手尝试208÷2的算法,在此基础上让学生试着用竖式计算,学生在写竖式时,有的采用原有写法,但也有的用简便写法。通过两种不同写法学生的介绍及集体探讨研究,让学生感受到这样列竖式计算很简便,产生要学好这种简便写法的需要,并在不知不觉中理解算理,充分体现学生的自主性。
放假了,宁宁一家准备去青岛旅游,他们走访了两家旅行社,其价格如下:
山水旅行社:青岛三日游,4人408元。
青年旅行社:青岛三日游,5人505元。
请你为宁宁一家选择一家价格便宜的旅行社。
[名师点拨] 要想知道哪家旅行社最便宜,就要算出每家旅行社每人去青岛旅行需要多少钱。
[解答] 408÷4=102(元) 505÷5=101(元)
102元>101元,青年旅行社的价格便宜。
【知识拓展】 三位数除以一位数,商的中间有0的笔算除法的计算方法可以推广到多位数除以一位数时,商的中间有0的笔算除法中去,只不过可能商的中间0的个数增加了。
如何判断商的位数
三年级学生在初学一位数除多位数,尤其是被除数中间或末尾有0的除法时,往往会出现漏商现象。那么怎样才能防止漏商呢 只有学会正确地判断商的位数。
判断商是几位数的方法:当被除数最高位上的数大于或等于除数时,商的位数等于被除数的位数;当被除数最高位上的数比除数小时,商的位数比被除数少一位。如:
(1)8700÷6,被除数的最高位上的数是8,8比除数6大,所以商的位数与被除数的位数相等,即商是四位数。
(2)312÷3,被除数最高位上的数是3,3与除数3相等,所以商的位数等于被除数的位数,即商是三位数。
(3)2480÷8,被除数最高位上的数是2,2比除数8小,所以商的位数比被除数少一位,即商是三位数。
你学会了吗 请你判断下面各题的商是几位数,然后再计算。
720÷6 2800÷8 7500÷5
481÷4 4007÷8
【参考答案】 三位数 120 三位数 350 四位数 1500 三位数 120……1 三位数 500……7
