华东师大版七年级下册数学 第9章 多边形复习课件 (共18张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 第9章 多边形复习课件 (共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 594.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 19:20:03 | ||
图片预览






文档简介
(共18张PPT)
第9章 多边形 复习课件
小结与复习
目的
1.通过小结本章的知识结构,培养学生分析、归纳、总结的能力。
2.使学生体验三角形性质:三角形外角和、三角形的三边关系、多边形内角和、多边形外角和的探索过程,掌握三角形的性质,并会用它们进行有关计算。
3.使学生进一步理解某些正多边形能够铺满地面的道理。
4.理解三角形的三种重要线段——中线、角平分线和高的概念,并会画出这三种线段。
小结与复习
重点、难点
1.重点:三边关系、三角形的外角性质,多边形的外角和与内角和以及高的画法。
2.难点:灵活应用三角形的性质进行有关计算。
。
三角形用符号“△”加顶点字母表示.如顶点为A,B,C的三角形记作
“△ABC”。
从三角形的一个顶点向它的对边所在的直线作垂线,顶点与垂足之间的
线段叫做三角形的高。
连结三角形的顶点与它的对边中点的线段叫做三角形的中线。
角形的一个角的平分线与这个角的对边相交,这个角的顶点与交
点之间的线段叫做三角形的角平分线。
三角形的内角和等于180°
三角形的外角和等于360°
三角形的任何两边的和大于第三边。
三角形的一个外角等于与它不相邻的两个内角和;三角形
的一个外角大于任何一个与它不相邻的内角。
锐角三角形、直角三角形、钝角三角形
等腰三角形、不等边三角形
知识框架
由n条不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形。
n边形的内角和等于(n-2) 180°(n是大于或等于3的整数)。
多边形的外角和等于360°。
围绕一点拼在一起的几个内角加在一起恰
好能组成一个周角。
围绕在一点的几个正多边形的内角之和为一
个周角。
三角形的主要概念
边、顶点、内角、外角
三角形的三条主要线段——中线、角平分线、高。
三角形任意两边之和大于第三边,两边的差小于第三边。注意“任意”的含义。
三角形内角和等于180°,外角的两个性质,这是平面几何中很重要的一个基本性质。
三角形分类
按角可分为:锐角三角形、直角三角形和钝角三角形。
按边可分为:三边都不相等的三角形、等腰三角形两类,而等边三角形是等腰三角形的特例。
第9章 多边形
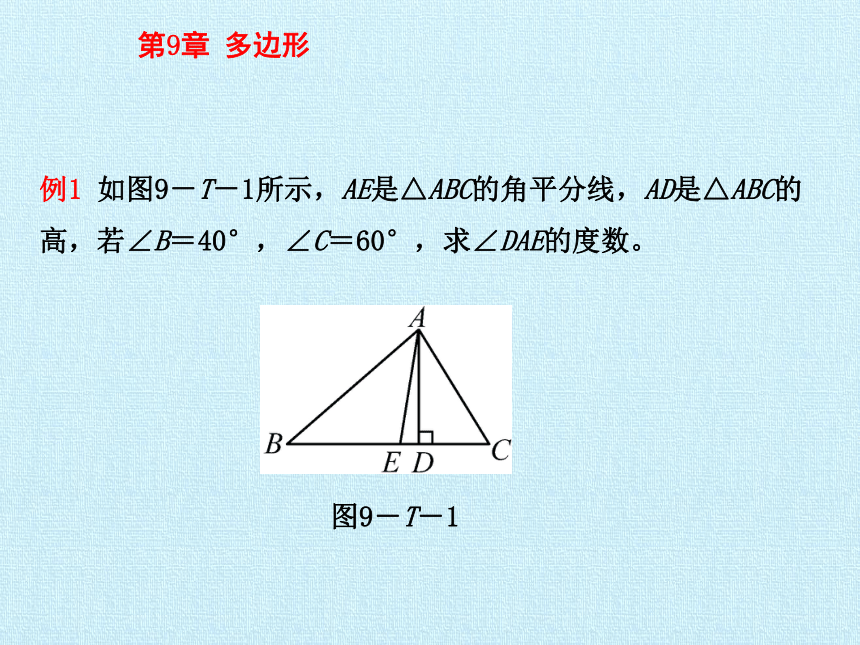
例1 如图9-T-1所示,AE是△ABC的角平分线,AD是△ABC的高,若∠B=40°,∠C=60°,求∠DAE的度数。
图9-T-1
第9章 多边形
三、巩固练习
选择题
1.在下列四组线段中,可以组成三角形的是( )
①1,2,3; ②4,5,6;③ 1,1/2,1/3;④15,72,90
A.1组 B.2组 C.3组 D.4组
A
2.下列四种说法正确的个数是( )
①一个三角形的三个内角中至多有一个钝角
②一个三角形的三个内角中至少有2个锐角
③一个三角形的三个内角中至少有一个直角
④一个三角形的三个外角中至少有两个钝角
A.1个 B.2个 C.3个 D.4个
∨
∨
×
×
B
三、巩固练习
选择题
3.△ABC中,三边长为6、7、x,则x的取值范围是( )
A.24.等腰三角形两边长分别是5和7,则该三角形周长为( )
A.17 B.19 C17或19 D.无法确定
B
C
问题2:△ABC的三边a、b、c都是正整数,且满足
0<a≤b≤c,如果b=4,问这样的三角形有多少个?
∵0<a≤4,且为正整数, ∴a=1,2,3,4
∵c≥4,∴有以下10种组合,可构成三角形。
a=1,b=4,c=4
a=2,b=4,c=4
a=2,b=4,c=5
a=3,b=4,c=4
a=3,b=4,c=5
a=3,b=4,c=6
a=4,b=4,c=4
a=4,b=4,c=5
a=4,b=4,c=6
a=4,b=4,c=7
问题3:如图(1)依图填空:
1.在△ABC中,BC边上的高是
( )
2.在△AEC中,AE边上的高是
( )
3.在△FEC中,EC边上的高是( )
4.AB=CD=2cm,AE=3cm ,则△AEC的面积S=( ),CE=( )
AB
CD
1/2×AE×CD=1/2CE×AB
3cm
E
FE
问题4:如图(2),在△ABC中,D是BC上一点,∠1=∠2,∠3=∠4,
∠BAC=63°求∠DAC的数。
解:设∠DAC=xo
∵∠BAC=∠1+∠DAC=63o
∴ ∠1+x=63o…………………………①
∵∠1=∠2,∠4=∠1+∠2
∴ ∠4=∠3=2 ∠1
∵∠DAC+∠3+∠4=180o
∴ x+2∠1+2∠1=180o
即 x+4∠1=180o ……………………②
联立解①②,可得:x=24o
∴ ∠DAC=24o
问题5:如图,在△ABC中,∠ABC与∠ACB的平分线相交于D,那么∠BDC=90o+1/2∠A。你会说明这个结论正确?
解:
∵△BDC中,∠1+∠BDC+∠2=180o
∴ ∠BDC=180o-(∠1+∠2)
∵BD、CD分别平分∠ABC和∠ACB
∴∠1=1/2∠ABC,∠2=1/2∠ACB
∴∠BDC=180o- 1/2(∠ABC+∠ACB)
∴∠ABC+∠ACB=180o-∠A
∵△ABC中,∠A+∠ABC+∠ACB=180o
∴∠BDC=180o- 1/2(180o-∠A)
∴∠BDC=90o+1/2∠A
第9章 多边形
类型之四 与多边形有关的计算
与多边形有关的计算一般是多边形内角和或外角和及它们的综合运用,近几年中考题目中都有铺设地面的问题,因为它与生活密切相连。
例6 若在一个拼接点周围用2个正方形和n个正三角形恰好可以铺满地面,则n的值是( )
A.3 B.4 C.5 D.6
A
[解析]用多个正多边形铺满地面的条件是围绕某一拼接点的几个角组成周角即可,所以360°=2×90°+60°×n,解得n=3。
问题7:已知多边形的一个内角的外角与其它各内角和为600°,求边数及相应的外角的度数。
解:设外角的度数为xo,则它的内角度数为(180-x)o
多边形的边数为n。
根据题意,得180-x+600o=(n-2)×180o
∵0o∴0<780o-(n-2)×180o<180o
解得:
∴x=780o-(n-2)×180o
∵n为正整数,∴n=6
∴x=780o-(6-2)×180o=60o
答:边数为6,外角的度数为60o
第9章 多边形
[解析] 由于多边形外角和为360°,所以可以列方程求解。
谢 谢
第9章 多边形 复习课件
小结与复习
目的
1.通过小结本章的知识结构,培养学生分析、归纳、总结的能力。
2.使学生体验三角形性质:三角形外角和、三角形的三边关系、多边形内角和、多边形外角和的探索过程,掌握三角形的性质,并会用它们进行有关计算。
3.使学生进一步理解某些正多边形能够铺满地面的道理。
4.理解三角形的三种重要线段——中线、角平分线和高的概念,并会画出这三种线段。
小结与复习
重点、难点
1.重点:三边关系、三角形的外角性质,多边形的外角和与内角和以及高的画法。
2.难点:灵活应用三角形的性质进行有关计算。
。
三角形用符号“△”加顶点字母表示.如顶点为A,B,C的三角形记作
“△ABC”。
从三角形的一个顶点向它的对边所在的直线作垂线,顶点与垂足之间的
线段叫做三角形的高。
连结三角形的顶点与它的对边中点的线段叫做三角形的中线。
角形的一个角的平分线与这个角的对边相交,这个角的顶点与交
点之间的线段叫做三角形的角平分线。
三角形的内角和等于180°
三角形的外角和等于360°
三角形的任何两边的和大于第三边。
三角形的一个外角等于与它不相邻的两个内角和;三角形
的一个外角大于任何一个与它不相邻的内角。
锐角三角形、直角三角形、钝角三角形
等腰三角形、不等边三角形
知识框架
由n条不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形。
n边形的内角和等于(n-2) 180°(n是大于或等于3的整数)。
多边形的外角和等于360°。
围绕一点拼在一起的几个内角加在一起恰
好能组成一个周角。
围绕在一点的几个正多边形的内角之和为一
个周角。
三角形的主要概念
边、顶点、内角、外角
三角形的三条主要线段——中线、角平分线、高。
三角形任意两边之和大于第三边,两边的差小于第三边。注意“任意”的含义。
三角形内角和等于180°,外角的两个性质,这是平面几何中很重要的一个基本性质。
三角形分类
按角可分为:锐角三角形、直角三角形和钝角三角形。
按边可分为:三边都不相等的三角形、等腰三角形两类,而等边三角形是等腰三角形的特例。
第9章 多边形
例1 如图9-T-1所示,AE是△ABC的角平分线,AD是△ABC的高,若∠B=40°,∠C=60°,求∠DAE的度数。
图9-T-1
第9章 多边形
三、巩固练习
选择题
1.在下列四组线段中,可以组成三角形的是( )
①1,2,3; ②4,5,6;③ 1,1/2,1/3;④15,72,90
A.1组 B.2组 C.3组 D.4组
A
2.下列四种说法正确的个数是( )
①一个三角形的三个内角中至多有一个钝角
②一个三角形的三个内角中至少有2个锐角
③一个三角形的三个内角中至少有一个直角
④一个三角形的三个外角中至少有两个钝角
A.1个 B.2个 C.3个 D.4个
∨
∨
×
×
B
三、巩固练习
选择题
3.△ABC中,三边长为6、7、x,则x的取值范围是( )
A.2
A.17 B.19 C17或19 D.无法确定
B
C
问题2:△ABC的三边a、b、c都是正整数,且满足
0<a≤b≤c,如果b=4,问这样的三角形有多少个?
∵0<a≤4,且为正整数, ∴a=1,2,3,4
∵c≥4,∴有以下10种组合,可构成三角形。
a=1,b=4,c=4
a=2,b=4,c=4
a=2,b=4,c=5
a=3,b=4,c=4
a=3,b=4,c=5
a=3,b=4,c=6
a=4,b=4,c=4
a=4,b=4,c=5
a=4,b=4,c=6
a=4,b=4,c=7
问题3:如图(1)依图填空:
1.在△ABC中,BC边上的高是
( )
2.在△AEC中,AE边上的高是
( )
3.在△FEC中,EC边上的高是( )
4.AB=CD=2cm,AE=3cm ,则△AEC的面积S=( ),CE=( )
AB
CD
1/2×AE×CD=1/2CE×AB
3cm
E
FE
问题4:如图(2),在△ABC中,D是BC上一点,∠1=∠2,∠3=∠4,
∠BAC=63°求∠DAC的数。
解:设∠DAC=xo
∵∠BAC=∠1+∠DAC=63o
∴ ∠1+x=63o…………………………①
∵∠1=∠2,∠4=∠1+∠2
∴ ∠4=∠3=2 ∠1
∵∠DAC+∠3+∠4=180o
∴ x+2∠1+2∠1=180o
即 x+4∠1=180o ……………………②
联立解①②,可得:x=24o
∴ ∠DAC=24o
问题5:如图,在△ABC中,∠ABC与∠ACB的平分线相交于D,那么∠BDC=90o+1/2∠A。你会说明这个结论正确?
解:
∵△BDC中,∠1+∠BDC+∠2=180o
∴ ∠BDC=180o-(∠1+∠2)
∵BD、CD分别平分∠ABC和∠ACB
∴∠1=1/2∠ABC,∠2=1/2∠ACB
∴∠BDC=180o- 1/2(∠ABC+∠ACB)
∴∠ABC+∠ACB=180o-∠A
∵△ABC中,∠A+∠ABC+∠ACB=180o
∴∠BDC=180o- 1/2(180o-∠A)
∴∠BDC=90o+1/2∠A
第9章 多边形
类型之四 与多边形有关的计算
与多边形有关的计算一般是多边形内角和或外角和及它们的综合运用,近几年中考题目中都有铺设地面的问题,因为它与生活密切相连。
例6 若在一个拼接点周围用2个正方形和n个正三角形恰好可以铺满地面,则n的值是( )
A.3 B.4 C.5 D.6
A
[解析]用多个正多边形铺满地面的条件是围绕某一拼接点的几个角组成周角即可,所以360°=2×90°+60°×n,解得n=3。
问题7:已知多边形的一个内角的外角与其它各内角和为600°,求边数及相应的外角的度数。
解:设外角的度数为xo,则它的内角度数为(180-x)o
多边形的边数为n。
根据题意,得180-x+600o=(n-2)×180o
∵0o
解得:
∴x=780o-(n-2)×180o
∵n为正整数,∴n=6
∴x=780o-(6-2)×180o=60o
答:边数为6,外角的度数为60o
第9章 多边形
[解析] 由于多边形外角和为360°,所以可以列方程求解。
谢 谢
