华东师大版七年级下册数学 8.2.2 不等式的简单变形(1) 课件 (共23张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 8.2.2 不等式的简单变形(1) 课件 (共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
8.2不等式的简单变形
华东师大版数学七年级下册
一、督预示标
1.你能用适当的不等式表示下列的 关系吗?
⑴X+1是负数;
⑵ 是非负数;
⑶X与17的和比5小。
a
2
X+1<0
a ≥ 0
2
X +17<5
2.等式的基本性质是什么?
温故知新
等式性质1:等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式。
等式性质2:等式两边都乘以(或除以)同一个数(除数不能是0),所得结果仍是等式。
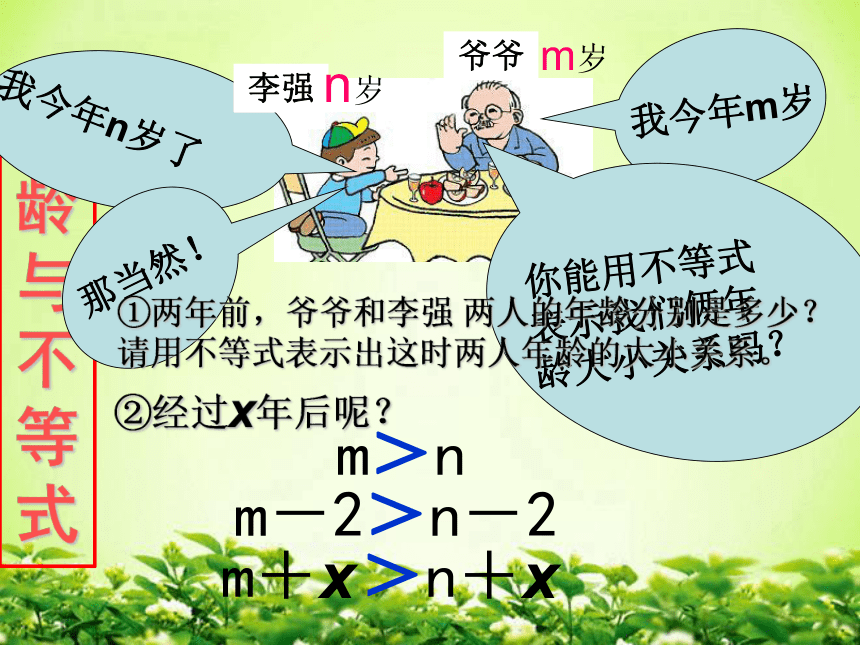
年龄与不等式
我今年m岁
我今年n岁了
你能用不等式
表示我们俩年
龄大小关系吗?
那当然!
m>n
①两年前,爷爷和李强 两人的年龄分别是多少?请用不等式表示出这时两人年龄的大小关系。
②经过x年后呢?
m-2>n-2
m+x >n+x
李强
爷爷
m岁
n岁
学习目标:
1、掌握不等式的基本性质1,2,3
2、运用不等式的三个性质对不等
式变形。
2、(1)观察:用“<”或“>”填空,并找一找其中的规律.
(2) 6>2, 6×5____2×5 , 6×(-5)____2×(-5) ;
(3) –2<3, (-2)×6____3×6 , (-2)×(-6)____3×(-6)
5>3, 5+2____3+2 , 5-2____3-2 ;
>
>
>
<
<
>
(2)思考: 1、不等式性质1、2分别是什么?
2、不等式性质3是什么?
3、等式性质与不等式性质有什么相 同与不同之处?
4、怎样解不等式?
二、自学梳理:
1、请学生自学课本第55——57页。
待自主学习完成以后,各小组由组长主持、小组成员合作学习,完成以下程序:
1、让每个组员将自己的学习成果讲给其他同学听。
2、把在自学的过程中遇到的问题,在小组内讨论交流。
3、对照学习目标和自学提纲,推选好准备在全班进行学习成果展示的问题和同学。
三、小组答疑:
新课探究
根据不等式 7 > 4 填空:
7×(-3)__ 4×(-3)
7×(-2)__ 4 ×(-2)
7×(-1)__ 4×(-1)
<
<
<
四、展示评价1 不等式性质
【不等式性质1】
不等式的两边都加上或减去同一个数或
同一个整式,不等号的方向不变.
【不等式性质2】
不等式的两边都乘以(或除以)同一个正数,
不等号的方向不变.
【不等式性质3】
不等式的两边都乘以(或除以)同一个负数,
不等号的方向改变.
新课探究
根据不等式 7 > 4 填空:
7×(-3)__ 4×(-3)
7×(-2)__ 4 ×(-2)
7×(-1)__ 4×(-1)
<
<
<
对比等式与不等式的性质
两边都加上或减去同一个数或同一个整式
两边都乘以或除以同一个正数
两边都乘以或除以同一个负数
变形
关系式
等式
不等式
仍成立
仍成立
仍成立
仍成立
仍成立
不等号方向改变才成立
展示评价2 看谁答的又快又准
练习1:已知 m>n 用”>”或”<”填空
(1)m-5____n-5
(2)m+4____n+4
(3)16m____16n
(4)-3m____-3n
>
>
>
<
———不等式性质1
———不等式性质1
———不等式性质3
———不等式性质2
加减都用性质1.不等号方向不改变。
乘除正数性质2.不等号方向还不变。
乘除负数性质3.不等号方向必改变。
巧 记 口 决
2.已知x>y,下列不等式成立吗?并说明理由。
⑴x-6<y-6
⑶-2x<-2y
⑵3x<3y
⑷x-y>0
解:⑴不成立。理由:根据不等式
基本性质1 两边都减去6,得
x-6>y-6
解:⑵不成立。理由:根据不等式
基本性质2 两边都乘以3,得
3x>3y
解:⑷成立。理由:根据不等式
基本性质1 两边都减去y,得
X-y>0
解:⑶成立。理由:根据不等式
基本性质3 两边都乘以-2,得
-2X<-2y
能力提高
3.真真假假我来辨
⑴由-2a>3,得a >-
⑵由2-a<0,得2<a
⑶由a<b得a+m<b+m
⑷由3<4得3a<4a
3
2
(√ )
(√ )
(×)
(×)
新课探究
根据不等式 7 > 4 填空:
7×(-3)__ 4×(-3)
7×(-2)__ 4 ×(-2)
7×(-1)__ 4×(-1)
<
<
<
展示评价3 怎样解不等式呢
不等式
变形
x >a
x≥a
xx≤a
x≠a
最简形式
新课探究
根据不等式 7 > 4 填空:
7×(-3)__ 4×(-3)
7×(-2)__ 4 ×(-2)
7×(-1)__ 4×(-1)
<
<
<
(2) 3x<2x-3
解:不等式的两边都减去2x,不等号的方向不变,所以
3x-2x﹤2x-3-2x
(1)x-7<8
解:不等式的两边都加上7,不等号的方向不变,所以
x-7+7<8+7
例题示范
这两个小题中不等式的变形与解方程的哪个步骤类似?
例1、解不等式
x﹤15
x﹤-3
移项的依据是什么
移项要注意什么
思考
新课探究
根据不等式 7 > 4 填空:
7×(-3)__ 4×(-3)
7×(-2)__ 4 ×(-2)
7×(-1)__ 4×(-1)
<
<
<
解下列不等式,并将其解集表示在数轴上
(1) x-2>0 (2) x+1≥0
解:(1)移项,得
x>2
1
2
4
5
6
3
0
解:(2)移项,得
x≥-1
-2
-1
1
2
3
0
-3
巩固练习
新课探究
根据不等式 7 > 4 填空:
7×(-3)__ 4×(-3)
7×(-2)__ 4 ×(-2)
7×(-1)__ 4×(-1)
<
<
<
例2、解不等式
(1) X > -3 (2) -2x < 6
解:(1)两边同时乘以2,不等号的方向不变,所以
解:(2)两边同时除以-2,不等号的方向改变,所以
系数化为1的依据是什么
系数化为1时要注意什么
思考
例题示范
这两个小题中不等式的变形与解方程的哪个步骤类似?
X > -6
X > -3
新课探究
根据不等式 7 > 4 填空:
7×(-3)__ 4×(-3)
7×(-2)__ 4 ×(-2)
7×(-1)__ 4×(-1)
<
<
<
巩固练习
解不等式并将其解集表示在数轴上
(1)-2x < 4 (2) 3x ≤ 0
-2
-1
1
2
3
0
-3
解:(1) 系数化为1,得
解:(2) 系数化为1,得
-2
-1
1
2
3
0
-3
X ≤ 0
X > -2
1、若ac2 ≤ ac2,则a b;若a︱c︳>b︱c︳, a b;
2、a/c>b/c,若c>0,则a b,若c<0,则a b;
3、已知a<0,-1<b<0,试比较a,ab,ab2之间的大小关系。
五、联系拓展
≤
>
>
<
a <ab2 <ab
六、总结导预 凯旋归来话收获
探究不等式的三条性质
不等式性质1 不等式的两边都加上(或减去)同 一个数或同一个整式,不等号的方向不变。
不等式性质2 不等式的两边都乘以(或除以)同 一个正数,不等号的方向不变。
不等式性质3 不等式的两边都乘以(或除以)同 个负数,不等号的方向改变。
作 业
课本习题8.2的1、2题。
自学教材:第58——60页内容,第61 习题。
尝试完成《学习检测》第55——56页习题。
自负≠自信
巧干 > 苦干
昨天<今天
研究≥经验
模仿≤原创
8.2不等式的简单变形
华东师大版数学七年级下册
一、督预示标
1.你能用适当的不等式表示下列的 关系吗?
⑴X+1是负数;
⑵ 是非负数;
⑶X与17的和比5小。
a
2
X+1<0
a ≥ 0
2
X +17<5
2.等式的基本性质是什么?
温故知新
等式性质1:等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式。
等式性质2:等式两边都乘以(或除以)同一个数(除数不能是0),所得结果仍是等式。
年龄与不等式
我今年m岁
我今年n岁了
你能用不等式
表示我们俩年
龄大小关系吗?
那当然!
m>n
①两年前,爷爷和李强 两人的年龄分别是多少?请用不等式表示出这时两人年龄的大小关系。
②经过x年后呢?
m-2>n-2
m+x >n+x
李强
爷爷
m岁
n岁
学习目标:
1、掌握不等式的基本性质1,2,3
2、运用不等式的三个性质对不等
式变形。
2、(1)观察:用“<”或“>”填空,并找一找其中的规律.
(2) 6>2, 6×5____2×5 , 6×(-5)____2×(-5) ;
(3) –2<3, (-2)×6____3×6 , (-2)×(-6)____3×(-6)
5>3, 5+2____3+2 , 5-2____3-2 ;
>
>
>
<
<
>
(2)思考: 1、不等式性质1、2分别是什么?
2、不等式性质3是什么?
3、等式性质与不等式性质有什么相 同与不同之处?
4、怎样解不等式?
二、自学梳理:
1、请学生自学课本第55——57页。
待自主学习完成以后,各小组由组长主持、小组成员合作学习,完成以下程序:
1、让每个组员将自己的学习成果讲给其他同学听。
2、把在自学的过程中遇到的问题,在小组内讨论交流。
3、对照学习目标和自学提纲,推选好准备在全班进行学习成果展示的问题和同学。
三、小组答疑:
新课探究
根据不等式 7 > 4 填空:
7×(-3)__ 4×(-3)
7×(-2)__ 4 ×(-2)
7×(-1)__ 4×(-1)
<
<
<
四、展示评价1 不等式性质
【不等式性质1】
不等式的两边都加上或减去同一个数或
同一个整式,不等号的方向不变.
【不等式性质2】
不等式的两边都乘以(或除以)同一个正数,
不等号的方向不变.
【不等式性质3】
不等式的两边都乘以(或除以)同一个负数,
不等号的方向改变.
新课探究
根据不等式 7 > 4 填空:
7×(-3)__ 4×(-3)
7×(-2)__ 4 ×(-2)
7×(-1)__ 4×(-1)
<
<
<
对比等式与不等式的性质
两边都加上或减去同一个数或同一个整式
两边都乘以或除以同一个正数
两边都乘以或除以同一个负数
变形
关系式
等式
不等式
仍成立
仍成立
仍成立
仍成立
仍成立
不等号方向改变才成立
展示评价2 看谁答的又快又准
练习1:已知 m>n 用”>”或”<”填空
(1)m-5____n-5
(2)m+4____n+4
(3)16m____16n
(4)-3m____-3n
>
>
>
<
———不等式性质1
———不等式性质1
———不等式性质3
———不等式性质2
加减都用性质1.不等号方向不改变。
乘除正数性质2.不等号方向还不变。
乘除负数性质3.不等号方向必改变。
巧 记 口 决
2.已知x>y,下列不等式成立吗?并说明理由。
⑴x-6<y-6
⑶-2x<-2y
⑵3x<3y
⑷x-y>0
解:⑴不成立。理由:根据不等式
基本性质1 两边都减去6,得
x-6>y-6
解:⑵不成立。理由:根据不等式
基本性质2 两边都乘以3,得
3x>3y
解:⑷成立。理由:根据不等式
基本性质1 两边都减去y,得
X-y>0
解:⑶成立。理由:根据不等式
基本性质3 两边都乘以-2,得
-2X<-2y
能力提高
3.真真假假我来辨
⑴由-2a>3,得a >-
⑵由2-a<0,得2<a
⑶由a<b得a+m<b+m
⑷由3<4得3a<4a
3
2
(√ )
(√ )
(×)
(×)
新课探究
根据不等式 7 > 4 填空:
7×(-3)__ 4×(-3)
7×(-2)__ 4 ×(-2)
7×(-1)__ 4×(-1)
<
<
<
展示评价3 怎样解不等式呢
不等式
变形
x >a
x≥a
x
x≠a
最简形式
新课探究
根据不等式 7 > 4 填空:
7×(-3)__ 4×(-3)
7×(-2)__ 4 ×(-2)
7×(-1)__ 4×(-1)
<
<
<
(2) 3x<2x-3
解:不等式的两边都减去2x,不等号的方向不变,所以
3x-2x﹤2x-3-2x
(1)x-7<8
解:不等式的两边都加上7,不等号的方向不变,所以
x-7+7<8+7
例题示范
这两个小题中不等式的变形与解方程的哪个步骤类似?
例1、解不等式
x﹤15
x﹤-3
移项的依据是什么
移项要注意什么
思考
新课探究
根据不等式 7 > 4 填空:
7×(-3)__ 4×(-3)
7×(-2)__ 4 ×(-2)
7×(-1)__ 4×(-1)
<
<
<
解下列不等式,并将其解集表示在数轴上
(1) x-2>0 (2) x+1≥0
解:(1)移项,得
x>2
1
2
4
5
6
3
0
解:(2)移项,得
x≥-1
-2
-1
1
2
3
0
-3
巩固练习
新课探究
根据不等式 7 > 4 填空:
7×(-3)__ 4×(-3)
7×(-2)__ 4 ×(-2)
7×(-1)__ 4×(-1)
<
<
<
例2、解不等式
(1) X > -3 (2) -2x < 6
解:(1)两边同时乘以2,不等号的方向不变,所以
解:(2)两边同时除以-2,不等号的方向改变,所以
系数化为1的依据是什么
系数化为1时要注意什么
思考
例题示范
这两个小题中不等式的变形与解方程的哪个步骤类似?
X > -6
X > -3
新课探究
根据不等式 7 > 4 填空:
7×(-3)__ 4×(-3)
7×(-2)__ 4 ×(-2)
7×(-1)__ 4×(-1)
<
<
<
巩固练习
解不等式并将其解集表示在数轴上
(1)-2x < 4 (2) 3x ≤ 0
-2
-1
1
2
3
0
-3
解:(1) 系数化为1,得
解:(2) 系数化为1,得
-2
-1
1
2
3
0
-3
X ≤ 0
X > -2
1、若ac2 ≤ ac2,则a b;若a︱c︳>b︱c︳, a b;
2、a/c>b/c,若c>0,则a b,若c<0,则a b;
3、已知a<0,-1<b<0,试比较a,ab,ab2之间的大小关系。
五、联系拓展
≤
>
>
<
a <ab2 <ab
六、总结导预 凯旋归来话收获
探究不等式的三条性质
不等式性质1 不等式的两边都加上(或减去)同 一个数或同一个整式,不等号的方向不变。
不等式性质2 不等式的两边都乘以(或除以)同 一个正数,不等号的方向不变。
不等式性质3 不等式的两边都乘以(或除以)同 个负数,不等号的方向改变。
作 业
课本习题8.2的1、2题。
自学教材:第58——60页内容,第61 习题。
尝试完成《学习检测》第55——56页习题。
自负≠自信
巧干 > 苦干
昨天<今天
研究≥经验
模仿≤原创
