华东师大版七年级下册数学 8.3 一元一次不等式组 课件(共22张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 8.3 一元一次不等式组 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 450.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 19:42:35 | ||
图片预览






文档简介
(共22张PPT)
8.3 一元一次不等式组
问题:
用每分钟抽30吨水的抽水机来抽污水管道积存的污水,估计积存的污水超过1200吨而不足1500吨,那么将污水抽完所用的时间的范围是什么?
解:设用x分钟将污水抽完,则x满足
类似于方程组的概念,你能说出一元一次不等式组的概念吗?
能用你学过的知识分析一下吗?
3x>1200 (1)
3x<1500 (2)
注意:
(1)每个不等式必须为一元一次不等式;
(2)不等式必须是只含有同一个未知数;
(3)不等式的数量是两个或者多个。
类似于方程组,把两个或两个以上含有相同未知数的一元一次不等式合起来,就组成一个一元一次不等式组。
下列各式中,哪些是一元一次不等式组?
√
×
√
×
×
×
观察与思考
如何解此不等式组呢?
分析
类比方程组的解,怎样确定不等式组中X的取值范围呢?
不等式组中的各不等式解集的公共部分,
就是不等式组中X的取值范围
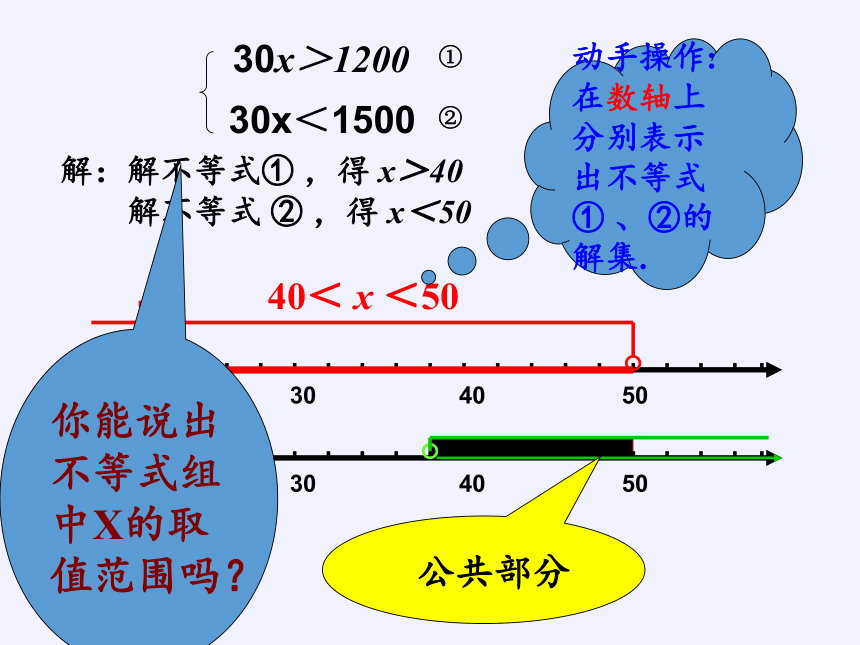
30x>1200 (1)
30x<1500 (2)
30
20
40
50
30
20
40
50
30x<1500
30x>1200
①
②
解:解不等式① ,得 x>40
解不等式 ② ,得 x<50
∴ 40< x <50
公共部分
动手操作:在数轴上分别表示出不等式① 、②的解集.
你能说出不等式组中X的取值范围吗?
几个不等式的解集的公共部分叫做这个不等式组的解集。
解不等式组就是求它的解集。
议一议
什么叫做不等式组的解集
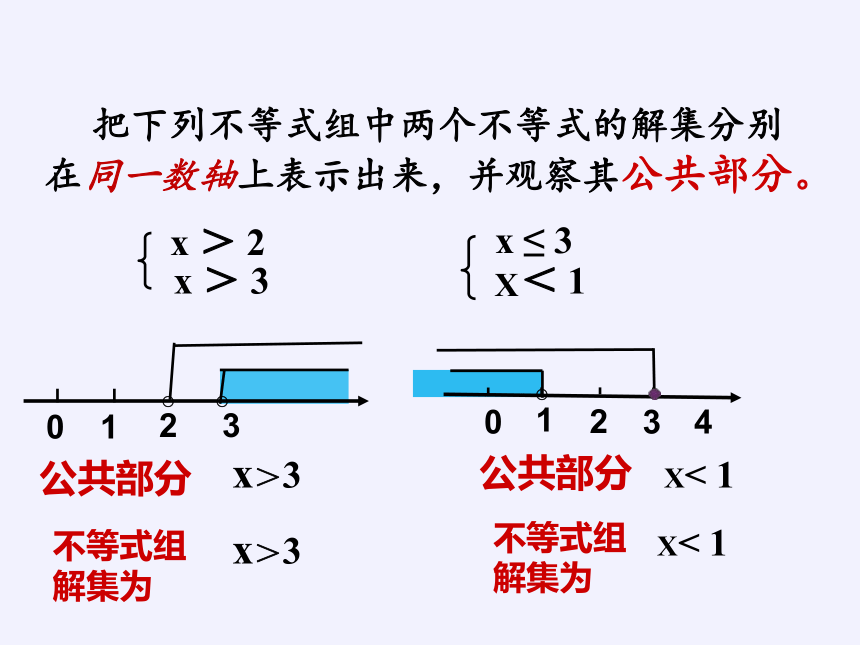
把下列不等式组中两个不等式的解集分别在同一数轴上表示出来,并观察其公共部分。
x > 2
x > 3
x ≤ 3
X
<
1
公共部分
x>3
X< 1
公共部分
3
0
4
○
2
1
○
○
2
3
0
1
不等式组解集为
x>3
X< 1
不等式组解集为
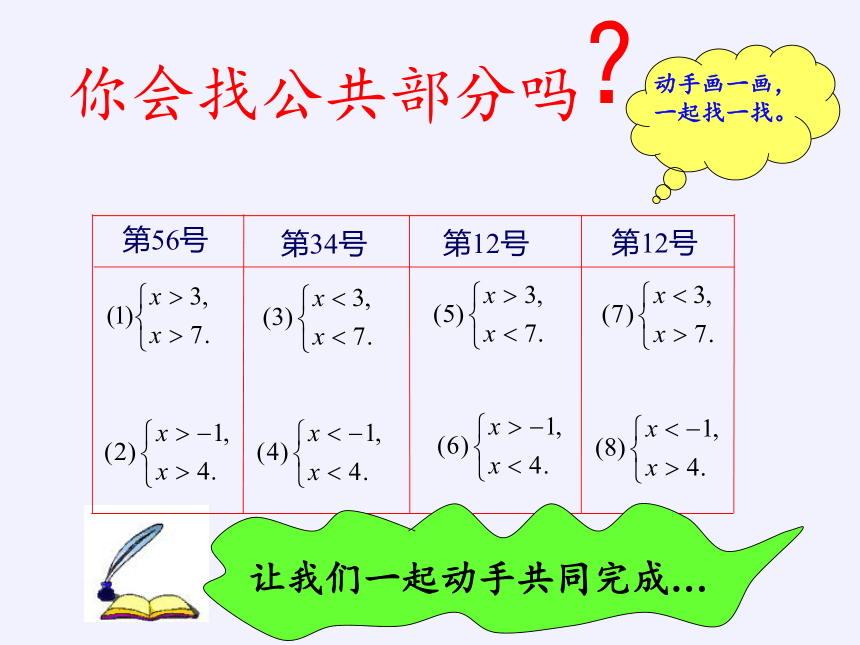
第56号
第34号
第12号
第12号
?
你会找公共部分吗
动手画一画,一起找一找。
让我们一起动手共同完成…
求下列不等式组的解集:(第5、6号)
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为
解:原不等式组的解集为
-3
-2
-1
0
4
2
1
3
5
-3
-2
-1
0
4
2
1
3
5
求下列不等式组的解集:(第3、4号)
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为
解:原不等式组的解集为
求下列不等式组的解集:(第1、2号)
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:原不等式组的解集为
解:原不等式组的解集为
求下列不等式组的解集:(第1、2号)
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:原不等式组无解.
解:原不等式组无解.
a
a
a
b
x>a
x> b
x<a
x<b
x<a
x> b
x>a x<b
。
。
a
。
。
b
。
。
b
。
。
b
解集为 : x> b
解集为 : x<a
一元一次不等式组的解集的规律图析
(若当 a<b时 )
解集为: a<x<b
解集为:无解
同大取大
同小取小
大小小大中间找
大大小小全不要
0 2 3
你会了吗 试试看
例1:解下列不等式组
解: 解不等式①得:
解不等式②得:
把不等式①和 ②的解集在数轴上表示出来:
②
①
∴不等式组的解集为
议一议:
解一元一次不等式组的解题步骤:
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的 公共部分;
(3)根据几个不等式解集的公共部分,写出 这个不等式组的解集。
根据上题的解答过程你认为解一元一次不等式组的一般步骤是什么
0
8
②
①
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
∴不等式组无解。
比一比,看谁又快又好
1. 由几个含有相同未知数的一元一次不等式所组成的不等式组叫做一元一次不等式组 .
2. 几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集.
3. 求不等式组的解集的过程,叫做解不等式组.
(二)解简单一元一次不等式组的方法:
(1)
求出不等式组中各个不等式的解集
(2) 利用数轴找出这几个不等式解集的公共部分
(3)根据几个不等式解集的公共部分,写出这个不等式组的解集。
(一)概念
(找不到公共部分则不等式组无解)
本节知识回顾
同大取大
同小取小
大小小大中间找
大大小小全不要
(三)找不等式组公共部分的口诀:
感受数学思想
1、与方程组的类比引入不等式组。
2、利用数轴直观地表示不等式组的解集。
类比思想
数形结合思想
布置作业
课本:64页练习
65页练习、习题
写数学本上
谢 谢
8.3 一元一次不等式组
问题:
用每分钟抽30吨水的抽水机来抽污水管道积存的污水,估计积存的污水超过1200吨而不足1500吨,那么将污水抽完所用的时间的范围是什么?
解:设用x分钟将污水抽完,则x满足
类似于方程组的概念,你能说出一元一次不等式组的概念吗?
能用你学过的知识分析一下吗?
3x>1200 (1)
3x<1500 (2)
注意:
(1)每个不等式必须为一元一次不等式;
(2)不等式必须是只含有同一个未知数;
(3)不等式的数量是两个或者多个。
类似于方程组,把两个或两个以上含有相同未知数的一元一次不等式合起来,就组成一个一元一次不等式组。
下列各式中,哪些是一元一次不等式组?
√
×
√
×
×
×
观察与思考
如何解此不等式组呢?
分析
类比方程组的解,怎样确定不等式组中X的取值范围呢?
不等式组中的各不等式解集的公共部分,
就是不等式组中X的取值范围
30x>1200 (1)
30x<1500 (2)
30
20
40
50
30
20
40
50
30x<1500
30x>1200
①
②
解:解不等式① ,得 x>40
解不等式 ② ,得 x<50
∴ 40< x <50
公共部分
动手操作:在数轴上分别表示出不等式① 、②的解集.
你能说出不等式组中X的取值范围吗?
几个不等式的解集的公共部分叫做这个不等式组的解集。
解不等式组就是求它的解集。
议一议
什么叫做不等式组的解集
把下列不等式组中两个不等式的解集分别在同一数轴上表示出来,并观察其公共部分。
x > 2
x > 3
x ≤ 3
X
<
1
公共部分
x>3
X< 1
公共部分
3
0
4
○
2
1
○
○
2
3
0
1
不等式组解集为
x>3
X< 1
不等式组解集为
第56号
第34号
第12号
第12号
?
你会找公共部分吗
动手画一画,一起找一找。
让我们一起动手共同完成…
求下列不等式组的解集:(第5、6号)
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为
解:原不等式组的解集为
-3
-2
-1
0
4
2
1
3
5
-3
-2
-1
0
4
2
1
3
5
求下列不等式组的解集:(第3、4号)
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为
解:原不等式组的解集为
求下列不等式组的解集:(第1、2号)
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:原不等式组的解集为
解:原不等式组的解集为
求下列不等式组的解集:(第1、2号)
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:原不等式组无解.
解:原不等式组无解.
a
a
a
b
x>a
x> b
x<a
x<b
x<a
x> b
x>a x<b
。
。
a
。
。
b
。
。
b
。
。
b
解集为 : x> b
解集为 : x<a
一元一次不等式组的解集的规律图析
(若当 a<b时 )
解集为: a<x<b
解集为:无解
同大取大
同小取小
大小小大中间找
大大小小全不要
0 2 3
你会了吗 试试看
例1:解下列不等式组
解: 解不等式①得:
解不等式②得:
把不等式①和 ②的解集在数轴上表示出来:
②
①
∴不等式组的解集为
议一议:
解一元一次不等式组的解题步骤:
(1)求出不等式组中各个不等式的解集;
(2)利用数轴,找出这些不等式解集的 公共部分;
(3)根据几个不等式解集的公共部分,写出 这个不等式组的解集。
根据上题的解答过程你认为解一元一次不等式组的一般步骤是什么
0
8
②
①
解: 解不等式①,得,
解不等式②,得,
把不等式①和 ②的解集在数轴上表示出来:
∴不等式组无解。
比一比,看谁又快又好
1. 由几个含有相同未知数的一元一次不等式所组成的不等式组叫做一元一次不等式组 .
2. 几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集.
3. 求不等式组的解集的过程,叫做解不等式组.
(二)解简单一元一次不等式组的方法:
(1)
求出不等式组中各个不等式的解集
(2) 利用数轴找出这几个不等式解集的公共部分
(3)根据几个不等式解集的公共部分,写出这个不等式组的解集。
(一)概念
(找不到公共部分则不等式组无解)
本节知识回顾
同大取大
同小取小
大小小大中间找
大大小小全不要
(三)找不等式组公共部分的口诀:
感受数学思想
1、与方程组的类比引入不等式组。
2、利用数轴直观地表示不等式组的解集。
类比思想
数形结合思想
布置作业
课本:64页练习
65页练习、习题
写数学本上
谢 谢
