华东师大版七年级下册数学第7章一次方程组复习课件 (共26张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学第7章一次方程组复习课件 (共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 387.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
第7章 一次方程组 复习课件
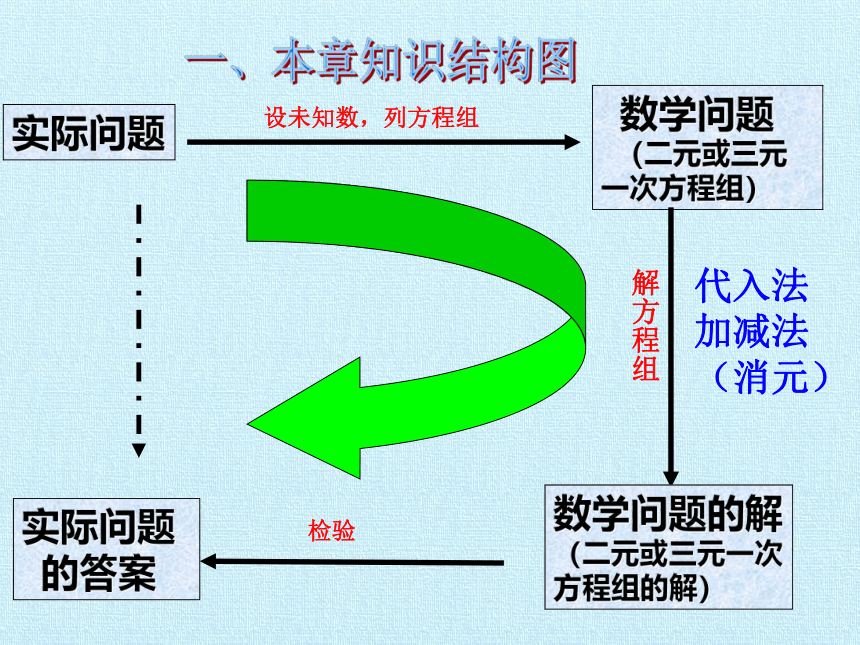
实际问题
设未知数,列方程组
数学问题
(二元或三元一次方程组)
解方程组
数学问题的解
(二元或三元一次
方程组的解)
检验
实际问题
的答案
一、本章知识结构图
代入法
加减法
(消元)
二、有关概念
1.二元一次方程:通过化简后,只有两个未知数,并且两个未知数的次数都是1,系数都不是0的整式方程,叫做二元一次方程。
2.二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解。
3.二元一次方程组:由两个一次方程组成,共有两个未知数的方程组,叫做二元一次方程组。
4.二元一次方程组的解:使二元一次方程组的两个方程左、右两边的值都相等的两个未知数的值,叫做二元一次方程组的解。
三、方程组的解法
根据方程未知数的系数特征确定用哪一种解法。
基本思想或思路——消元
常用方法——代入法和加减法
用代入法解二元一次方程组的步骤:
1.求表达式:从方程组中选一个系数比较简
单的方程,将此方程中的一个未知数,如y,用
含x的代数式表示;
2.把这个含x的代数式代入另一个方程中,
消去y,得到一个关于x的一元一次方程;
3.解一元一次方程,求出x的值;
4.再把求出的x的值 代入变形后的方程,求
出y的值。
用加减法解二元一次方程组的步骤:
1.利用等式性质把一个或两个方程的两边都
乘以适当的数,变换两个方程的某一个未知数
的系数,使其绝对值相等;
2.把变换系数后的两个方程的两边分别相加或相减,消去一个未知数,得一元一次方程;
3.解这个一元一次方程,求得一个未知数的值 ;
4.把所求的这个未知的值代入方程组中较为简便的一个方程,求出另一个未知数,从而得到方程的解。
解三元一次方程组的基本思路与解二元一次方程组的基本思路一样,即:
三元一次方程组
消元
二元一次方程组
消元
一元一次方程
三元一次方程组的解法
应用题:
列方程组解应用题的一般步骤:
1.审 2.设 3.列 4.解 5.答
一、行程问题:
1.相遇问题:甲的路程+乙的路程=总的路程
(环形跑道):甲的路程+乙的路程=一圈长
2.追及问题:快者的路程-慢者的路程
=原来相距路程
(环形跑道): 快者的路程-慢者的路程=一圈长
3.顺逆问题:顺速=静速+水(风)速
逆速=静速-水(风)速
例1 A、B两地相距36千米。甲从A地出发步行到B地,乙从B地出发步行到A地。两人同时出发,4小时相遇,6小时后,甲所余路程为乙所余路程的2倍,求两人的速度。
解:设甲、乙的速度分别为x千米/小时和y千米/小时。
依题意可得:
解得
答:甲、乙的速度分别为4千米/小时和5千米/小时。
例2 某人要在规定的时间内由甲地赶往乙地,如果他以每小时50千米的速度行驶,就会迟到24分钟,如果他以每小时75千米的速度行驶,就会提前24分钟 到达乙地,求甲、乙两地间的距离。
、
例3 甲、乙二人以不变的速度在环形路上跑步,如果同时同地出发,相向而行,每隔2分钟相遇一次;如果同向而行,每隔6分钟相遇一次。已知甲比乙跑得快,甲、乙每分钟各跑多少圈?
1.某学校现有甲种材料35㎏,乙种材料29㎏,制作A、B两种型号的工艺品,用料情况如下表:
需甲种材料 需乙种材料
1件A型工艺品 0.9㎏ 0.3㎏
1件B型工艺品 0.4㎏ 1㎏
(1)利用这些材料能制作A、B两种工艺品各多少件?
(2)若每公斤甲、乙种材料分别为8元和10元,问制作A、B两种型号的工艺品各需材料多少钱?
二、图表问题
2.某种植大户计划安排10个劳动力来耕作30亩土地,这些土地可以种蔬菜也可以种水稻,种这些作物所需劳动力及预计产值如下表:
每亩所需劳动力(个) 每亩预计产值(元)
蔬菜 3000
水稻 700
(1)为了使所有土地种上作物,全部劳动力都有工作,应安排种蔬菜的劳动力多少人?
(2)这时预计产值是多少?
3. 下表是某一周甲、乙两种股票的收盘价(股票每天交易结束时的价格)
星期一 星期二
甲 12
乙 13.5
张师傅在该周内持有若干甲、乙两种股票,若按照两种股票每天收盘价计算(不计手续费、税费行等),该人账户中星期二比星期一多获利200元,星期三比星期二多获利1300元,试问张师傅持有甲、乙股票各多少股?
12.5
13.3
星期三
星期四
星期五
星期六
12.9
13.9
12.45
13.4
12.75
13.15
休盘
休盘
解:设张师傅持有甲种股票x股,乙种股票y
股,根据题意,得:
解得
答:张师傅持有甲种股票1000股,乙种股票
1500股。
1.入世后,国内各汽车企业展开价格大战,汽车价格大幅下降,有些型号的汽车供不应求。某汽车生产厂接受了一份订单,要在规定的日期内生产一批汽车,如果每天生产35辆,则差10辆完成任务,如果每天生产40辆,则可提前半天完成任务,问订单要多少辆汽车,规定日期是多少天?
三.总量不变问题
四.销售问题:
标价×折扣=售价
售价—进价=利润
利润率=
达标检测
1.22名工人按定额完成了1400件产品,其中三级工每人定额200件,二级工每人定额50件。若这22名工人中只有二级工与三级工,问二级工与三级工各有多少名?
解:设二级工x名,三级工y名。
根据题意得:
x+y=22
50x
+200y
=1400
解得:
经检验,符合题意。
答:二级工20名,三级工2名。
2.有一批机器零件共418个,若甲先做2天,乙再加入合作,则再做2天可超产2个,若乙先做3天,然后两人再共做2天,则还有8个未完成。问甲、乙两人每天各做多少个零件?
根据题意得:
2x
3y
+2(x+y)
=418
解得:
答:甲每天做80个零件,乙每天做50个零件。
解:甲每天做x个零件,乙每天做y个零件。
经检验,符合题意
+2(x+y)
-2
=418
+8
3.为改善富春河的周围环境,县政府决定,将该河上游A地的一部分牧场改为林场。改变后,预计林场和牧场共有162公顷,牧场面积是林场面积的20%。请你算一算,完成后林场、牧场的面积各为多少公顷?
根据题意得:
x+y=162
y
20%x
=
解得:
答:林场面积135公顷,牧场面积27公顷。
解:林场面积x公顷,牧场面积y公顷,
经检验,符合题意。
4.某厂第二车间的人数比第一车间的人数的 少30人。如果从第一车间调10人到第二车间,那么第二车间的人数就是第一车间的 。问这两个车间各有多少人?
根据题意得:
y
x-10
y+10
=
解得:
答:第一车间有250人,第二车间有170人。
解:设第一车间有x人,第二车间有y人。
经检验,符合题意。
x
-30
=
( )
5.某般的载重为260吨,容积为1000 m3。现有甲、乙两种货物要运,其中甲种货物每吨体积为8m3,乙种货物每吨体积为2m3,若要充分利用这艘船的载重与容积,甲、乙两种货物应各装多少吨?(设装运货物时无任何空隙)
根据题意得:
x+y=260
8x
+2y
=1000
解得:
答:甲种货物装80吨、乙种货物装180吨。
解:设甲种货物装x吨、乙种货物装y吨。
经检验,符合题意。
6.第一小组的同学分铅笔若干枝。若其中有4人每人各取4枝,其余的人每人取3枝,则还剩16枝;若有1人只取2枝,则其余的人恰好每人各可得6枝,问同学有多少人?铅笔有多少枝?
根据题意得:
16+3(x-4)+16=y
2+6(x-1)=y
解得:
答:同学有8人,铅笔有44枝。
解:同学有x人,铅笔有y枝。
经检验,符合题意。
谢 谢
第7章 一次方程组 复习课件
实际问题
设未知数,列方程组
数学问题
(二元或三元一次方程组)
解方程组
数学问题的解
(二元或三元一次
方程组的解)
检验
实际问题
的答案
一、本章知识结构图
代入法
加减法
(消元)
二、有关概念
1.二元一次方程:通过化简后,只有两个未知数,并且两个未知数的次数都是1,系数都不是0的整式方程,叫做二元一次方程。
2.二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解。
3.二元一次方程组:由两个一次方程组成,共有两个未知数的方程组,叫做二元一次方程组。
4.二元一次方程组的解:使二元一次方程组的两个方程左、右两边的值都相等的两个未知数的值,叫做二元一次方程组的解。
三、方程组的解法
根据方程未知数的系数特征确定用哪一种解法。
基本思想或思路——消元
常用方法——代入法和加减法
用代入法解二元一次方程组的步骤:
1.求表达式:从方程组中选一个系数比较简
单的方程,将此方程中的一个未知数,如y,用
含x的代数式表示;
2.把这个含x的代数式代入另一个方程中,
消去y,得到一个关于x的一元一次方程;
3.解一元一次方程,求出x的值;
4.再把求出的x的值 代入变形后的方程,求
出y的值。
用加减法解二元一次方程组的步骤:
1.利用等式性质把一个或两个方程的两边都
乘以适当的数,变换两个方程的某一个未知数
的系数,使其绝对值相等;
2.把变换系数后的两个方程的两边分别相加或相减,消去一个未知数,得一元一次方程;
3.解这个一元一次方程,求得一个未知数的值 ;
4.把所求的这个未知的值代入方程组中较为简便的一个方程,求出另一个未知数,从而得到方程的解。
解三元一次方程组的基本思路与解二元一次方程组的基本思路一样,即:
三元一次方程组
消元
二元一次方程组
消元
一元一次方程
三元一次方程组的解法
应用题:
列方程组解应用题的一般步骤:
1.审 2.设 3.列 4.解 5.答
一、行程问题:
1.相遇问题:甲的路程+乙的路程=总的路程
(环形跑道):甲的路程+乙的路程=一圈长
2.追及问题:快者的路程-慢者的路程
=原来相距路程
(环形跑道): 快者的路程-慢者的路程=一圈长
3.顺逆问题:顺速=静速+水(风)速
逆速=静速-水(风)速
例1 A、B两地相距36千米。甲从A地出发步行到B地,乙从B地出发步行到A地。两人同时出发,4小时相遇,6小时后,甲所余路程为乙所余路程的2倍,求两人的速度。
解:设甲、乙的速度分别为x千米/小时和y千米/小时。
依题意可得:
解得
答:甲、乙的速度分别为4千米/小时和5千米/小时。
例2 某人要在规定的时间内由甲地赶往乙地,如果他以每小时50千米的速度行驶,就会迟到24分钟,如果他以每小时75千米的速度行驶,就会提前24分钟 到达乙地,求甲、乙两地间的距离。
、
例3 甲、乙二人以不变的速度在环形路上跑步,如果同时同地出发,相向而行,每隔2分钟相遇一次;如果同向而行,每隔6分钟相遇一次。已知甲比乙跑得快,甲、乙每分钟各跑多少圈?
1.某学校现有甲种材料35㎏,乙种材料29㎏,制作A、B两种型号的工艺品,用料情况如下表:
需甲种材料 需乙种材料
1件A型工艺品 0.9㎏ 0.3㎏
1件B型工艺品 0.4㎏ 1㎏
(1)利用这些材料能制作A、B两种工艺品各多少件?
(2)若每公斤甲、乙种材料分别为8元和10元,问制作A、B两种型号的工艺品各需材料多少钱?
二、图表问题
2.某种植大户计划安排10个劳动力来耕作30亩土地,这些土地可以种蔬菜也可以种水稻,种这些作物所需劳动力及预计产值如下表:
每亩所需劳动力(个) 每亩预计产值(元)
蔬菜 3000
水稻 700
(1)为了使所有土地种上作物,全部劳动力都有工作,应安排种蔬菜的劳动力多少人?
(2)这时预计产值是多少?
3. 下表是某一周甲、乙两种股票的收盘价(股票每天交易结束时的价格)
星期一 星期二
甲 12
乙 13.5
张师傅在该周内持有若干甲、乙两种股票,若按照两种股票每天收盘价计算(不计手续费、税费行等),该人账户中星期二比星期一多获利200元,星期三比星期二多获利1300元,试问张师傅持有甲、乙股票各多少股?
12.5
13.3
星期三
星期四
星期五
星期六
12.9
13.9
12.45
13.4
12.75
13.15
休盘
休盘
解:设张师傅持有甲种股票x股,乙种股票y
股,根据题意,得:
解得
答:张师傅持有甲种股票1000股,乙种股票
1500股。
1.入世后,国内各汽车企业展开价格大战,汽车价格大幅下降,有些型号的汽车供不应求。某汽车生产厂接受了一份订单,要在规定的日期内生产一批汽车,如果每天生产35辆,则差10辆完成任务,如果每天生产40辆,则可提前半天完成任务,问订单要多少辆汽车,规定日期是多少天?
三.总量不变问题
四.销售问题:
标价×折扣=售价
售价—进价=利润
利润率=
达标检测
1.22名工人按定额完成了1400件产品,其中三级工每人定额200件,二级工每人定额50件。若这22名工人中只有二级工与三级工,问二级工与三级工各有多少名?
解:设二级工x名,三级工y名。
根据题意得:
x+y=22
50x
+200y
=1400
解得:
经检验,符合题意。
答:二级工20名,三级工2名。
2.有一批机器零件共418个,若甲先做2天,乙再加入合作,则再做2天可超产2个,若乙先做3天,然后两人再共做2天,则还有8个未完成。问甲、乙两人每天各做多少个零件?
根据题意得:
2x
3y
+2(x+y)
=418
解得:
答:甲每天做80个零件,乙每天做50个零件。
解:甲每天做x个零件,乙每天做y个零件。
经检验,符合题意
+2(x+y)
-2
=418
+8
3.为改善富春河的周围环境,县政府决定,将该河上游A地的一部分牧场改为林场。改变后,预计林场和牧场共有162公顷,牧场面积是林场面积的20%。请你算一算,完成后林场、牧场的面积各为多少公顷?
根据题意得:
x+y=162
y
20%x
=
解得:
答:林场面积135公顷,牧场面积27公顷。
解:林场面积x公顷,牧场面积y公顷,
经检验,符合题意。
4.某厂第二车间的人数比第一车间的人数的 少30人。如果从第一车间调10人到第二车间,那么第二车间的人数就是第一车间的 。问这两个车间各有多少人?
根据题意得:
y
x-10
y+10
=
解得:
答:第一车间有250人,第二车间有170人。
解:设第一车间有x人,第二车间有y人。
经检验,符合题意。
x
-30
=
( )
5.某般的载重为260吨,容积为1000 m3。现有甲、乙两种货物要运,其中甲种货物每吨体积为8m3,乙种货物每吨体积为2m3,若要充分利用这艘船的载重与容积,甲、乙两种货物应各装多少吨?(设装运货物时无任何空隙)
根据题意得:
x+y=260
8x
+2y
=1000
解得:
答:甲种货物装80吨、乙种货物装180吨。
解:设甲种货物装x吨、乙种货物装y吨。
经检验,符合题意。
6.第一小组的同学分铅笔若干枝。若其中有4人每人各取4枝,其余的人每人取3枝,则还剩16枝;若有1人只取2枝,则其余的人恰好每人各可得6枝,问同学有多少人?铅笔有多少枝?
根据题意得:
16+3(x-4)+16=y
2+6(x-1)=y
解得:
答:同学有8人,铅笔有44枝。
解:同学有x人,铅笔有y枝。
经检验,符合题意。
谢 谢
