华东师大版七年级下册数学 10.4 中心对称课件 (共20张PPT)
文档属性
| 名称 | 华东师大版七年级下册数学 10.4 中心对称课件 (共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 19:48:03 | ||
图片预览





文档简介
(共20张PPT)
10.4 中心对称
10.4 中心对称教学反思
新课导入
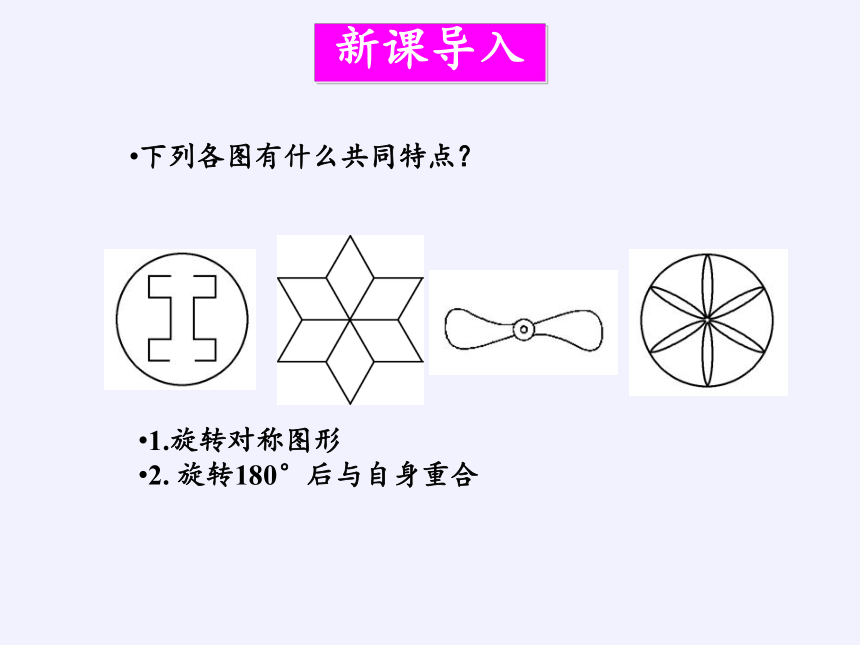
下列各图有什么共同特点?
1.旋转对称图形
2. 旋转180°后与自身重合
【归纳结论】
一个图形绕着旋转中心旋转180°后能与自身重合,我们把这种图形叫做中心对称图形,这个中心叫做对称中心.
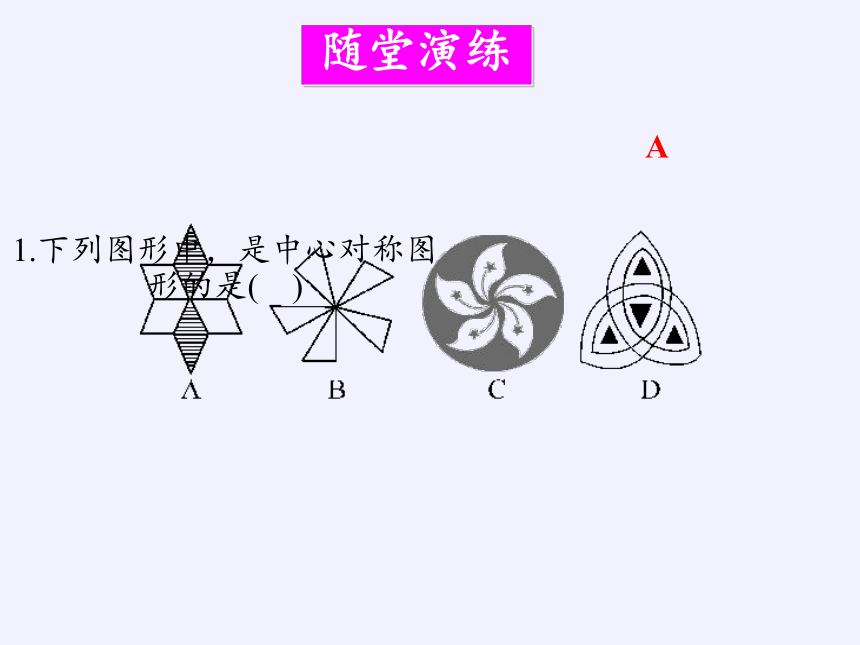
1.下列图形中,是中心对称图形的是( )
随堂演练
A
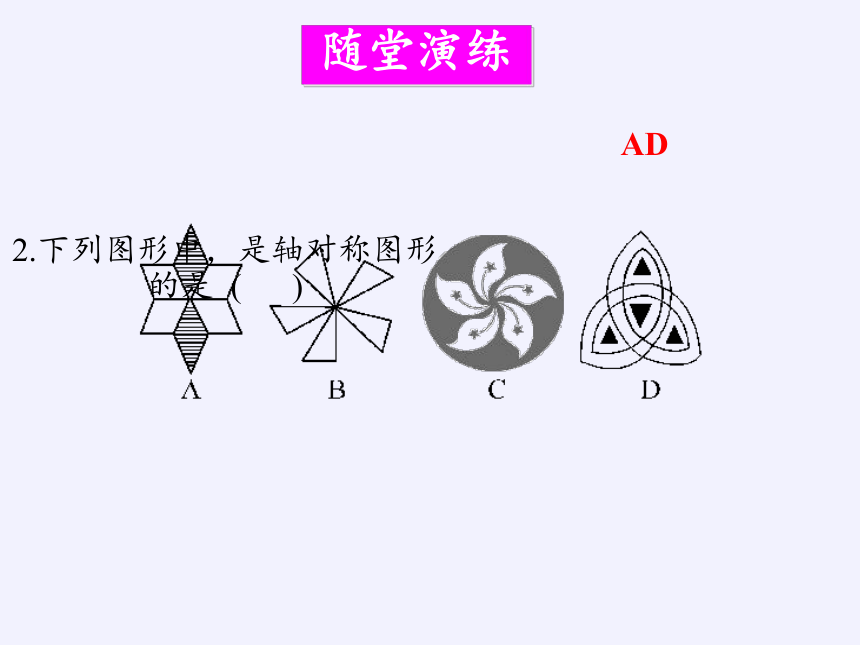
2.下列图形中,是轴对称图形的是 ( )
随堂演练
AD
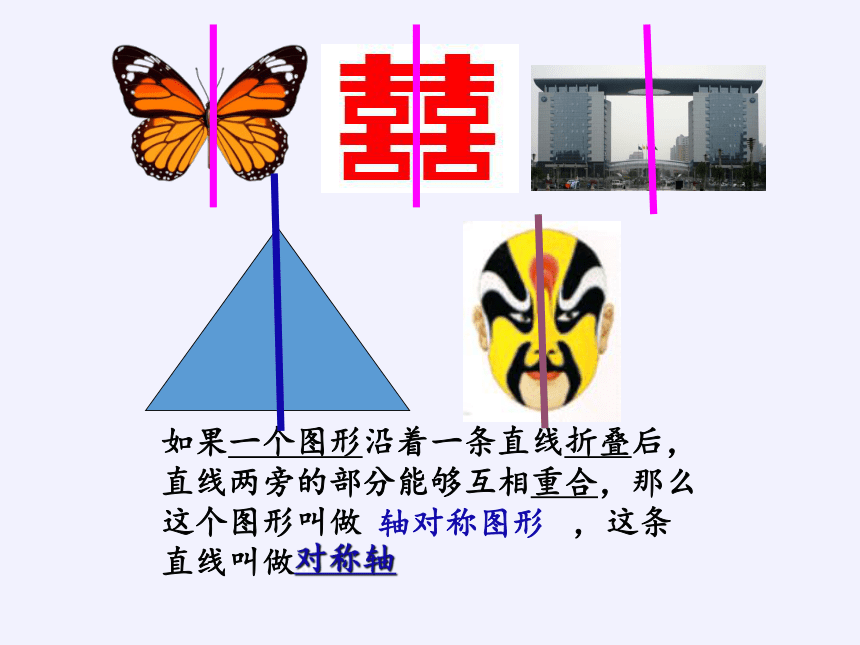
如果一个图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做 ,这条直线叫做。
轴对称图形
对称轴
中心对称与轴对称的联系与区别
3.下列多边形中,是中心对称图形而不是轴对称图形的是( )
A.平行四边形
B.矩形
C.菱形
D.正方形
A
把一个图形沿着某一条直线翻折过去,
如果它能够与另一个图形重合,
那么就说这两个图形成轴对称。
D D1
猜想一下,这两个图形是什么关系呢?
推进新课
【归纳结论】
1.把一个图形绕着某一个点旋180°, 如果它能够和另一个图形重合,
那么就说这两个图形成中心对称。
2.这个点叫做对称中心.
3.这两个图形中的对应点叫做关于中 心的对称点.
4.(P128例)如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.
分析:中心对称就是旋转180°,关于点O成中心对称就是绕点O旋转180°,因此,我们连AO、BO、CO并延长,取与它们相等的线段即可得到.
解:(1)连结AO并延长AO到D,使OD=OA,于是得到点A的对称点D,如图所示.
(2)同样画出点B和点C的对称点E和F.
(3)顺次连结DE、EF、FD.则△DEF即为所求的三角形.
5.按下列要求正确画出图形:
已知四边形ABCD和点O,画出四边形ABCD关于点O成中心对称的四边形.
(2)连接AO并延长至A′,使A′O=AO,连接BO并延长至B′,使B′O=BO,连接CO并延长至C′,使C′O=CO,连接DO并延长至D′,使D′O=DO,然后顺次连接即可.
四边形A′B′C′D′如图所示.
1.中心对称图形
2.轴对称图形与中心对称图形区别
3.成中心对称
4.画中心对称图形
小结
1.教材P131习题第1一2题;
2.完成练习册本课时的习题.
课后作业
读和写是学生最必要的两种学习方法,也是通向周围世界的两扇窗口。——苏霍姆林斯基
谢 谢
10.4 中心对称
10.4 中心对称教学反思
新课导入
下列各图有什么共同特点?
1.旋转对称图形
2. 旋转180°后与自身重合
【归纳结论】
一个图形绕着旋转中心旋转180°后能与自身重合,我们把这种图形叫做中心对称图形,这个中心叫做对称中心.
1.下列图形中,是中心对称图形的是( )
随堂演练
A
2.下列图形中,是轴对称图形的是 ( )
随堂演练
AD
如果一个图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做 ,这条直线叫做。
轴对称图形
对称轴
中心对称与轴对称的联系与区别
3.下列多边形中,是中心对称图形而不是轴对称图形的是( )
A.平行四边形
B.矩形
C.菱形
D.正方形
A
把一个图形沿着某一条直线翻折过去,
如果它能够与另一个图形重合,
那么就说这两个图形成轴对称。
D D1
猜想一下,这两个图形是什么关系呢?
推进新课
【归纳结论】
1.把一个图形绕着某一个点旋180°, 如果它能够和另一个图形重合,
那么就说这两个图形成中心对称。
2.这个点叫做对称中心.
3.这两个图形中的对应点叫做关于中 心的对称点.
4.(P128例)如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.
分析:中心对称就是旋转180°,关于点O成中心对称就是绕点O旋转180°,因此,我们连AO、BO、CO并延长,取与它们相等的线段即可得到.
解:(1)连结AO并延长AO到D,使OD=OA,于是得到点A的对称点D,如图所示.
(2)同样画出点B和点C的对称点E和F.
(3)顺次连结DE、EF、FD.则△DEF即为所求的三角形.
5.按下列要求正确画出图形:
已知四边形ABCD和点O,画出四边形ABCD关于点O成中心对称的四边形.
(2)连接AO并延长至A′,使A′O=AO,连接BO并延长至B′,使B′O=BO,连接CO并延长至C′,使C′O=CO,连接DO并延长至D′,使D′O=DO,然后顺次连接即可.
四边形A′B′C′D′如图所示.
1.中心对称图形
2.轴对称图形与中心对称图形区别
3.成中心对称
4.画中心对称图形
小结
1.教材P131习题第1一2题;
2.完成练习册本课时的习题.
课后作业
读和写是学生最必要的两种学习方法,也是通向周围世界的两扇窗口。——苏霍姆林斯基
谢 谢
