3.1.1方程的根与函数的零点
文档属性
| 名称 | 3.1.1方程的根与函数的零点 |  | |
| 格式 | zip | ||
| 文件大小 | 547.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-05 18:12:44 | ||
图片预览







文档简介
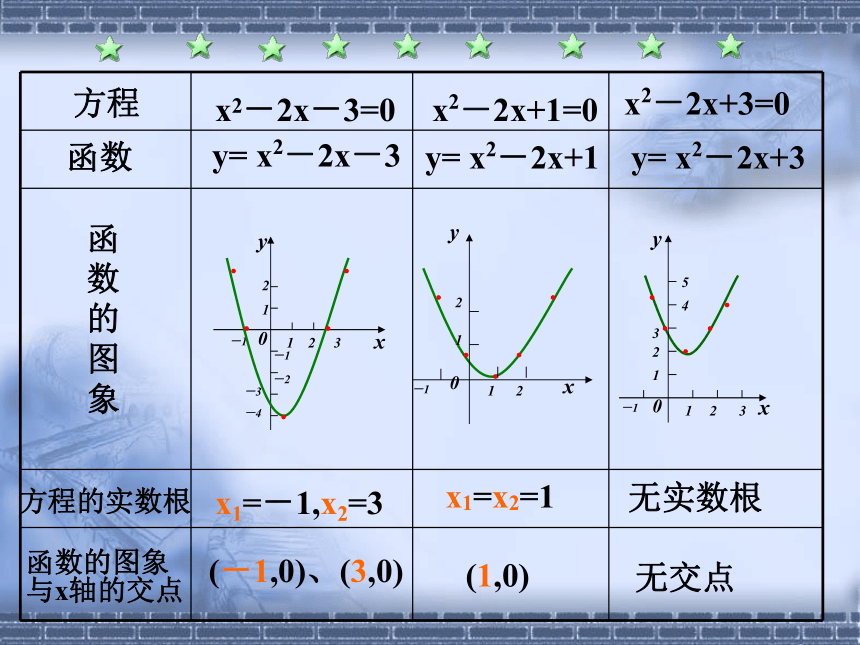
课件27张PPT。 3.1.1方程的根 和 函数的零点方程x2-2x+1=0x2-2x+3=0y= x2-2x-3y= x2-2x+1函数函
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根
函数的图象
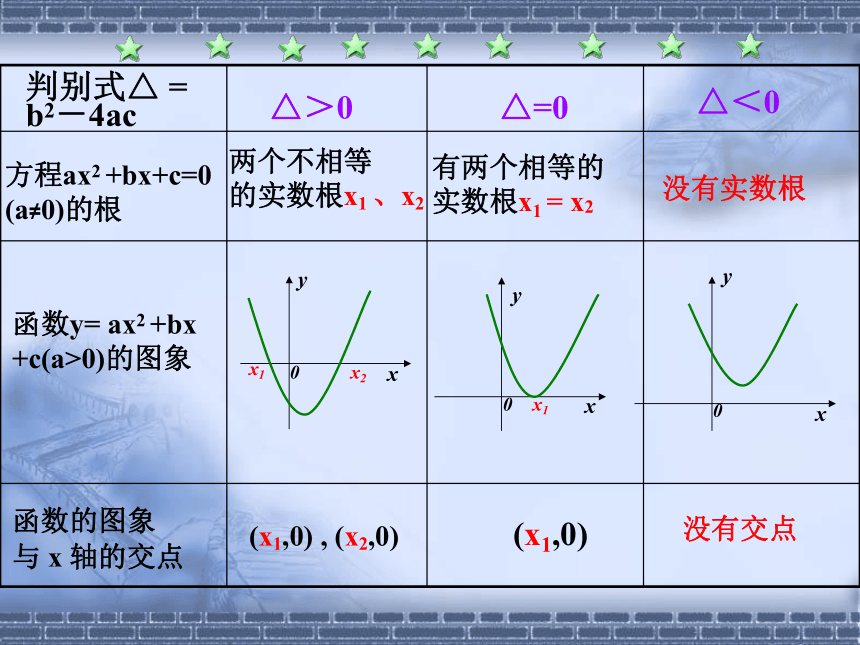
与x轴的交点(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x+3方程ax2 +bx+c=0
(a≠0)的根函数y= ax2 +bx
+c(a>0)的图象判别式△ =
b2-4ac△>0△=0△<0函数的图象
与 x 轴的交点有两个相等的
实数根x1 = x2没有实数根(x1,0) , (x2,0)(x1,0)没有交点两个不相等
的实数根x1 、x2 对于函数y=f(x),我们把使f(x)=0的实数x叫做函数
y=f(x)的零点。一、函数零点的定义:注意:零点指的是一个实数;练习:求下列函数的零点:
(1) ;(2) .求函数零点的方法:
求函数的零点就是求相应的方程的根,一般可以借助求根公式或因式分解等办法,求出方程的根,从而得出函数的零点。方程f(x)=0有实根等价关系例、如果二次函数y=x2+2x+(m+3)有两个不同的零点,则m的取值范围是( )
A m> – 2 B m< – 2 C m>2 D m<2B 探究1:函数f(x)= 2x-1的零点是
什么? 计算f(0)与 f(1)的乘积,有什么特点?函数f(x)=2x-1在零点左侧与右侧函数值的乘积有什么特点? 012345-1-212345-1-2-3-4xy探究2 例2:函数 在下列哪个区间上有零点( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4) C 解法一:练习1:下列函数在区间[1,2]上有零点 的是( )
(A) f(x)=3x2-4x+5 (B) f(x)=x3-5x-5
(C) f(x)=lnx-3x+6 (D) f(x)=ex+3x-6 练习2:f(x)=x3+x-1在下列哪个区间上有
零点( )
A.(-2,-1) B.(0,1) C.(1,2) D.(2,3) D B 练习:由表3-1和图3.1—3可知f(2)<0,f(3)>0,即f(2)·f(3)<0,说明这个函数在区间(2,3)内
有零点。 由于函数f(x)在定义域
(0,+∞)内是增函数,所以
它仅有一个零点。解:用计算器或计算机作出x、f(x)的对应值表-4 -1.30691.09863.38635.60947.79189.945912.079414.1972例3、求函数f(x)=lnx+2x-6的零点个数。三、判断零点的方法:(1)定义法:解方程 f(x)=0,
得出函数的零点。(2)图象法:画出y= f(x)的图象,其图象与x轴交点的横坐标。(3)定理法:函数零点存在性定理。C 解法二: 例4:函数 在下列哪个
区间上有零点( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4) 函数f(x)=g(x)-h(x)的零点 课堂小结: 1、函数零点的定义;2、函数的零点与方程的根的关系;3、确定函数的零点的方法。 课后作业:
1、求下列函数的零点:(1)y=-x2+6x+7;
(2)y=x3-4x。
2、若函数f(x)=x2-ax-b的两个零点是2和3,
求loga25 + b2。
3、练习册 P50 例2,例3 P84 2,5
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根
函数的图象
与x轴的交点(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x+3方程ax2 +bx+c=0
(a≠0)的根函数y= ax2 +bx
+c(a>0)的图象判别式△ =
b2-4ac△>0△=0△<0函数的图象
与 x 轴的交点有两个相等的
实数根x1 = x2没有实数根(x1,0) , (x2,0)(x1,0)没有交点两个不相等
的实数根x1 、x2 对于函数y=f(x),我们把使f(x)=0的实数x叫做函数
y=f(x)的零点。一、函数零点的定义:注意:零点指的是一个实数;练习:求下列函数的零点:
(1) ;(2) .求函数零点的方法:
求函数的零点就是求相应的方程的根,一般可以借助求根公式或因式分解等办法,求出方程的根,从而得出函数的零点。方程f(x)=0有实根等价关系例、如果二次函数y=x2+2x+(m+3)有两个不同的零点,则m的取值范围是( )
A m> – 2 B m< – 2 C m>2 D m<2B 探究1:函数f(x)= 2x-1的零点是
什么? 计算f(0)与 f(1)的乘积,有什么特点?函数f(x)=2x-1在零点左侧与右侧函数值的乘积有什么特点? 012345-1-212345-1-2-3-4xy探究2 例2:函数 在下列哪个区间上有零点( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4) C 解法一:练习1:下列函数在区间[1,2]上有零点 的是( )
(A) f(x)=3x2-4x+5 (B) f(x)=x3-5x-5
(C) f(x)=lnx-3x+6 (D) f(x)=ex+3x-6 练习2:f(x)=x3+x-1在下列哪个区间上有
零点( )
A.(-2,-1) B.(0,1) C.(1,2) D.(2,3) D B 练习:由表3-1和图3.1—3可知f(2)<0,f(3)>0,即f(2)·f(3)<0,说明这个函数在区间(2,3)内
有零点。 由于函数f(x)在定义域
(0,+∞)内是增函数,所以
它仅有一个零点。解:用计算器或计算机作出x、f(x)的对应值表-4 -1.30691.09863.38635.60947.79189.945912.079414.1972例3、求函数f(x)=lnx+2x-6的零点个数。三、判断零点的方法:(1)定义法:解方程 f(x)=0,
得出函数的零点。(2)图象法:画出y= f(x)的图象,其图象与x轴交点的横坐标。(3)定理法:函数零点存在性定理。C 解法二: 例4:函数 在下列哪个
区间上有零点( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4) 函数f(x)=g(x)-h(x)的零点 课堂小结: 1、函数零点的定义;2、函数的零点与方程的根的关系;3、确定函数的零点的方法。 课后作业:
1、求下列函数的零点:(1)y=-x2+6x+7;
(2)y=x3-4x。
2、若函数f(x)=x2-ax-b的两个零点是2和3,
求loga25 + b2。
3、练习册 P50 例2,例3 P84 2,5
