幂函数
图片预览









文档简介
课件30张PPT。2.3幂
函
数问题1:如果张红购买了每千克1元的蔬菜x千克,那
么她需要付的钱数y(元)和购买的蔬菜量x
(千克)之间有何关系?
问题2:如果正方形的边长为x,那么正方形面积y=?
问题3:如果正方体的棱长为x,那么正方体体积y= ?
问题4:如果正方形场地的面积为x,那么正方形的边长
y= ?
问题5:如果某人x秒内骑车行进1千米,那么他骑车的
平均速度y= ?(千米/秒)问题情境
你能发现这几个函数解析式有什么共同点吗?
探索发现注意:幂函数中α可以为任意实数.一、定义一般地,函数 叫做幂函数(power fun_ction) ,
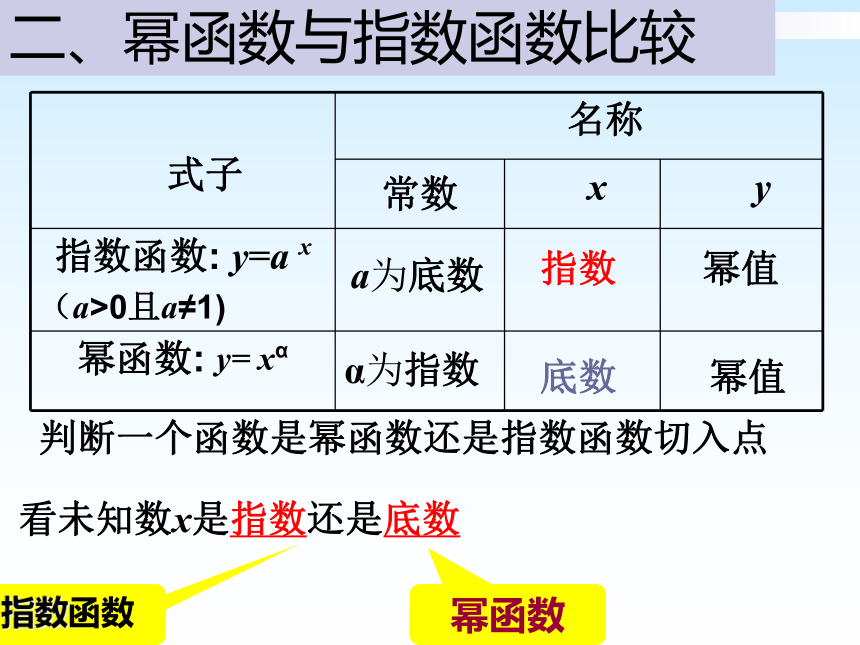
其中x为自变量, 为常数。a为底数指数α为指数底数幂值幂值二、幂函数与指数函数比较判断一个函数是幂函数还是指数函数切入点看未知数x是指数还是底数幂函数指数函数问题:
幂函数的解析式有什么特点?
(1)都是以自变量x为底数;
(2)指数为常数;
(3)自变量x前的系数为1;练习1、下列函数中,哪几个函数是幂函数?
(1)y = (2)y=2x2
(3)y=2x (4)y=1
(5) y=x2 +2 (6) y=-x3答案:(1) 三、幂函数的图象与性质试作出下列函数的图象
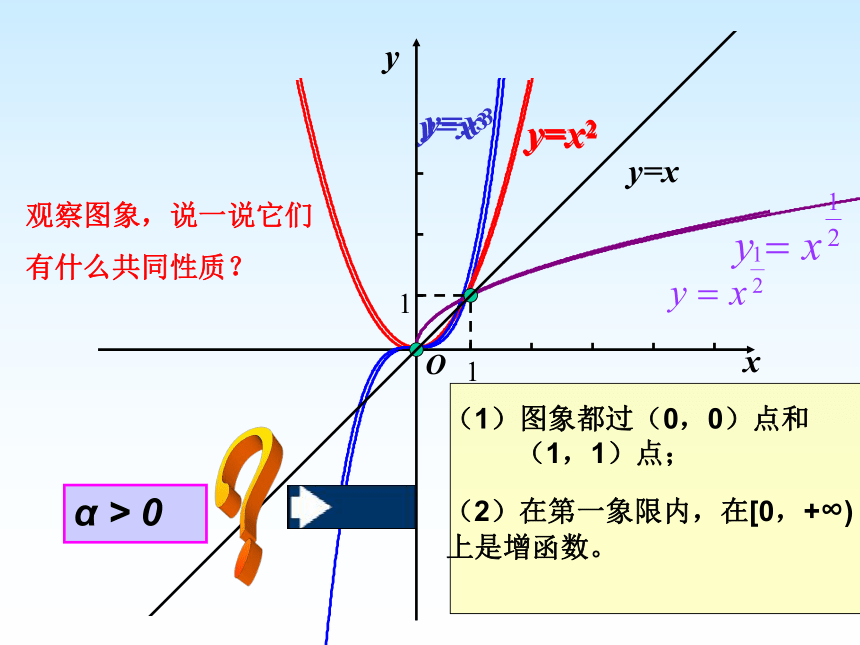
xOy=x2yy=x311y=x(1)图象都过(0,0)点和
(1,1)点;
(2)在第一象限内,在[0,+∞)上是增函数。 α > 0观察图象,说一说它们
有什么共同性质??试作出下列函数的图象
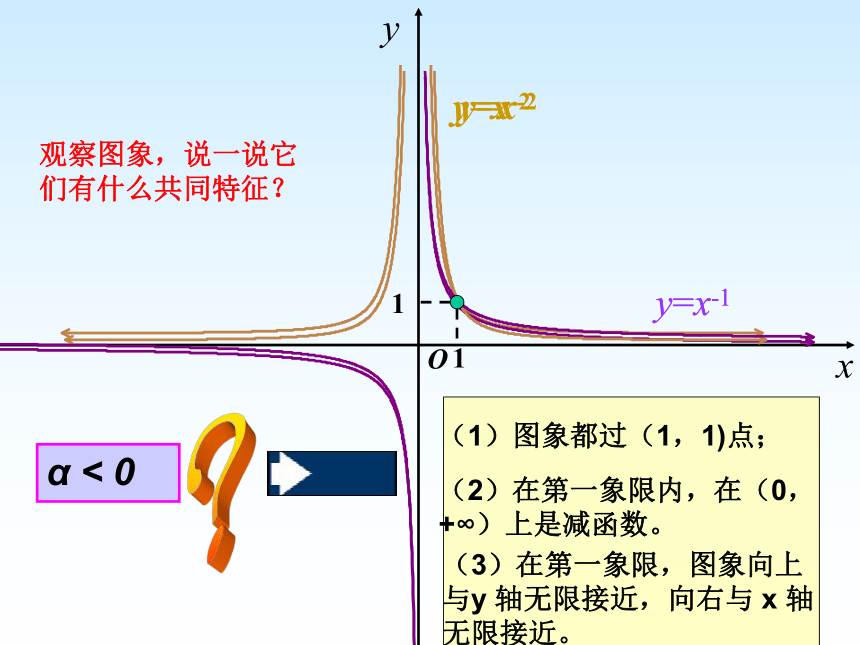
y=x-2y=x-111观察图象,说一说它们有什么共同特征?(1)图象都过(1,1)点;(2)在第一象限内,在(0,+∞)上是减函数。
(3)在第一象限,图象向上
与y 轴无限接近,向右与 x 轴无限接近。α < 0?奇偶
奇非奇
非偶奇(1,1)RRR{x|x≠0}[0,+∞)RR{y|y≠0}[0,+∞)[0,+∞)在R上增在(-∞,0)上减,观察幂函数图象,将你发现的结论写在下表:在R上增在[0,+∞)上增,在(-∞,0]上减,在[0,+∞)上增,在(0,+∞)上减XyXy第一象限k<0时k>0时双曲线型0<k<1开口 向右型抛物线OOk<0画出函数在第一象限的图象后,再根据函数的奇偶性,画出函数在其他象限还有的图象K=0,直线型k>1开口向上型抛物线K=1图象过一不过四(都过第一象限,
不过第四象限)y(A)(B)(I)(C)X(G)(H)(D)(J)(F)IGEBCAHJDF练习2XXXXXXXXXOOOOOOOOOOyyyyyyyy(E)y例2
如果函数 是幂函数,且在区间(0,+∞)内是减函数,求满足条件的实数m的集合。解:依题意,得解方程,得 m=2或m=-1当 m=2时,函数为不合题意,舍去.当m=-1时,函数为符合题意.所以m=2
变式:幂函数 的图象与
坐标轴无交点,且关于y轴对称,
求m的值。
解:(1)y= x0.8在(0,+∞)内是增函数,
∵5.2<5.3 ∴ 5.20.8 < 5.30.8 (2)y=x0.3在(0,+∞)内是增函数
∵0.2<0.3∴ 0.20.3 <0.30.3(3)y=x-2/5在(0,+∞)内是减函数
∵2.5<2.7∴ 2.5-2/5>2.7-2/5比较大小:>解后反思
两个数比较大小时,何时用幂函数模型,何时用指数函数模型? 练习3<<>≤ 如图所示,曲线是幂函数
在第一象限内的图象,
已知 分别取 四个值,则相应图象依次为:
______________规律:在第一象限作直线 ,它同各幂函
数图象相交,按交点从下到上的顺序,幂指数
按从小到大的顺序排列 c4c3c2c1oyx2211例5、归纳:幂函数图象在第一象限的分布情况例6 试写出函数 的定义域,并指出其奇偶性、值域. 练习:求幂函数 的定义域、奇偶性 和值域。 它的定义域是(0,+∞)解: (1)奇偶性:∵定义域不关于原点对称, ∴为非奇非偶函数.证明幂函数 在[0,+∞)上是增函数.复习用定义证明函数的单调性的步骤:(1). 设x1, x2是某个区间上任意二值,且x1<x2;(2). 作差 f(x1)-f(x2),变形 ;(3). 判断 f(x1)-f(x2) 的符号;(4). 下结论.例7证明:任取所以幂函数 在[0,+∞)上是增函数. 证法二: 任取x1 ,x2 ∈[0,+∞),且x1< x2 ; 证明幂函数 在[0,+∞)上是增函数.(1)作差法:若给出的函数是有根号的式子,往往采用有理化的方式。
(2)作商法:证明时要注意分子和分母均为正数,否则不一定能推出f(x1)<f(x2)。即所以幂函数定义五个特殊幂函数图象基本性质本节知识结构:作业:
1、书本79页1,2,3
2、如果函数 是幂函数,并且是奇函数,求满足条件的实数m的值。
3、利用单调性判断下列各值的大小。
再见
函
数问题1:如果张红购买了每千克1元的蔬菜x千克,那
么她需要付的钱数y(元)和购买的蔬菜量x
(千克)之间有何关系?
问题2:如果正方形的边长为x,那么正方形面积y=?
问题3:如果正方体的棱长为x,那么正方体体积y= ?
问题4:如果正方形场地的面积为x,那么正方形的边长
y= ?
问题5:如果某人x秒内骑车行进1千米,那么他骑车的
平均速度y= ?(千米/秒)问题情境
你能发现这几个函数解析式有什么共同点吗?
探索发现注意:幂函数中α可以为任意实数.一、定义一般地,函数 叫做幂函数(power fun_ction) ,
其中x为自变量, 为常数。a为底数指数α为指数底数幂值幂值二、幂函数与指数函数比较判断一个函数是幂函数还是指数函数切入点看未知数x是指数还是底数幂函数指数函数问题:
幂函数的解析式有什么特点?
(1)都是以自变量x为底数;
(2)指数为常数;
(3)自变量x前的系数为1;练习1、下列函数中,哪几个函数是幂函数?
(1)y = (2)y=2x2
(3)y=2x (4)y=1
(5) y=x2 +2 (6) y=-x3答案:(1) 三、幂函数的图象与性质试作出下列函数的图象
xOy=x2yy=x311y=x(1)图象都过(0,0)点和
(1,1)点;
(2)在第一象限内,在[0,+∞)上是增函数。 α > 0观察图象,说一说它们
有什么共同性质??试作出下列函数的图象
y=x-2y=x-111观察图象,说一说它们有什么共同特征?(1)图象都过(1,1)点;(2)在第一象限内,在(0,+∞)上是减函数。
(3)在第一象限,图象向上
与y 轴无限接近,向右与 x 轴无限接近。α < 0?奇偶
奇非奇
非偶奇(1,1)RRR{x|x≠0}[0,+∞)RR{y|y≠0}[0,+∞)[0,+∞)在R上增在(-∞,0)上减,观察幂函数图象,将你发现的结论写在下表:在R上增在[0,+∞)上增,在(-∞,0]上减,在[0,+∞)上增,在(0,+∞)上减XyXy第一象限k<0时k>0时双曲线型0<k<1开口 向右型抛物线OOk<0画出函数在第一象限的图象后,再根据函数的奇偶性,画出函数在其他象限还有的图象K=0,直线型k>1开口向上型抛物线K=1图象过一不过四(都过第一象限,
不过第四象限)y(A)(B)(I)(C)X(G)(H)(D)(J)(F)IGEBCAHJDF练习2XXXXXXXXXOOOOOOOOOOyyyyyyyy(E)y例2
如果函数 是幂函数,且在区间(0,+∞)内是减函数,求满足条件的实数m的集合。解:依题意,得解方程,得 m=2或m=-1当 m=2时,函数为不合题意,舍去.当m=-1时,函数为符合题意.所以m=2
变式:幂函数 的图象与
坐标轴无交点,且关于y轴对称,
求m的值。
解:(1)y= x0.8在(0,+∞)内是增函数,
∵5.2<5.3 ∴ 5.20.8 < 5.30.8 (2)y=x0.3在(0,+∞)内是增函数
∵0.2<0.3∴ 0.20.3 <0.30.3(3)y=x-2/5在(0,+∞)内是减函数
∵2.5<2.7∴ 2.5-2/5>2.7-2/5比较大小:>解后反思
两个数比较大小时,何时用幂函数模型,何时用指数函数模型? 练习3<<>≤ 如图所示,曲线是幂函数
在第一象限内的图象,
已知 分别取 四个值,则相应图象依次为:
______________规律:在第一象限作直线 ,它同各幂函
数图象相交,按交点从下到上的顺序,幂指数
按从小到大的顺序排列 c4c3c2c1oyx2211例5、归纳:幂函数图象在第一象限的分布情况例6 试写出函数 的定义域,并指出其奇偶性、值域. 练习:求幂函数 的定义域、奇偶性 和值域。 它的定义域是(0,+∞)解: (1)奇偶性:∵定义域不关于原点对称, ∴为非奇非偶函数.证明幂函数 在[0,+∞)上是增函数.复习用定义证明函数的单调性的步骤:(1). 设x1, x2是某个区间上任意二值,且x1<x2;(2). 作差 f(x1)-f(x2),变形 ;(3). 判断 f(x1)-f(x2) 的符号;(4). 下结论.例7证明:任取所以幂函数 在[0,+∞)上是增函数. 证法二: 任取x1 ,x2 ∈[0,+∞),且x1< x2 ; 证明幂函数 在[0,+∞)上是增函数.(1)作差法:若给出的函数是有根号的式子,往往采用有理化的方式。
(2)作商法:证明时要注意分子和分母均为正数,否则不一定能推出f(x1)<f(x2)。即所以幂函数定义五个特殊幂函数图象基本性质本节知识结构:作业:
1、书本79页1,2,3
2、如果函数 是幂函数,并且是奇函数,求满足条件的实数m的值。
3、利用单调性判断下列各值的大小。
再见
