2.2.2对数函数及其性质(三课时)
文档属性
| 名称 | 2.2.2对数函数及其性质(三课时) |  | |
| 格式 | zip | ||
| 文件大小 | 342.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-05 18:15:35 | ||
图片预览










文档简介
课件34张PPT。§2.2.2 对数函数及其性质一、引入课题 某种细胞1个分裂成2个,2个分裂成4个,4个分裂成8个……则1个这 样的细胞分裂x次后得到细胞个数y是分裂次数x的函数,关系式为:y = 2 x 反过来,研究分裂多少次可以得到1万个细胞,10万个……则此时分裂次数 x 与细胞的个数 y 的关系式是什么?x是y的函数吗?根据对数的定义得到的函数为:x = log 2 y习惯上表示为: y = log 2 x1 、对数函数的概念:
二 新课其中x是自变量,定义域是 .思考:
1、指数函数概念中a的取值范围是什么?你能说出对数函数的概念中a的取值范围吗?2、指数函数定义域、值域是什么?那么,你能求出对数函数的吗?3、指数函数的解析式有什么特征?那么,对数函数呢?练习:判断下列函数是否是对数函数?结论:看对数符号前面系数是否是1,看底数是否是符合条件的常数,看真数的位置上是否只有一个x.列表描点连线 我们在学习指数函数的时候,根据
什么思路来研究指数函数的性质?对
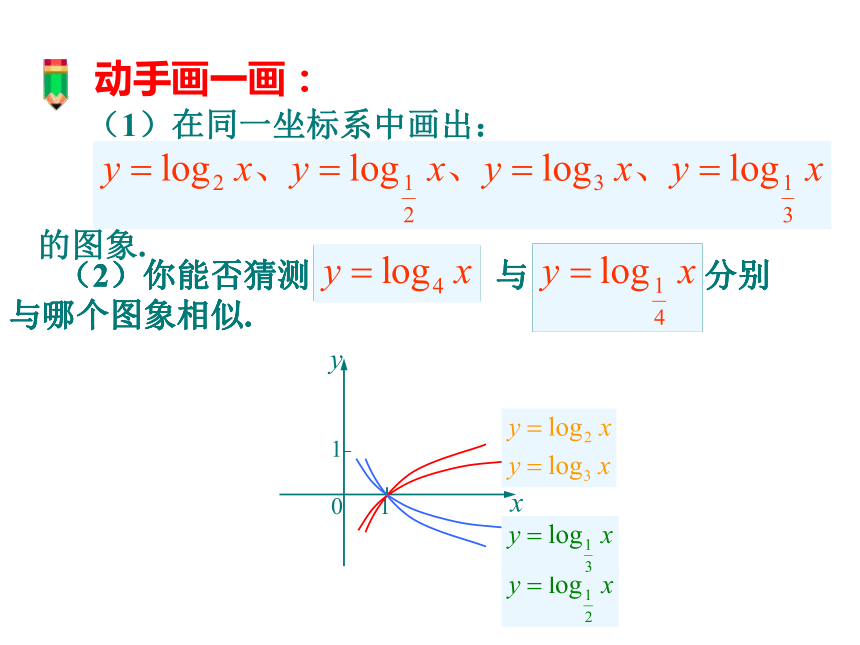
数函数呢?回顾0 11 (1)在同一坐标系中画出:
的图象. (2)你能否猜测 与 分别与哪个图象相似.xy动手画一画: (2)你能否猜测 与 分别与哪个图象相似.猜想:
是不是所有底数互为倒数的对数函数的图象都关于x轴对称呢? 结论:
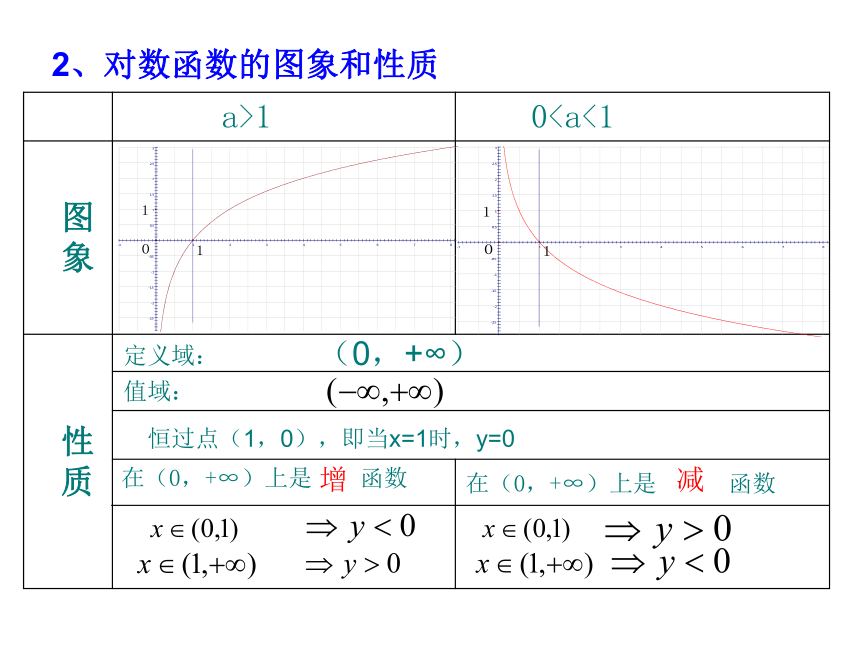
底数互为倒数的两个对数函数的图象关于x轴对称。探究在(0,+∞)上是 函数在(0,+∞)上是 函数
值域:定义域:性
质
图
象 012、对数函数的图象和性质
(0,+∞)恒过点(1,0),即当x=1时,y=0 增减深入探究图象与底数的关系:在第一象限按顺时针方向底数增大练习册P42 例1,变式1—1 在第一象限按顺时针方向底数增大。 补充性质二 底数互为倒数的两个对数函数的图象关于x轴对称。补充性质一
图
形10xy先看y=2x 与y=log2x指数函数、对数函数的图象有何关系呢?y=2xy=xy=log2xy=2x指数函数与对数函数图象间的关系指数函数与对数函数图象间的关系3、指数函数与对数函数的图象的关系:函数 y=f(x) 的反函数记作:y=f-1(x) 4、反函数(1)函数与其反函数的图象关于直线 y= x 对称。(2)函数的定义域是其反函数的值域,值域是
其反函数的定义域。5、对数函数的图象和性质的应用例1、比较下列各数的大小. (1) log23.4 , log28.5 ;(2) log0.31.8 , log0.32.7; (3) loga5.1, loga5.9 (a>0,a≠1)
(4)log 67 , log 7 6 ;
(5)log 32, log 2 0.8 .类型1:利用单调性比较大小小 结比较大小的方法(1) 利用函数单调性(同底数)(2) 利用中间值(如: 0,1.)(3) 利用图象比较(在第一象限按顺时针方向底数增大)例2 解下列关于x的不等式:(1) log0.5x > log0.5(1-x)(2) log2(x+3) > 2 依据:单调性(3)类型2:利用单调性解不等式例3 求下列函数的定义域.类型3:求函数的定义域小 结求函数定义域的方法:1. 分数的分母不能为零;3. 偶次方根的被开方数大于等于零;4. 对数的真数必须大于零;5. 指数、对数的底数必须大于零且不等于1.2. 零的指数不能为零和负数;变式:
例4:求函数 y=log3x(1≤x≤3)的值域.(1)已知函数y=logax(a>0,a≠1),当x∈[3,9]时,函数的最大值比最小值大1,
则a=________(2)求函数 y=log3(x2-4x+7)的值域.类型4:求函数的值域类型5:求复合函数的单调区间小结 :1.对数函数的定义:函数 叫做对数函数; 它是指数函数 的反函数。的定义域为 值域为 小结 :2.对数函数的图象和性质
(0,+∞)过点(1,0),即当x=1时,y=0 增减 在第一象限按顺时针方向底数增大。 补充性质二 底数互为倒数的两个对数函数的图象关于x轴对称。补充性质一
图
形10xy函数 y=f(x) 的反函数记作:y=f-1(x) 函数与其反函数的图象关于直线 y= x 对称。3、指数函数与对数函数的图像的关系:作业:P73练习3 P74习题8
练习册P80 2, 6P73 练习2 P 74习题7
补充:1、求函数
的值域。
二 新课其中x是自变量,定义域是 .思考:
1、指数函数概念中a的取值范围是什么?你能说出对数函数的概念中a的取值范围吗?2、指数函数定义域、值域是什么?那么,你能求出对数函数的吗?3、指数函数的解析式有什么特征?那么,对数函数呢?练习:判断下列函数是否是对数函数?结论:看对数符号前面系数是否是1,看底数是否是符合条件的常数,看真数的位置上是否只有一个x.列表描点连线 我们在学习指数函数的时候,根据
什么思路来研究指数函数的性质?对
数函数呢?回顾0 11 (1)在同一坐标系中画出:
的图象. (2)你能否猜测 与 分别与哪个图象相似.xy动手画一画: (2)你能否猜测 与 分别与哪个图象相似.猜想:
是不是所有底数互为倒数的对数函数的图象都关于x轴对称呢? 结论:
底数互为倒数的两个对数函数的图象关于x轴对称。探究在(0,+∞)上是 函数在(0,+∞)上是 函数
值域:定义域:性
质
图
象 0
(0,+∞)恒过点(1,0),即当x=1时,y=0 增减深入探究图象与底数的关系:在第一象限按顺时针方向底数增大练习册P42 例1,变式1—1 在第一象限按顺时针方向底数增大。 补充性质二 底数互为倒数的两个对数函数的图象关于x轴对称。补充性质一
图
形10xy先看y=2x 与y=log2x指数函数、对数函数的图象有何关系呢?y=2xy=xy=log2xy=2x指数函数与对数函数图象间的关系指数函数与对数函数图象间的关系3、指数函数与对数函数的图象的关系:函数 y=f(x) 的反函数记作:y=f-1(x) 4、反函数(1)函数与其反函数的图象关于直线 y= x 对称。(2)函数的定义域是其反函数的值域,值域是
其反函数的定义域。5、对数函数的图象和性质的应用例1、比较下列各数的大小. (1) log23.4 , log28.5 ;(2) log0.31.8 , log0.32.7; (3) loga5.1, loga5.9 (a>0,a≠1)
(4)log 67 , log 7 6 ;
(5)log 32, log 2 0.8 .类型1:利用单调性比较大小小 结比较大小的方法(1) 利用函数单调性(同底数)(2) 利用中间值(如: 0,1.)(3) 利用图象比较(在第一象限按顺时针方向底数增大)例2 解下列关于x的不等式:(1) log0.5x > log0.5(1-x)(2) log2(x+3) > 2 依据:单调性(3)类型2:利用单调性解不等式例3 求下列函数的定义域.类型3:求函数的定义域小 结求函数定义域的方法:1. 分数的分母不能为零;3. 偶次方根的被开方数大于等于零;4. 对数的真数必须大于零;5. 指数、对数的底数必须大于零且不等于1.2. 零的指数不能为零和负数;变式:
例4:求函数 y=log3x(1≤x≤3)的值域.(1)已知函数y=logax(a>0,a≠1),当x∈[3,9]时,函数的最大值比最小值大1,
则a=________(2)求函数 y=log3(x2-4x+7)的值域.类型4:求函数的值域类型5:求复合函数的单调区间小结 :1.对数函数的定义:函数 叫做对数函数; 它是指数函数 的反函数。的定义域为 值域为 小结 :2.对数函数的图象和性质
(0,+∞)过点(1,0),即当x=1时,y=0 增减 在第一象限按顺时针方向底数增大。 补充性质二 底数互为倒数的两个对数函数的图象关于x轴对称。补充性质一
图
形10xy函数 y=f(x) 的反函数记作:y=f-1(x) 函数与其反函数的图象关于直线 y= x 对称。3、指数函数与对数函数的图像的关系:作业:P73练习3 P74习题8
练习册P80 2, 6P73 练习2 P 74习题7
补充:1、求函数
的值域。
