抛物线的简单几何性质
图片预览

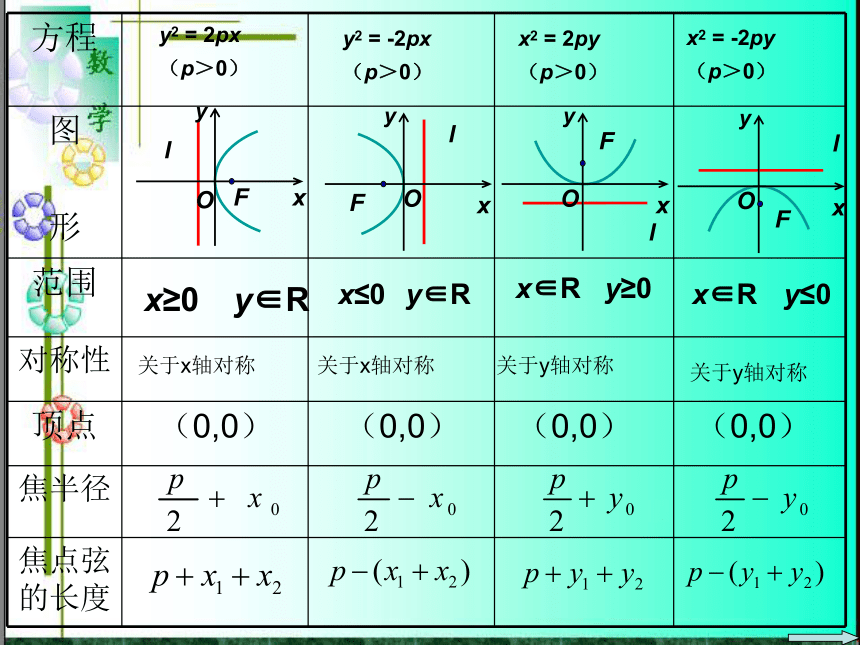


文档简介
课件27张PPT。抛物线的简单几何性质(2)y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
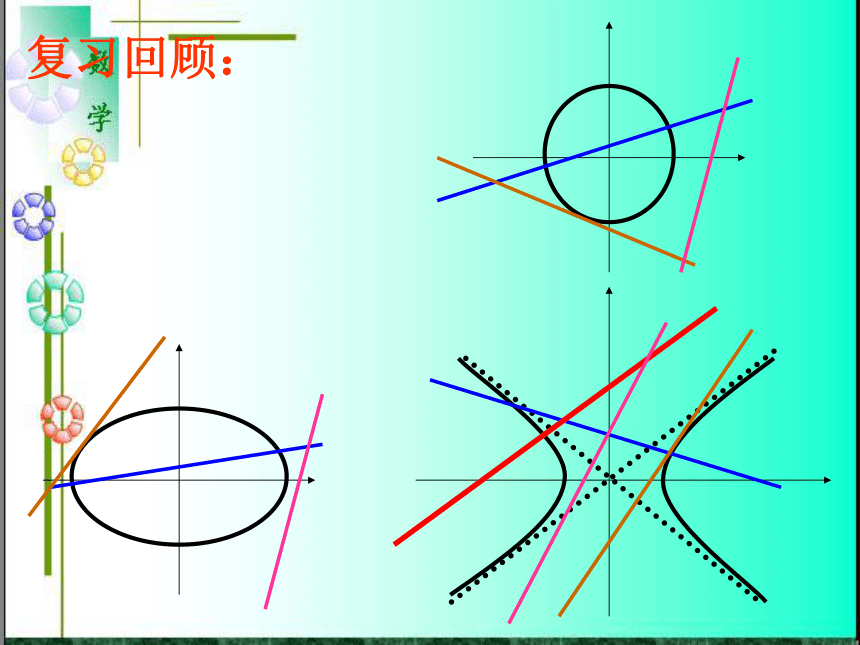
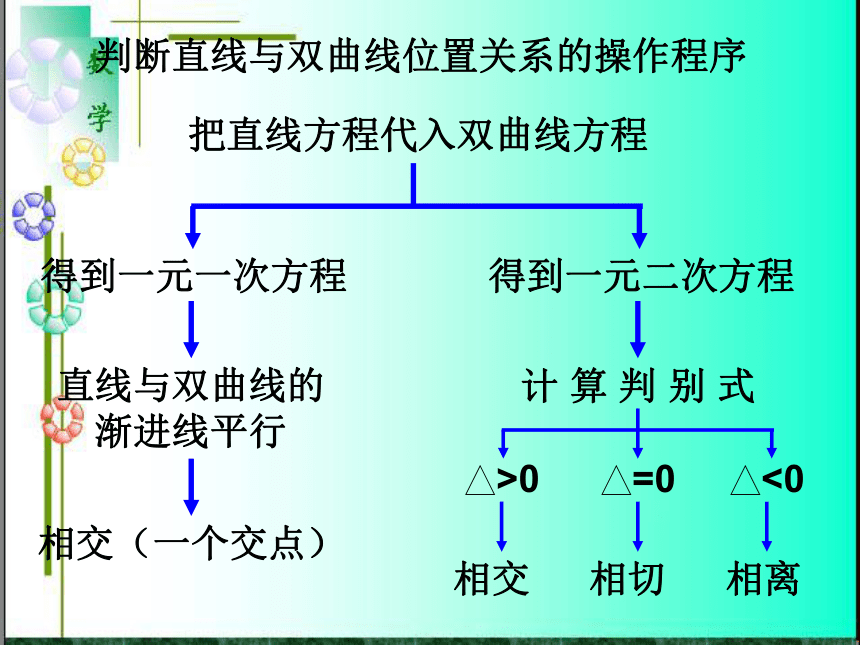
(p>0)关于x轴对称 关于x轴对称 关于y轴对称 关于y轴对称(0,0)(0,0)(0,0)(0,0)复习回顾:直线与圆、椭圆、双曲线的位置关系的判断方法:1、根据几何图形判断的直接判断2、直线与圆锥曲线的公共点的个数 形判断直线与双曲线位置关系的操作程序把直线方程代入双曲线方程得到一元一次方程得到一元二次方程直线与双曲线的
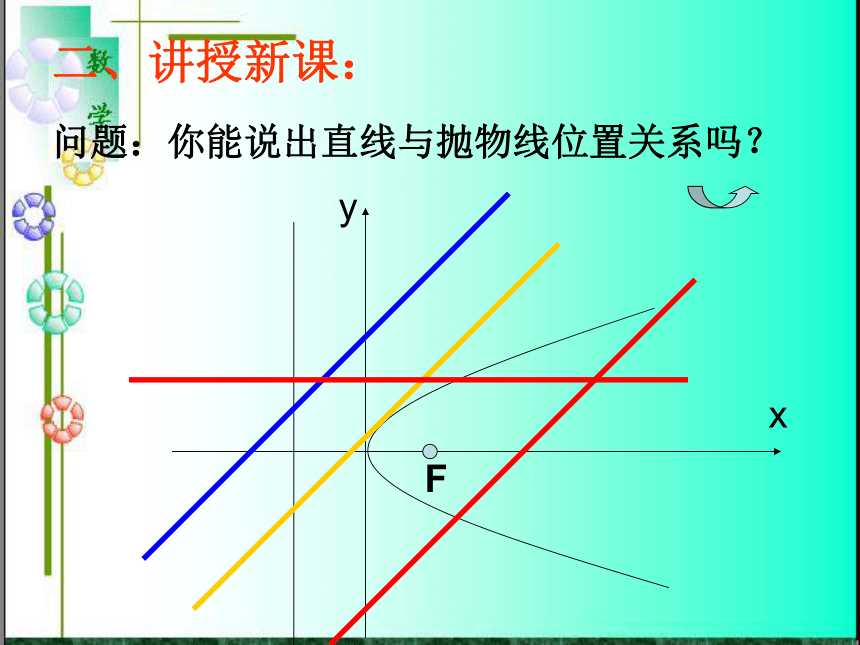
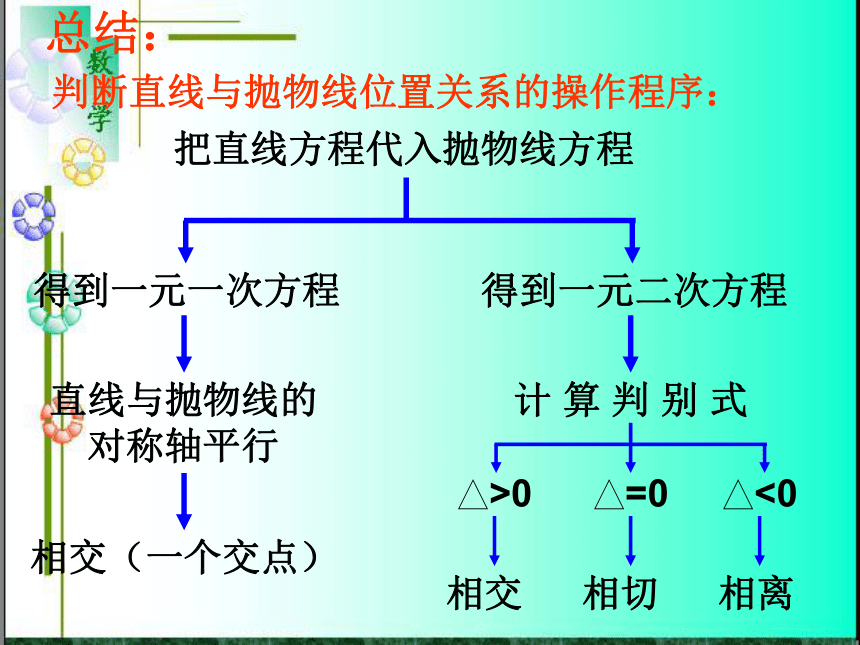
渐进线平行相交(一个交点) 计 算 判 别 式Fxy问题:你能说出直线与抛物线位置关系吗?二、讲授新课:判断直线与抛物线位置关系的操作程序:把直线方程代入抛物线方程得到一元一次方程得到一元二次方程直线与抛物线的
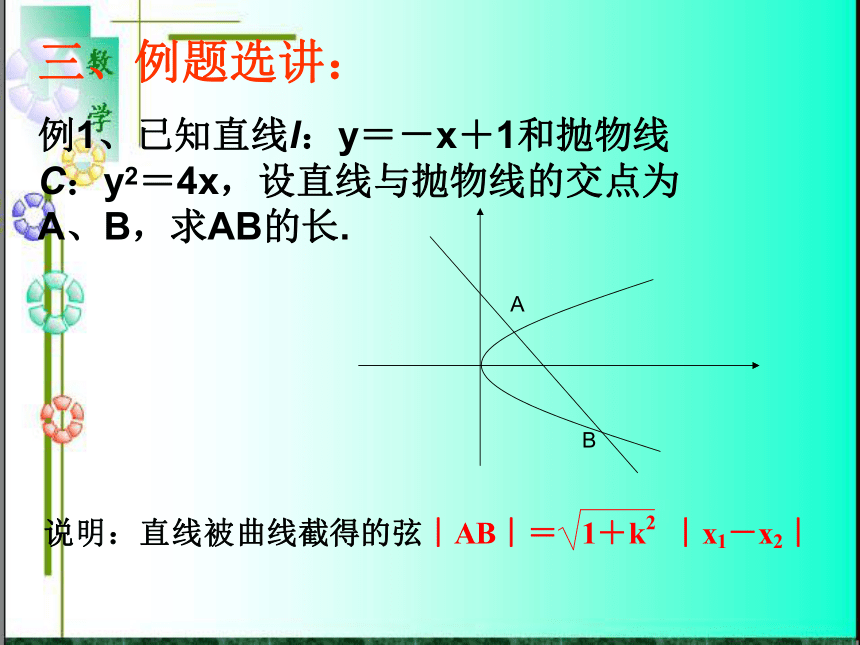
对称轴平行相交(一个交点) 计 算 判 别 式总结:例1、已知直线l:y=-x+1和抛物线
C:y2=4x,设直线与抛物线的交点为
A、B,求AB的长. 三、例题选讲:例2、已知抛物线C:y2=4x,设直线与抛物线两交点为A、B,且线段AB中点为M(2,1),求直线l的方程.说明:中点弦问题的解决方法:
①联立直线方程与曲线方程求解
②点差法1、求过定点(0,2),且与抛物线y2=4x相切的直线方程. 说明:(1)联立方程组,结合判别式求解
(2)注意斜率不存在的情形练习:1、在抛物线y2=64x上求一点,使它到直线L:4x+3y+46=0的距离最短,并求此距离.2、已知抛物线y=x2,动弦AB的长为2,求AB中点纵坐标的最小值.FABM解:解法二:FABM2、已知抛物线y=x2,动弦AB的长为2,求AB中点纵坐标的最小值.3、已知抛物线y2=2x,过Q(2,1)作直线与抛物线交于A、B,求AB中点的轨迹方程.解:焦点F(0,1/4a),准线y=-1/4a,设P(x1,y1),Q(x2,y2),
直线PQ:x=ky+k/4a 由抛物线第二定义, p=PF=y1+1/4a, q=PF2=y2+1/4a 联立y=ax^2,x=ky+k/4a, 得16a^2k^2y^2+(8ak^2-16a)y+k^2=0 ∴y1+y2=(16a-8ak^2)/16a^2k^2=(2-k^2)/2ak^2, y1y2=k^2/16a^2k^2=1/16a^2 1/p+1/q=1/(y1+1/4a)+1/(y2+1/4a)=[(y1+y2)+1/2a]/[y1y2+(y1+y2)/4a+1/16a^2] =[(2-k^2)/2ak^2+1/2a]/[1/16a^2+(2-k^2)/2ak^2/4a+1/16a^2](同乘8a^2k^2) =[4a(2-k^2)+4ak^2]/[k^2+2-k^2]=8a/2=4a 6、已知直线l:x=2p与抛物线 =2px(p>0)交于A、B两点,
求证:OA⊥OB.证明:由题意得,A(2p,2p),B(2p,-2p)
所以 =1, =-1
因此OA⊥OB变式1: 若直线l过定点(2p,0)且与抛物线 =2px(p>0)交于A、B两点,求证:OA⊥OB.变式2: 若直线l与抛物线 =2px(p>0)交于A、B两点,
且OA⊥OB ,则_____ _____. 直线l过定点(2p,0)高考链接:过定点Q(2p,0)的直线与
y2 = 2px(p>0)交于相异两点A、B,
以线段AB为直径作圆C(C为圆心),
试证明抛物线顶点在圆C上。 谢谢大家,再见!
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)关于x轴对称 关于x轴对称 关于y轴对称 关于y轴对称(0,0)(0,0)(0,0)(0,0)复习回顾:直线与圆、椭圆、双曲线的位置关系的判断方法:1、根据几何图形判断的直接判断2、直线与圆锥曲线的公共点的个数 形判断直线与双曲线位置关系的操作程序把直线方程代入双曲线方程得到一元一次方程得到一元二次方程直线与双曲线的
渐进线平行相交(一个交点) 计 算 判 别 式Fxy问题:你能说出直线与抛物线位置关系吗?二、讲授新课:判断直线与抛物线位置关系的操作程序:把直线方程代入抛物线方程得到一元一次方程得到一元二次方程直线与抛物线的
对称轴平行相交(一个交点) 计 算 判 别 式总结:例1、已知直线l:y=-x+1和抛物线
C:y2=4x,设直线与抛物线的交点为
A、B,求AB的长. 三、例题选讲:例2、已知抛物线C:y2=4x,设直线与抛物线两交点为A、B,且线段AB中点为M(2,1),求直线l的方程.说明:中点弦问题的解决方法:
①联立直线方程与曲线方程求解
②点差法1、求过定点(0,2),且与抛物线y2=4x相切的直线方程. 说明:(1)联立方程组,结合判别式求解
(2)注意斜率不存在的情形练习:1、在抛物线y2=64x上求一点,使它到直线L:4x+3y+46=0的距离最短,并求此距离.2、已知抛物线y=x2,动弦AB的长为2,求AB中点纵坐标的最小值.FABM解:解法二:FABM2、已知抛物线y=x2,动弦AB的长为2,求AB中点纵坐标的最小值.3、已知抛物线y2=2x,过Q(2,1)作直线与抛物线交于A、B,求AB中点的轨迹方程.解:焦点F(0,1/4a),准线y=-1/4a,设P(x1,y1),Q(x2,y2),
直线PQ:x=ky+k/4a 由抛物线第二定义, p=PF=y1+1/4a, q=PF2=y2+1/4a 联立y=ax^2,x=ky+k/4a, 得16a^2k^2y^2+(8ak^2-16a)y+k^2=0 ∴y1+y2=(16a-8ak^2)/16a^2k^2=(2-k^2)/2ak^2, y1y2=k^2/16a^2k^2=1/16a^2 1/p+1/q=1/(y1+1/4a)+1/(y2+1/4a)=[(y1+y2)+1/2a]/[y1y2+(y1+y2)/4a+1/16a^2] =[(2-k^2)/2ak^2+1/2a]/[1/16a^2+(2-k^2)/2ak^2/4a+1/16a^2](同乘8a^2k^2) =[4a(2-k^2)+4ak^2]/[k^2+2-k^2]=8a/2=4a 6、已知直线l:x=2p与抛物线 =2px(p>0)交于A、B两点,
求证:OA⊥OB.证明:由题意得,A(2p,2p),B(2p,-2p)
所以 =1, =-1
因此OA⊥OB变式1: 若直线l过定点(2p,0)且与抛物线 =2px(p>0)交于A、B两点,求证:OA⊥OB.变式2: 若直线l与抛物线 =2px(p>0)交于A、B两点,
且OA⊥OB ,则_____ _____. 直线l过定点(2p,0)高考链接:过定点Q(2p,0)的直线与
y2 = 2px(p>0)交于相异两点A、B,
以线段AB为直径作圆C(C为圆心),
试证明抛物线顶点在圆C上。 谢谢大家,再见!
