五年级上册数学教案-9.1 鸡兔同笼冀教版
文档属性
| 名称 | 五年级上册数学教案-9.1 鸡兔同笼冀教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 48.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 00:00:00 | ||
图片预览

文档简介
鸡兔同笼 教学设计
教学目标:
1.学习“鸡兔同笼”问题,感受古代数学的趣味性。
2. 经过探索过程解决问题,从而体验解决问题策略的多样化。在了解列表法的局限性后,体会假设法的简便之处。
3.在解决问题的过程中,培养学生的探索精神,逻辑推理能力以及应用数学知识解决实际问题的能力,并培养学生热爱数学学习的情感。
教学重点:应用假设法解决鸡兔同笼问题。
教学难点:理解假设法中头和脚的数量关系,能够清楚辨析“假设全是兔”和“假设全是鸡”时脚的数量以及多出和少算的脚的原理。
教学过程:
提出鸡兔同笼问题,让学生感受列表猜测法的局限性。
实际操练,学习假设法。
请一名女生扮演小兔子,一名男生扮演小公鸡。让学生观察此时头和脚的数量。
扮演兔子的女生需要伸出双手来表示有四只脚,扮演公鸡的男生需要背过两只手表示有两只脚。
当老师说假设全是鸡,女生把两只手臂收回去假装是鸡,表示只有两只脚。当老师说假设全是兔,那么男生则需要把手臂伸出表示有四只脚。
头 脚 脚与头的关系 和实际相差的脚 结论
开始 2 6
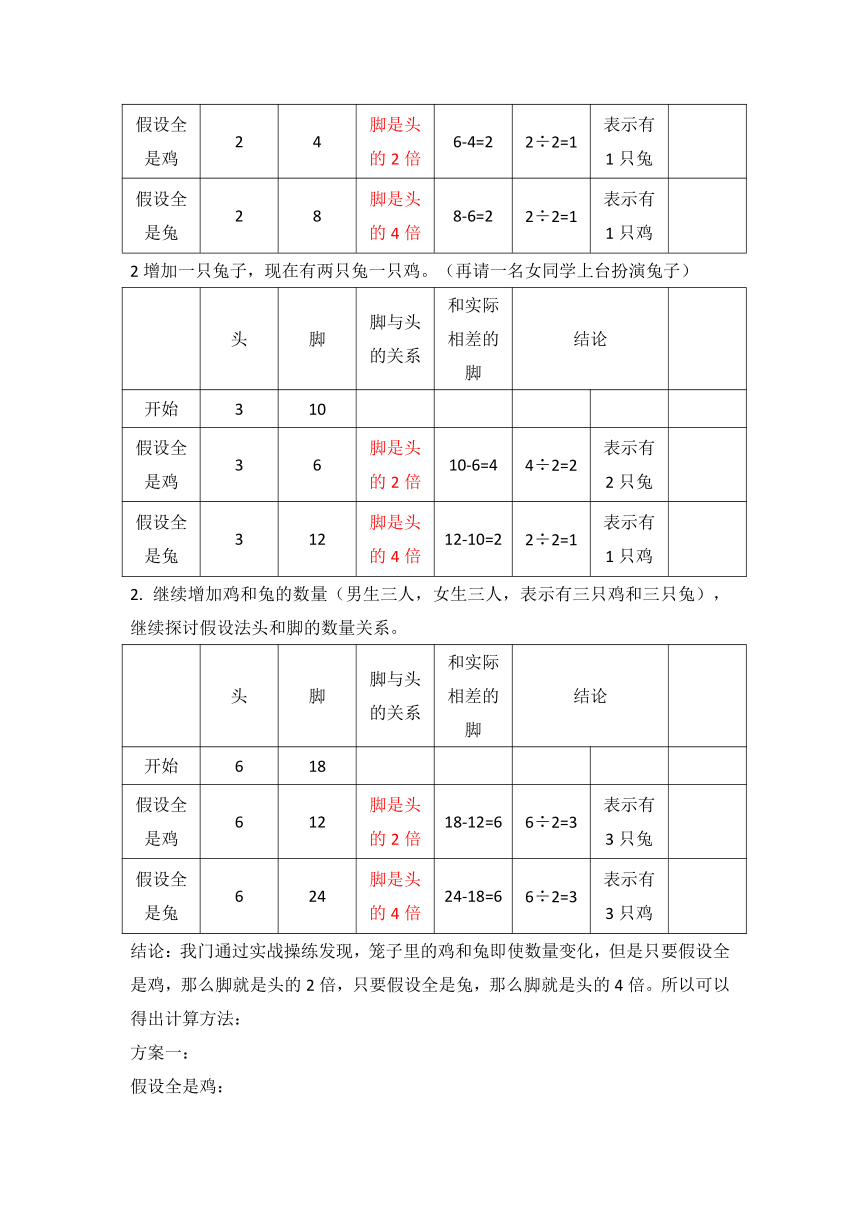
假设全是鸡 2 4 脚是头的2倍 6-4=2 2÷2=1 表示有1只兔
假设全是兔 2 8 脚是头的4倍 8-6=2 2÷2=1 表示有1只鸡
2增加一只兔子,现在有两只兔一只鸡。(再请一名女同学上台扮演兔子)
头 脚 脚与头的关系 和实际相差的脚 结论
开始 3 10
假设全是鸡 3 6 脚是头的2倍 10-6=4 4÷2=2 表示有2只兔
假设全是兔 3 12 脚是头的4倍 12-10=2 2÷2=1 表示有1只鸡
继续增加鸡和兔的数量(男生三人,女生三人,表示有三只鸡和三只兔),继续探讨假设法头和脚的数量关系。
头 脚 脚与头的关系 和实际相差的脚 结论
开始 6 18
假设全是鸡 6 12 脚是头的2倍 18-12=6 6÷2=3 表示有3只兔
假设全是兔 6 24 脚是头的4倍 24-18=6 6÷2=3 表示有3只鸡
结论:我门通过实战操练发现,笼子里的鸡和兔即使数量变化,但是只要假设全是鸡,那么脚就是头的2倍,只要假设全是兔,那么脚就是头的4倍。所以可以得出计算方法:
方案一:
假设全是鸡:
头×2=假设的脚
假设的脚与实际的脚求差,差是因为把兔子看成鸡,给每只兔子少算2只脚。
差÷2=兔子的数量
总数-兔子的数量=鸡的数量
方案二:
假设全是兔:
1.头×4=假设的脚
2.假设的脚与实际的脚求差,差是因为把鸡看成兔,给每只鸡多算2只脚。
3.差÷2=鸡的数量
4.总数-鸡的数量=兔的数量
解决问题
鸡兔同笼,从上面数有8个头,从下面数有26只脚,鸡兔各多少只?
解法一:假设笼子里全是鸡,
(26-8×2)÷2=5(只)
8-5=3(只)
兔有5只,鸡有3只。
解法二:假设笼子里全是兔,
(8×4-26)÷2=3(只)
8-3=5(只)
鸡有3只,兔有5只。
为古人解忧
假设笼子里全是鸡:(94-35×2)÷2=12(只) 35-12=23(只),兔有12只,鸡有23只。
假设笼子里全是兔:(35×4-94)÷2=23(只) 35-23=12(只),鸡有23只,兔有12只。
课后作业
盒子里有大小两种钢珠共30个 总共266g!大钢珠11g,小钢珠7g,大小钢珠各多少个?
板书设计
教学反思
鸡兔同笼问题是数学中学生比较容易出现问题的一个知识点,只有让学生深刻了解假设法的思维过程,才能把鸡兔同笼问题明白于心,牢记于心,所以课堂通过学生实际演练扮演鸡和兔,感受整个过程中头和脚的数量关系,使学生更清晰地明白假设法的运算过程。整个学习过程,也是一个培养兴趣的过程,让学生体会数学的乐趣,并能运用所学到的思维方法解决实际问题。
教学目标:
1.学习“鸡兔同笼”问题,感受古代数学的趣味性。
2. 经过探索过程解决问题,从而体验解决问题策略的多样化。在了解列表法的局限性后,体会假设法的简便之处。
3.在解决问题的过程中,培养学生的探索精神,逻辑推理能力以及应用数学知识解决实际问题的能力,并培养学生热爱数学学习的情感。
教学重点:应用假设法解决鸡兔同笼问题。
教学难点:理解假设法中头和脚的数量关系,能够清楚辨析“假设全是兔”和“假设全是鸡”时脚的数量以及多出和少算的脚的原理。
教学过程:
提出鸡兔同笼问题,让学生感受列表猜测法的局限性。
实际操练,学习假设法。
请一名女生扮演小兔子,一名男生扮演小公鸡。让学生观察此时头和脚的数量。
扮演兔子的女生需要伸出双手来表示有四只脚,扮演公鸡的男生需要背过两只手表示有两只脚。
当老师说假设全是鸡,女生把两只手臂收回去假装是鸡,表示只有两只脚。当老师说假设全是兔,那么男生则需要把手臂伸出表示有四只脚。
头 脚 脚与头的关系 和实际相差的脚 结论
开始 2 6
假设全是鸡 2 4 脚是头的2倍 6-4=2 2÷2=1 表示有1只兔
假设全是兔 2 8 脚是头的4倍 8-6=2 2÷2=1 表示有1只鸡
2增加一只兔子,现在有两只兔一只鸡。(再请一名女同学上台扮演兔子)
头 脚 脚与头的关系 和实际相差的脚 结论
开始 3 10
假设全是鸡 3 6 脚是头的2倍 10-6=4 4÷2=2 表示有2只兔
假设全是兔 3 12 脚是头的4倍 12-10=2 2÷2=1 表示有1只鸡
继续增加鸡和兔的数量(男生三人,女生三人,表示有三只鸡和三只兔),继续探讨假设法头和脚的数量关系。
头 脚 脚与头的关系 和实际相差的脚 结论
开始 6 18
假设全是鸡 6 12 脚是头的2倍 18-12=6 6÷2=3 表示有3只兔
假设全是兔 6 24 脚是头的4倍 24-18=6 6÷2=3 表示有3只鸡
结论:我门通过实战操练发现,笼子里的鸡和兔即使数量变化,但是只要假设全是鸡,那么脚就是头的2倍,只要假设全是兔,那么脚就是头的4倍。所以可以得出计算方法:
方案一:
假设全是鸡:
头×2=假设的脚
假设的脚与实际的脚求差,差是因为把兔子看成鸡,给每只兔子少算2只脚。
差÷2=兔子的数量
总数-兔子的数量=鸡的数量
方案二:
假设全是兔:
1.头×4=假设的脚
2.假设的脚与实际的脚求差,差是因为把鸡看成兔,给每只鸡多算2只脚。
3.差÷2=鸡的数量
4.总数-鸡的数量=兔的数量
解决问题
鸡兔同笼,从上面数有8个头,从下面数有26只脚,鸡兔各多少只?
解法一:假设笼子里全是鸡,
(26-8×2)÷2=5(只)
8-5=3(只)
兔有5只,鸡有3只。
解法二:假设笼子里全是兔,
(8×4-26)÷2=3(只)
8-3=5(只)
鸡有3只,兔有5只。
为古人解忧
假设笼子里全是鸡:(94-35×2)÷2=12(只) 35-12=23(只),兔有12只,鸡有23只。
假设笼子里全是兔:(35×4-94)÷2=23(只) 35-23=12(只),鸡有23只,兔有12只。
课后作业
盒子里有大小两种钢珠共30个 总共266g!大钢珠11g,小钢珠7g,大小钢珠各多少个?
板书设计
教学反思
鸡兔同笼问题是数学中学生比较容易出现问题的一个知识点,只有让学生深刻了解假设法的思维过程,才能把鸡兔同笼问题明白于心,牢记于心,所以课堂通过学生实际演练扮演鸡和兔,感受整个过程中头和脚的数量关系,使学生更清晰地明白假设法的运算过程。整个学习过程,也是一个培养兴趣的过程,让学生体会数学的乐趣,并能运用所学到的思维方法解决实际问题。
