9.1.2不等式的性质 课件（共35页）

(共35张PPT)
人教版 七年级下
精品同步教学课件
9.1 不等式
9.1.2 不等式的基本性质
课件栏目及使用说明：本课件适用于常规同步教学课堂，面向基础水平的学生使用。课件包括以下环节：
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
前面我们已经学习过等式的基本性质
（1）等式两边加（或减去）同一个数（或式子），
结果仍相等.
（2）等式两边乘同一个数，或除以同一个不为0的数，
结果仍相等.
猜想 ：不等式也具有同样的性质吗？
新知导入
探究：不等式的性质1
(1) 5>3, 5+2_____3+2, 5-2_____3-2;
(2) -1<3,-1+2_____3+2, -1-3______3-3;
观察并总结其中的规律。
＞
＞
＜
＜
用“>”或“<”填空
不等式的性质1：不等式两边加（或减）同一个数（或式子），不等号的方向不变.
如果a>b,那么a±c>b±c.
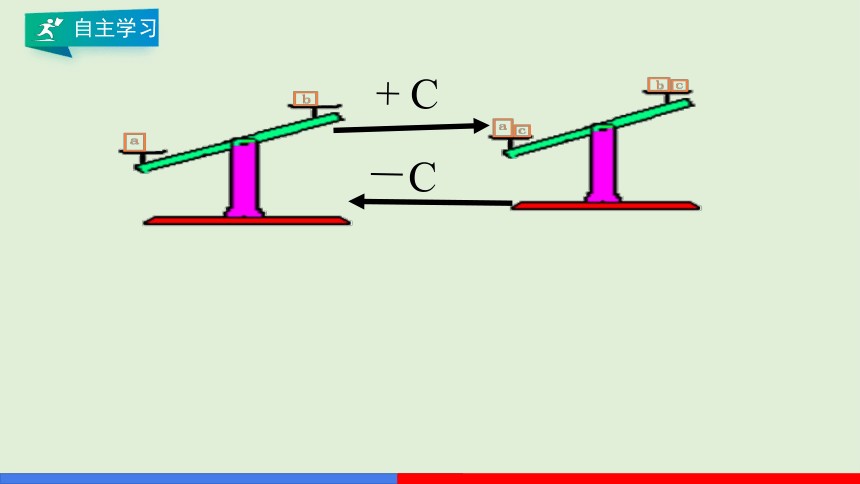
自主学习
+ C
－C
自主学习
探究：不等式的性质2
(3) 6>2, 6×5_____2×5, 6×_____2×;
(4) -2<3, (-2)×6_____3×6, (-2)×_____3×.
观察并总结其中的规律。
＞
＜
＜
＞
用“>”或“<”填空
不等式的性质2　不等式的两边都乘（或除以）同一个正数，不等号的方向不变.
即，如果a > b，c > 0，那么 ac > bc， > .
自主学习
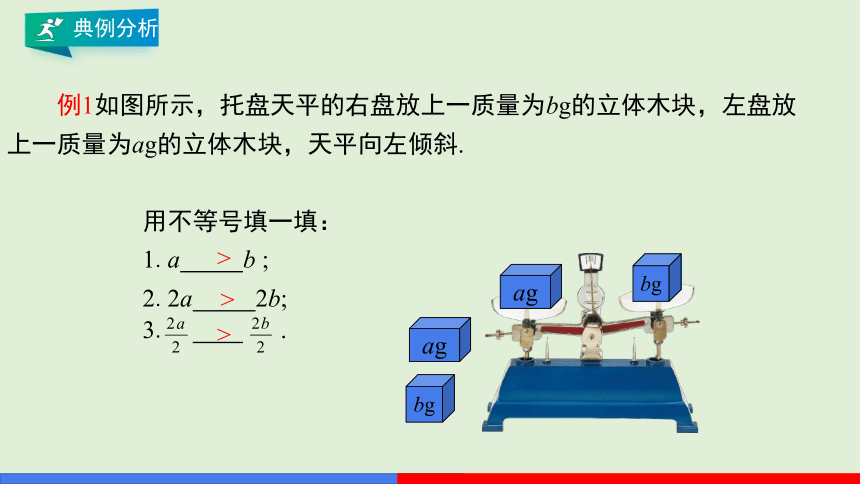
用不等号填一填：
1.a b ;
2.2a 2b;
3. .
例1如图所示，托盘天平的右盘放上一质量为bg的立体木块，左盘放上一质量为ag的立体木块，天平向左倾斜.
ag
bg
>
>
>
ag
bg
典例分析
探究：不等式的性质3
(5) 6>2,
6×（-5）_____2×（-5）, 6×_____2×;
(6) -2<3,
(-2)×（-6）_____3×（-6）, (-2)×_ 3×.
观察并总结其中的规律。
＞
＜
＜
＞
用“>”或“<”填空
不等式的性质3　不等式的两边都乘（或除以）同一个正数，不等号的方向不变.
自主学习
即，如果a > b，c < 0，那么 ac < bc， .
总结
不等式基本性质3 不等式的两边都乘（或除以）同一个负数，不等号的方向改变.
自主学习
1.不等式的对称性
如果x>y，那么y2.不等式的传递性
如果x>y，y>z；那么x>z；（传递性）
不等式的其他性质
如：8<10，10<15 ，8 15.
自主学习
（1）已知 a>b，则3a 3b ；
（2）已知 a>b，则-a -b .
>
<
用“>”或“<”填空：
例2
（3）已知 a>
典例分析
1.设a＞b，用“＜”“＞”填空并回答是根据不等式的
哪一条基本性质.
（1） a - 7____b - 7；
（2） a÷6____b÷6
（3） 0.1a____0.1b;
（4） -4a____-4b
（5） 2a+3____2b+3;
（6）(m2+1)a____ (m2+1)b(m为常数)
＞
＞
＞
＞
＞
＜
不等式的性质1
不等式的性质2
不等式的性质2
不等式的性质3
不等式的性质1,2
不等式的性质2
练一练
课堂练习
2.已知a＜0，用“＜”“＞”填空：
(1)a+2 ____2； (2)a-1 _____-1；
(3)3a______0； (4) ______0;
(5)a2_____0; (6)a3______0;
(7)a-1_____0； (8)|a|______0．
＜
＜
＜
＞
＜
＞
＜
＞
课堂练习
3.下列结论中正确的是(　　 )
A.由x≥5两边同乘1得x≥5
B.由x≥5两边同乘1得x≥5
C.由2x≥6两边同除以2得x≤3
D.由2x≥6两边同除以2得x≤3
D
课堂练习
拓展1
例1：利用不等式性质解不等式。
（1）x-7>26
（2）3x<2x+1
（3）x>50
（4）-4x>3
考点1：利用不等式性质解不等式
练习1.课后练习第1题
典例分析
考点2：含“≤”“≥”的不等式及应用
　　像a ≥ b或 a ≤ b这样的式子，也经常用来表示两个数量的大小关系.例如，某市某一天的最高气温是19最低气温是，我们可以用t表示这天的气温，t是随时间变化的，但是它有一定的变化范围，即t ≥ 并且t ≤ 19
“≥”读作“大于或等于”，也可说是“不小于”；“≤”读作“小于或等于”，也可说是“不大于”.
自主学习
例2铁路部门对随身携带的行李有如下规定：每件行李的长、宽、高之和不得超过160cm.设行李的长、宽、高分别为acm,bcm,ccm,请你列出行李的长、宽、高满足的关系式.
根据题意可得： a+b+c≤160.
典例分析
常用的表示不等关系的关键词语及对应的不等号
关 键 词 语 明确表明数量的不等关系 ①大 于 ②比…大 ③超 过 ①小 于 ②比…小 ③低 于 ①不小于 ②不低于 ③至 少 ①不大于
②不超过
③至 多
不 等 号
<
＞
≥
≤
自主学习
某长方体形状的容器长5cm,宽3cm,高10cm,容器内原有水的高度为3cm,现准备向它继续注水.用V(单位：cm3)表示新注入水的体积，写出V的取值范围.
例3
典例分析
解：新注入水的体积V与原有水的体积的和不能超过
容器的容积，即
V+3×5×3≤3×5×10
解得 V≤105
又由于新注入水的体积不能是负数，因此，V的取值范围是V≥0并且V≤105.
在数轴上表示V的取值范围如图所示.
0
105
典例分析
练习：用不等式表示下列语句并写出解集，并在数轴上表示解集.
（1）x的3倍大于或等于1；
（2）x与3的和不小于6；
（3）y与1的差不大于0；
（4）y的小于或等于-2.
课堂练习
解：(1)3x≥1, 解集是x≥ ;
(2)x+3≥6, 解集是x≥3;
(3)y-1≤0, 解集是y≤1;
0
3
0
1
0
-8
0
(4) y≤-2, 解集是y≤-8.
课堂练习
练习某次知识竞赛共有30道选择题答对一题得10分若不答或答错一道题则扣3分要使总得分不少于70分则应该至少答对几道题？若设答对x道题可列式子为( 　 )
A.10x3(30x)＞70
B.10x3(30x)≤70
C.10x3x≥70
D.10x3(30x)≥70
D
课堂练习
不等式的基本性质
不等式的基本性质2
不等式的基本性质3
→
→
如
那么
如果
那么
不等式的
基本性质1
如果a>b，那么a±c>b±c，
→
写出不等式的解集：
(1)x+2＞6；
(2)2x＜10；
(3)x－2＞0.1；
(4)－3x＜10.
1.
解：(1)x＞4；
(2)x＜5；
(3)x＞2.1；
(4)x＞ .
备选习题
设m＞n，用“＜”或“＞”填空：
(1)m－5 n－5； (2)m+4 n+4；
(3)6m 6n； (4) m n.
2.
＞
＞
＞
＜
备选习题
利用不等式的性质解下列不等式，并在数轴上表示解集：
(1)x+3＞－1；
3.
解：(1)根据不等式的性质1，不等式两边同时减去3，不等号方向不变，所以x+3－3＞－1－3，x＞－4.
在数轴上表示如图所示.
备选习题
(2)6x≤5x－7；
(2)根据不等式的性质1，不等式两边同时减去5x， 不等号方向不变，所以6x－5x≤5x－7－5x，得 x≤－7.
在数轴上表示如图所示.
备选习题
(3)
(3)根据不等式的性质3，不等式两边同时乘（－3），
不等号方向改变，所以 得 x＞－2.
在数轴上表示如图所示.
备选习题
(4)4x≥－12；
(4)根据不等式的性质3，不等式两边同时除以4，不等号方向不变，所以x≥－3.
在数轴上表示如图所示.
备选习题
设a＞b，用“＜”或“＞”填空：
(1)2a－5 2b－5；
(2)－3.5b+1 －3.5a+1.
4.
＞
＞
备选习题
根据机器零件的设计图纸(如图)，用不等式表示零件长度的合格尺寸(L的取值范围).
5.
解：由题意得，40－0.02≤L≤40+0.02，
即39.98≤L≤40.02.
备选习题
https://www.21cnjy.com/help/help_extract.php