9.2.2一元一次不等式应用 课件(共28页)
文档属性
| 名称 | 9.2.2一元一次不等式应用 课件(共28页) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
人教版 七年级下
精品同步教学课件
9.1 不等式
9.2.2一元一次不等式应用
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
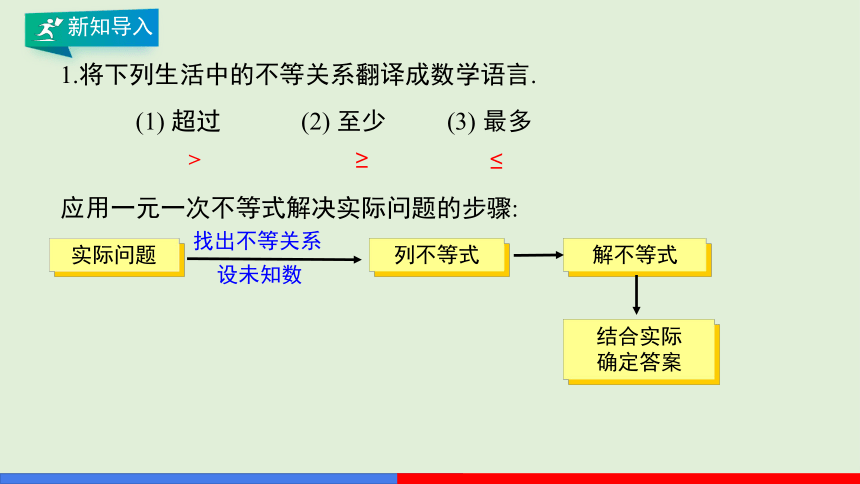
1.将下列生活中的不等关系翻译成数学语言.
(1) 超过
(2) 至少
(3) 最多
>
≥
≤
应用一元一次不等式解决实际问题的步骤:
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
新知导入
一次党史知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分.在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
解: 设小明答对了 x 道题,则他答错和不答
的共有 (25-x)道题.根据题意,得
4x-1×(25-x)≥85.
解这个不等式,得 x ≥ 22.
例1
所以,小明至少答对了22道题.
练习:P125第2题
典例分析
去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数比去年至少要增加多少?
例2
分析:“明年这样的比值要超过70%”指出了这个
问题中蕴含的不等关系,转化为不等式,即
>70%.
明年空气质量好的天数
明年天数
解: 设明年比去年空气质量良好的天数增加x天.
解得 x>36.5.
答:明年空气质量良好的天数比去年至少要增加37天,才能使这一年空气质量良好的天数超过全年天数的70%.
由x 应为正整数,得 x≥37.
>70%.
x+365×60%
365
去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数比去年至少要增加多少?
设明年比去年空气质量良好的天数增加了x天,
依题意,得x+365×60%>365×70%
解这个不等式,得x>36.56.
由x应为正整数,得x≥37
答:明年空气质量良好的天数比去年至少要增加37,才能使这一年空气质量良好的天数超过全年天数的70%.
去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数比去年至少要增加多少?
列一元一次不等式解应用题的基本步骤与列一元一次方程解应用题的步骤相类似,即
(1)审题:认真审题,分清已知量、未知量;
(2)设未知数:设出适当的未知数;
(3)列不等式:根据题中的不等关系列出不等式;
(4)解不等式:解所列的不等式;
(6)答:写出答案
总结
(5)验:检验是否符合题意
解:设小明家每月用水x立方米.
∵5×1.8=9<15,
∴小明家每月用水超过5立方米,
则超出(x-5)立方米,按每立方米2元收费,
列出不等式为:5×1.8+(x-5)×2≥15,
解不等式得:x≥8.
答:小明家每月用水量至少是8立方米.
例3 小明家每月水费都不少于15元,自来水公司的收费标准如下:若每户每月用水不超过5立方米,则每立方米收费1.8元;若每户每月用水超过5立方米,则超出部分每立方米收费2元,小明家每月用水量至少是多少?
典例分析
练习:某市打市内电话的收费标准是:每次3 min以内(含3 min)0.22元,以后每分钟0.11元(不足1 min部分按1 min计).小琴一天在家里给同学打了一次市内电话,所用电话费没超过0.5元.她最多打了几分钟的电话?
解:设小琴打了x分钟的电话,根据题意,得
0.22+ (x-3) ×0.11≤0.5
解得 x ≤5.5
由于电话计时按照分钟计时,x应是整数,所以x的最大值为5.
小琴最多打了5min的电话.
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费,设王老师在同一商场累计购物x元,其中x>100.
例4
(1)根据题意,填写下表(单位:元):
累计购 实际花费 130 290 … x
在甲商场 127 …
在乙商场 126 …
0.95x+2.5
0.9x+10
271
278
典例分析
例4
(2)当x取何值时,王老师在甲、乙两商场的实际花费相同?
解:根据题意得:
0.9x+10=0.95x+2.5,
解得:x=150,
∴当x=150时,王老师在甲、乙两商场的实际花费相同
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费,设王老师在同一商场累计购物x元,其中x>100.
典例分析
例4
(3)当王老师在同一商场累计购物超过100元时,在哪家商场的实际花费少?
根据题意得:
0.9x+10<0.95x+2.5,解得:x>150,
0.9x+10>0.95x+2.5,解得:x<150,
则当王老师累计购物大于150时,选择甲商场实际花费少;
当累计购物正好为150元时,两商场花费相同;
当王老师累计购物超过100元而不到150元时,在乙商场实际花费少.
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费,设王老师在同一商场累计购物x元,其中x>100.
典例分析
分析:甲乙两商场的优惠价格不一样,因此需要分类讨论:
(1)当购物不超过50元;
(2)当购物超过50元而不超过100元,
(3)当购物超过100元.
变式
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
典例分析
解:(1)当购物不超过50元时,在甲、乙两商场都不享受优惠,购物花费一样;
(2)当购物超过50元而不超过100元时,在乙商场享受优惠, 购物花费少;
(3)当累计购物超过100元后,设购物为x(x>100)元
①若到甲商场购物花费少,则 50+0.95(x-50)>100+0.9(x-100) ,
解得x>150. 所以累计购物超过150元时,到甲商场购物花费少;
②若到乙商场购物花费少, 则 50+0.95(x-50)<100+0.9(x-100) ,
解得x<150.所以累计购物超过100元而不到100元时,到乙商场购物花费少;
③若 50+0.95(x-50)=100+0.9(x-100) ,解得x=150.
所以累计购物为150元时,到甲、乙两商场购物花费一样.
典例分析
甲、乙两家超市以相同的价格出售同样的商品时,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价9折优惠.设顾客预计累计购物x元(x>300).
(1)请用含x的代数式分别表示顾客在两家超市购物所付的费用;
解:
(1)在甲超市购物所付的费用为:300+0.8(x-300)=0.8x+60,
在乙超市购物所付的费用为:200+0.9(x-200)=0.9x+20;
典例分析
甲、乙两家超市以相同的价格出售同样的商品时,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价9折优惠.设顾客预计累计购物x元(x>300).
(2)如果两位顾客分别预计购物350元、600元时,试比较顾客到哪家超市购物更优惠?
解:当购物为350元时,在甲超市购物所付的费用为:300+0.8×(350-300)=340(元),在乙超市购物所付的费用为:200+0.9×(350-200)=335(元),所以在乙超市购物更优惠;
当购物为600元时,在甲超市购物所付的费用为:300+0.8×(600-300)=540(元),在乙超市购物所付的费用为:200+0.9×(600-200)=560(元),所以在甲超市购物更优惠;
典例分析
甲、乙两家超市以相同的价格出售同样的商品时,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价9折优惠.设顾客预计累计购物x元(x>300).
(3)想一想,你还能提出什么问题?
解:当0.8x+60=0.9x+20时,解得:x=400,∴当x=400元时,两家超市一样;
当0.8x+60<0.9x+20时,解得:x>400,当x>400元时,甲超市更合算;
当0.8x+60>0.9x+20时,解得:x<400,当x<400元时,乙超市更合算,
问题1:在哪家超市购物更合算?
典例分析
练习:几位同学参加周末郊游.甲旅行社说:“只要一名学生买全票,则其余学生可享受半价优惠.”乙旅行社说:“所有学生都可按6折优惠.”已知全票价为240元.
(1)设学生人数为x,甲旅行社收费为y甲元,乙旅行社收费为y乙元.写出x与y甲,x与y乙的关系式.
(2)就学生人数x讨论哪一家旅行社更优惠?
课堂练习
(1)y甲=240+120(x-1), y乙=144x.
(2) 当y甲=y乙时: ,化简整理得24x=120,即 x=5,所以人数等于5人时任选一家旅行社;
当y甲>y乙时: ,化简整理得,24x<120,即 x<5.所以人数少于5人时选乙旅行社;
当y甲120,即 x>5,所以人数多于5人时选甲旅行社.
课堂练习
某商店以每辆250元的进价购入200辆自行车,并以每辆275元的价格销售. 两个月后自行车的销售款已超过这批自行车的进货款,这时至少已售出多少辆自行车?
1.
解:设已售出x辆自行车. 由题意,得
275x>250×200,解得x>181.8.
因为x为整数,所以x≥182,且x为整数.
答:这时至少已售出182辆自行车.
备选习题
长跑比赛中,张华跑在前面,在离终点100 m时他以4 m/s的速度向终点冲刺,在他身后10 m的李明需以多快的速度同时开始冲刺,才能够在张华之前到达终点?
2.
备选习题
解:设李明以x m/s的速度冲刺,
由题意,得
因为x是正数,不等式两边乘4x,不等号方向不变,所以100x>440,所以x>4.4.
答:李明需以超过4.4 m/s的速度冲刺,才能在张华之前到达终点.
备选习题
某工厂前年有员工280人,去年经过结构改革减员40人,全厂年利润增加100万元,人均创利至少增加6000元,前年全厂年利润至少是多少?
3.
解:设前年全厂年利润为x万元,根据题意,得
解得x≥308.
答:前年全厂利润至少为308万元.
备选习题
苹果的进价是每千克1.5元,销售中估计有5%的苹果正常损耗. 商家把售价至少定为多少,才能避免亏本?
4.
解:设商家把售价定为x元/千克,根据题意,得
(1-5%)x≥1.5,解得x≥
答:商家把售价至少定为 元/千克,才能避免亏本.
备选习题
电脑公司销售一批计算机,第一个月以5500元/台的价格售出60台,第二个月起降价,以5000元/台的价格将这批计算机全部售出,销售总额超过55万元.这批计算机最少有多少台?
5.
解:设这批计算机有x台,根据题意,得
5500×60+5000(x-60)>550000,解得x>104.
答:这批计算机最少有105台.
备选习题
https://www.21cnjy.com/help/help_extract.php
人教版 七年级下
精品同步教学课件
9.1 不等式
9.2.2一元一次不等式应用
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
1.将下列生活中的不等关系翻译成数学语言.
(1) 超过
(2) 至少
(3) 最多
>
≥
≤
应用一元一次不等式解决实际问题的步骤:
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
新知导入
一次党史知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分.在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
解: 设小明答对了 x 道题,则他答错和不答
的共有 (25-x)道题.根据题意,得
4x-1×(25-x)≥85.
解这个不等式,得 x ≥ 22.
例1
所以,小明至少答对了22道题.
练习:P125第2题
典例分析
去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数比去年至少要增加多少?
例2
分析:“明年这样的比值要超过70%”指出了这个
问题中蕴含的不等关系,转化为不等式,即
>70%.
明年空气质量好的天数
明年天数
解: 设明年比去年空气质量良好的天数增加x天.
解得 x>36.5.
答:明年空气质量良好的天数比去年至少要增加37天,才能使这一年空气质量良好的天数超过全年天数的70%.
由x 应为正整数,得 x≥37.
>70%.
x+365×60%
365
去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数比去年至少要增加多少?
设明年比去年空气质量良好的天数增加了x天,
依题意,得x+365×60%>365×70%
解这个不等式,得x>36.56.
由x应为正整数,得x≥37
答:明年空气质量良好的天数比去年至少要增加37,才能使这一年空气质量良好的天数超过全年天数的70%.
去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数比去年至少要增加多少?
列一元一次不等式解应用题的基本步骤与列一元一次方程解应用题的步骤相类似,即
(1)审题:认真审题,分清已知量、未知量;
(2)设未知数:设出适当的未知数;
(3)列不等式:根据题中的不等关系列出不等式;
(4)解不等式:解所列的不等式;
(6)答:写出答案
总结
(5)验:检验是否符合题意
解:设小明家每月用水x立方米.
∵5×1.8=9<15,
∴小明家每月用水超过5立方米,
则超出(x-5)立方米,按每立方米2元收费,
列出不等式为:5×1.8+(x-5)×2≥15,
解不等式得:x≥8.
答:小明家每月用水量至少是8立方米.
例3 小明家每月水费都不少于15元,自来水公司的收费标准如下:若每户每月用水不超过5立方米,则每立方米收费1.8元;若每户每月用水超过5立方米,则超出部分每立方米收费2元,小明家每月用水量至少是多少?
典例分析
练习:某市打市内电话的收费标准是:每次3 min以内(含3 min)0.22元,以后每分钟0.11元(不足1 min部分按1 min计).小琴一天在家里给同学打了一次市内电话,所用电话费没超过0.5元.她最多打了几分钟的电话?
解:设小琴打了x分钟的电话,根据题意,得
0.22+ (x-3) ×0.11≤0.5
解得 x ≤5.5
由于电话计时按照分钟计时,x应是整数,所以x的最大值为5.
小琴最多打了5min的电话.
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费,设王老师在同一商场累计购物x元,其中x>100.
例4
(1)根据题意,填写下表(单位:元):
累计购 实际花费 130 290 … x
在甲商场 127 …
在乙商场 126 …
0.95x+2.5
0.9x+10
271
278
典例分析
例4
(2)当x取何值时,王老师在甲、乙两商场的实际花费相同?
解:根据题意得:
0.9x+10=0.95x+2.5,
解得:x=150,
∴当x=150时,王老师在甲、乙两商场的实际花费相同
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费,设王老师在同一商场累计购物x元,其中x>100.
典例分析
例4
(3)当王老师在同一商场累计购物超过100元时,在哪家商场的实际花费少?
根据题意得:
0.9x+10<0.95x+2.5,解得:x>150,
0.9x+10>0.95x+2.5,解得:x<150,
则当王老师累计购物大于150时,选择甲商场实际花费少;
当累计购物正好为150元时,两商场花费相同;
当王老师累计购物超过100元而不到150元时,在乙商场实际花费少.
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费,设王老师在同一商场累计购物x元,其中x>100.
典例分析
分析:甲乙两商场的优惠价格不一样,因此需要分类讨论:
(1)当购物不超过50元;
(2)当购物超过50元而不超过100元,
(3)当购物超过100元.
变式
甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
典例分析
解:(1)当购物不超过50元时,在甲、乙两商场都不享受优惠,购物花费一样;
(2)当购物超过50元而不超过100元时,在乙商场享受优惠, 购物花费少;
(3)当累计购物超过100元后,设购物为x(x>100)元
①若到甲商场购物花费少,则 50+0.95(x-50)>100+0.9(x-100) ,
解得x>150. 所以累计购物超过150元时,到甲商场购物花费少;
②若到乙商场购物花费少, 则 50+0.95(x-50)<100+0.9(x-100) ,
解得x<150.所以累计购物超过100元而不到100元时,到乙商场购物花费少;
③若 50+0.95(x-50)=100+0.9(x-100) ,解得x=150.
所以累计购物为150元时,到甲、乙两商场购物花费一样.
典例分析
甲、乙两家超市以相同的价格出售同样的商品时,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价9折优惠.设顾客预计累计购物x元(x>300).
(1)请用含x的代数式分别表示顾客在两家超市购物所付的费用;
解:
(1)在甲超市购物所付的费用为:300+0.8(x-300)=0.8x+60,
在乙超市购物所付的费用为:200+0.9(x-200)=0.9x+20;
典例分析
甲、乙两家超市以相同的价格出售同样的商品时,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价9折优惠.设顾客预计累计购物x元(x>300).
(2)如果两位顾客分别预计购物350元、600元时,试比较顾客到哪家超市购物更优惠?
解:当购物为350元时,在甲超市购物所付的费用为:300+0.8×(350-300)=340(元),在乙超市购物所付的费用为:200+0.9×(350-200)=335(元),所以在乙超市购物更优惠;
当购物为600元时,在甲超市购物所付的费用为:300+0.8×(600-300)=540(元),在乙超市购物所付的费用为:200+0.9×(600-200)=560(元),所以在甲超市购物更优惠;
典例分析
甲、乙两家超市以相同的价格出售同样的商品时,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价9折优惠.设顾客预计累计购物x元(x>300).
(3)想一想,你还能提出什么问题?
解:当0.8x+60=0.9x+20时,解得:x=400,∴当x=400元时,两家超市一样;
当0.8x+60<0.9x+20时,解得:x>400,当x>400元时,甲超市更合算;
当0.8x+60>0.9x+20时,解得:x<400,当x<400元时,乙超市更合算,
问题1:在哪家超市购物更合算?
典例分析
练习:几位同学参加周末郊游.甲旅行社说:“只要一名学生买全票,则其余学生可享受半价优惠.”乙旅行社说:“所有学生都可按6折优惠.”已知全票价为240元.
(1)设学生人数为x,甲旅行社收费为y甲元,乙旅行社收费为y乙元.写出x与y甲,x与y乙的关系式.
(2)就学生人数x讨论哪一家旅行社更优惠?
课堂练习
(1)y甲=240+120(x-1), y乙=144x.
(2) 当y甲=y乙时: ,化简整理得24x=120,即 x=5,所以人数等于5人时任选一家旅行社;
当y甲>y乙时: ,化简整理得,24x<120,即 x<5.所以人数少于5人时选乙旅行社;
当y甲
课堂练习
某商店以每辆250元的进价购入200辆自行车,并以每辆275元的价格销售. 两个月后自行车的销售款已超过这批自行车的进货款,这时至少已售出多少辆自行车?
1.
解:设已售出x辆自行车. 由题意,得
275x>250×200,解得x>181.8.
因为x为整数,所以x≥182,且x为整数.
答:这时至少已售出182辆自行车.
备选习题
长跑比赛中,张华跑在前面,在离终点100 m时他以4 m/s的速度向终点冲刺,在他身后10 m的李明需以多快的速度同时开始冲刺,才能够在张华之前到达终点?
2.
备选习题
解:设李明以x m/s的速度冲刺,
由题意,得
因为x是正数,不等式两边乘4x,不等号方向不变,所以100x>440,所以x>4.4.
答:李明需以超过4.4 m/s的速度冲刺,才能在张华之前到达终点.
备选习题
某工厂前年有员工280人,去年经过结构改革减员40人,全厂年利润增加100万元,人均创利至少增加6000元,前年全厂年利润至少是多少?
3.
解:设前年全厂年利润为x万元,根据题意,得
解得x≥308.
答:前年全厂利润至少为308万元.
备选习题
苹果的进价是每千克1.5元,销售中估计有5%的苹果正常损耗. 商家把售价至少定为多少,才能避免亏本?
4.
解:设商家把售价定为x元/千克,根据题意,得
(1-5%)x≥1.5,解得x≥
答:商家把售价至少定为 元/千克,才能避免亏本.
备选习题
电脑公司销售一批计算机,第一个月以5500元/台的价格售出60台,第二个月起降价,以5000元/台的价格将这批计算机全部售出,销售总额超过55万元.这批计算机最少有多少台?
5.
解:设这批计算机有x台,根据题意,得
5500×60+5000(x-60)>550000,解得x>104.
答:这批计算机最少有105台.
备选习题
https://www.21cnjy.com/help/help_extract.php
