2022年华东师大版七年级下册数学 9.1.2 三角形的内角和与外角和教案
文档属性
| 名称 | 2022年华东师大版七年级下册数学 9.1.2 三角形的内角和与外角和教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 56.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 20:17:04 | ||
图片预览

文档简介
三角形的内角和(一)教案
教学目标:
1.知道三角形内角之间的关系,直角三角形的两个内角互余
2.能运用相关结论进行有关的推理和计算;
教学难点
探索三角形3个内角之间的关系
2.灵活使用相关结论,理性思维的培养
教学过程
一、创设情境,感悟三角形内角和等于1800
在小学里,学生知道三角形内角和等于1800 ,通过运用几何画版制作的课件,使学生直观地感受三角形的三个内角之间的关系。
情境1:感受△ABC的形状在不断变化过程中三角形三内角的和为1800。
情境2:感受△ABC用拼图的方法得出三角形内角和等于1800 。
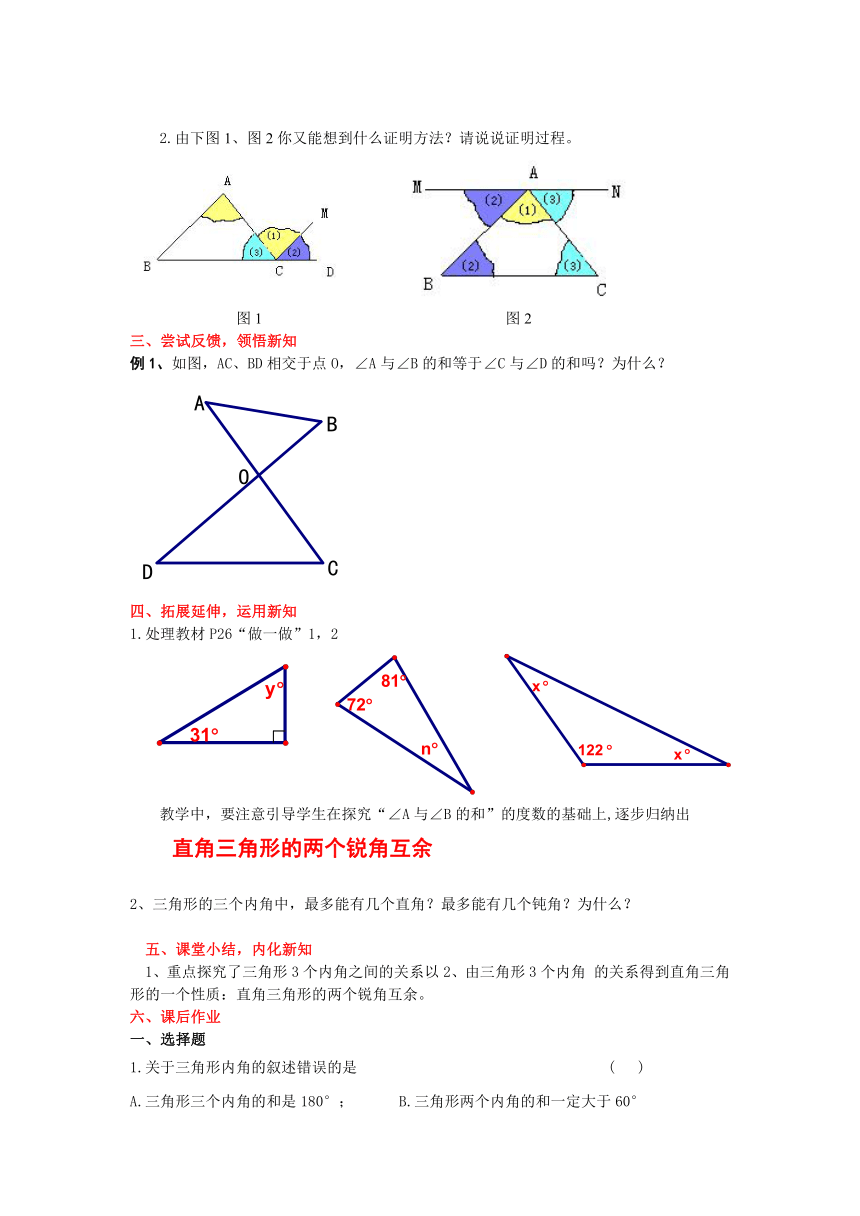
方法一,在△ABC中,把∠A撕下,然后把点A与点C重合在同一点,摆成如图所示的位置。
方法二,其它拼图验证方法(如集中在A点)
二、探索规律,揭示三角形内角和等于1800
1.议一议:如图7-33,3根木条相交成∠1,∠2,若木条a与木条b平行,则∠1+∠2=1800
操作:把木条a绕点A转动,使它与木条b相交于点C,根据图(2),你能说明“三角形内角和等于1800”吗?
三角形内角和定理:三角形的内角和等于1800
2.由下图1、图2你又能想到什么证明方法?请说说证明过程。
图1 图2
三、尝试反馈,领悟新知
例1、如图,AC、BD相交于点O,∠A与∠B的和等于∠C与∠D的和吗?为什么?
四、拓展延伸,运用新知
1.处理教材P26“做一做”1,2
教学中,要注意引导学生在探究“∠A与∠B的和”的度数的基础上,逐步归纳出
直角三角形的两个锐角互余
2、三角形的三个内角中,最多能有几个直角?最多能有几个钝角?为什么?
五、课堂小结,内化新知
1、重点探究了三角形3个内角之间的关系以2、由三角形3个内角 的关系得到直角三角形的一个性质:直角三角形的两个锐角互余。
六、课后作业
一、选择题
1.关于三角形内角的叙述错误的是 ( )
A.三角形三个内角的和是180°; B.三角形两个内角的和一定大于60°
C.三角形中至少有一个角不小于60°; D.一个三角形中最大的角所对的边最长
2.下列叙述正确的是 ( )
A.钝角三角形的内角和大于锐角三角形的内角和;
B.三角形两个内角的和一定大于第三个内角;
C.三角形中至少有两个锐角; D.三角形中至少有一个锐角。
3.三角形中最大的内角一定是 ( )
A.钝角 B.直角; C.大于60°的角 D.大于等于60°的角
4. 在△ABC中,∠ABC和∠ACB的平分线交于点O,下列计算中错误的是( )
A.若∠ABC=50°,∠ACB=80°,则∠BOC=115°;
B.若∠ABC+∠ACB=120°,则∠BOC=120°;
C.若∠A=90°,则∠BOC=135°;
D.若∠BOC=100°,则∠A=50°
5. 三角形的一个外角小于和它相邻的内角,则此三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
二、填空题
6.如图(1),在△ABC中,∠BAC=90°,AD⊥BC于D,则∠B=∠________,∠C=∠________.
7. 在△ABC中,∠A+∠B=120°,∠A-∠B+∠C=120°,则∠A=_______,∠B=______.
8. 如图(2),∠______是△ABD的外角,∠____是△BCE的外角,若∠DEC=60°,
∠ECB=40°,则∠DBC=_______.
(1) (2)
9. 如图1-41所示.∠A=10°,∠ABC=90°,∠ACB=∠DCE,
∠ADC=∠EDF,∠CED=∠FEG.则∠F=____________.
10.如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=42°,∠C=70°,
∠DAE=____________.
三、解答题:
11.如图,在△ABC中,CD平分∠ACB,DE∥AC,∠B=72°,∠EDC=36°,求∠ADC的大小.
12.如图,在△ABC中,P是AB上一点,D是CB的延长线上一点.求证:∠APC>∠BPD.
13.已知∠ABC,∠ACB的平分线交于I。
(1)根据下列条件分别求出∠BIC的度数:①∠ABC=70°,∠ACB=50°;②∠ACB+∠ABC=120°;③∠A=90°;④∠A=n°;
(2)你能发现∠BIC与∠A的关系吗?
14.如图,已知在△ABC中,BD平分∠ABC,CD平分△ABC的外角∠ACE,BD、CD相交于D,试说明∠A=2∠D的理由.
教学目标:
1.知道三角形内角之间的关系,直角三角形的两个内角互余
2.能运用相关结论进行有关的推理和计算;
教学难点
探索三角形3个内角之间的关系
2.灵活使用相关结论,理性思维的培养
教学过程
一、创设情境,感悟三角形内角和等于1800
在小学里,学生知道三角形内角和等于1800 ,通过运用几何画版制作的课件,使学生直观地感受三角形的三个内角之间的关系。
情境1:感受△ABC的形状在不断变化过程中三角形三内角的和为1800。
情境2:感受△ABC用拼图的方法得出三角形内角和等于1800 。
方法一,在△ABC中,把∠A撕下,然后把点A与点C重合在同一点,摆成如图所示的位置。
方法二,其它拼图验证方法(如集中在A点)
二、探索规律,揭示三角形内角和等于1800
1.议一议:如图7-33,3根木条相交成∠1,∠2,若木条a与木条b平行,则∠1+∠2=1800
操作:把木条a绕点A转动,使它与木条b相交于点C,根据图(2),你能说明“三角形内角和等于1800”吗?
三角形内角和定理:三角形的内角和等于1800
2.由下图1、图2你又能想到什么证明方法?请说说证明过程。
图1 图2
三、尝试反馈,领悟新知
例1、如图,AC、BD相交于点O,∠A与∠B的和等于∠C与∠D的和吗?为什么?
四、拓展延伸,运用新知
1.处理教材P26“做一做”1,2
教学中,要注意引导学生在探究“∠A与∠B的和”的度数的基础上,逐步归纳出
直角三角形的两个锐角互余
2、三角形的三个内角中,最多能有几个直角?最多能有几个钝角?为什么?
五、课堂小结,内化新知
1、重点探究了三角形3个内角之间的关系以2、由三角形3个内角 的关系得到直角三角形的一个性质:直角三角形的两个锐角互余。
六、课后作业
一、选择题
1.关于三角形内角的叙述错误的是 ( )
A.三角形三个内角的和是180°; B.三角形两个内角的和一定大于60°
C.三角形中至少有一个角不小于60°; D.一个三角形中最大的角所对的边最长
2.下列叙述正确的是 ( )
A.钝角三角形的内角和大于锐角三角形的内角和;
B.三角形两个内角的和一定大于第三个内角;
C.三角形中至少有两个锐角; D.三角形中至少有一个锐角。
3.三角形中最大的内角一定是 ( )
A.钝角 B.直角; C.大于60°的角 D.大于等于60°的角
4. 在△ABC中,∠ABC和∠ACB的平分线交于点O,下列计算中错误的是( )
A.若∠ABC=50°,∠ACB=80°,则∠BOC=115°;
B.若∠ABC+∠ACB=120°,则∠BOC=120°;
C.若∠A=90°,则∠BOC=135°;
D.若∠BOC=100°,则∠A=50°
5. 三角形的一个外角小于和它相邻的内角,则此三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
二、填空题
6.如图(1),在△ABC中,∠BAC=90°,AD⊥BC于D,则∠B=∠________,∠C=∠________.
7. 在△ABC中,∠A+∠B=120°,∠A-∠B+∠C=120°,则∠A=_______,∠B=______.
8. 如图(2),∠______是△ABD的外角,∠____是△BCE的外角,若∠DEC=60°,
∠ECB=40°,则∠DBC=_______.
(1) (2)
9. 如图1-41所示.∠A=10°,∠ABC=90°,∠ACB=∠DCE,
∠ADC=∠EDF,∠CED=∠FEG.则∠F=____________.
10.如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=42°,∠C=70°,
∠DAE=____________.
三、解答题:
11.如图,在△ABC中,CD平分∠ACB,DE∥AC,∠B=72°,∠EDC=36°,求∠ADC的大小.
12.如图,在△ABC中,P是AB上一点,D是CB的延长线上一点.求证:∠APC>∠BPD.
13.已知∠ABC,∠ACB的平分线交于I。
(1)根据下列条件分别求出∠BIC的度数:①∠ABC=70°,∠ACB=50°;②∠ACB+∠ABC=120°;③∠A=90°;④∠A=n°;
(2)你能发现∠BIC与∠A的关系吗?
14.如图,已知在△ABC中,BD平分∠ABC,CD平分△ABC的外角∠ACE,BD、CD相交于D,试说明∠A=2∠D的理由.
