人教版 六年级数学下册 3.2.2 圆锥的体积 课件 (共16张PPT)
文档属性
| 名称 | 人教版 六年级数学下册 3.2.2 圆锥的体积 课件 (共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 19:36:55 | ||
图片预览






文档简介
(共16张PPT)
3.2.2圆锥的体积
1、引导学生通过观看实验,推导出圆锥体积的计算公式;并能运用计算公式求圆锥的体积。
2、培养 学生的观察、操作、分析表达,归纳概括能力。
3、培养学生良好的学习兴趣。
教学目标
V=abc
V=a3
一、复习旧知
圆柱公式复习
V柱=πr2h
圆柱
圆锥
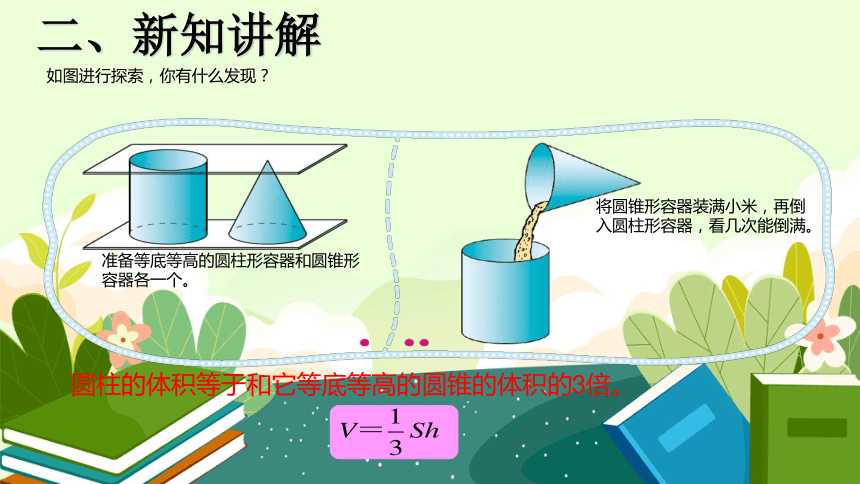
准备等底等高的圆柱形容器和圆锥形容器各一个。
将圆锥形容器装满小米,再倒入圆柱形容器,看几次能倒满。
圆柱的体积等于和它等底等高的圆锥的体积的3倍。
如图进行探索,你有什么发现?
二、新知讲解
我们已经会计算圆柱的体积,如何计算圆锥的体积呢?
圆锥的体积和圆柱的体积有没有关系呢?
圆柱的底面是圆,圆锥的底面也是圆……
圆锥的体积=底面积×高× ,
用字母表示为V= Sh。
有一堆小米,近似于圆锥形,量得
底面周长是9.31厘米,高4厘米。
求它的体积?
1、计算下面各圆锥的体积。
三、小刀试牛
2、如图,测量中经常使用铅锤。这个铅锤的体积是
多少立方厘米?
≈26.17(cm3)
3、一个用钢铸造成的圆锥形铅锤,底面直径是4cm,
高5cm。每立方厘米钢大约重7.8g。这个铅锤重
多少克?(得数保留整数)
3
1
(2)铅锤的体积:
(1)铅锤底面积:
21×7.8≈164(g)
(3)铅锤的质量:
答:这个铅锤大约重164g。
×12.56×5≈21(cm3)
3.14×( )=3.14×4=12.56(cm2)
2
4
2
(1)一个圆柱的体积是75.36m3,与它等底等高的圆锥的体积是( )m3。
25.12
(2)一个圆锥的体积是141.3m3,与它等底等高的圆柱的体积是( )m3。
423.9
141.3×3=423.9(m3)
四、课堂练习
75.36× =25.12(m3)
3
1
1、填空题
2、 一个圆锥形沙堆,底面积是28.26m2,高是2.5m。用这堆
沙在10m宽的公路上铺2cm厚的路面,能铺多少米?
2cm=0.02m
(1)沙堆的体积:
=9.42×2.5
=23.55(m3)
23.55÷10÷0.02
=2.355÷0.02
=117.75(m)
(2)所铺公路的长度
答:能铺117.75m。
×28.26×2.5
3
1
请你想一想,转换前后沙子的体积是否发生变化?
转换前后沙子的体积不变,所以铺成的公路路面的体积等于圆锥形沙堆的体积。
3、如图,测量中经常使用铅锤。这个铅锤的体积是
多少立方厘米?
≈26.17(cm3)
小结
圆锥的体积=底面积×高× ,
用字母表示为V= Sh。
谢谢大家的聆听!
3.2.2圆锥的体积
1、引导学生通过观看实验,推导出圆锥体积的计算公式;并能运用计算公式求圆锥的体积。
2、培养 学生的观察、操作、分析表达,归纳概括能力。
3、培养学生良好的学习兴趣。
教学目标
V=abc
V=a3
一、复习旧知
圆柱公式复习
V柱=πr2h
圆柱
圆锥
准备等底等高的圆柱形容器和圆锥形容器各一个。
将圆锥形容器装满小米,再倒入圆柱形容器,看几次能倒满。
圆柱的体积等于和它等底等高的圆锥的体积的3倍。
如图进行探索,你有什么发现?
二、新知讲解
我们已经会计算圆柱的体积,如何计算圆锥的体积呢?
圆锥的体积和圆柱的体积有没有关系呢?
圆柱的底面是圆,圆锥的底面也是圆……
圆锥的体积=底面积×高× ,
用字母表示为V= Sh。
有一堆小米,近似于圆锥形,量得
底面周长是9.31厘米,高4厘米。
求它的体积?
1、计算下面各圆锥的体积。
三、小刀试牛
2、如图,测量中经常使用铅锤。这个铅锤的体积是
多少立方厘米?
≈26.17(cm3)
3、一个用钢铸造成的圆锥形铅锤,底面直径是4cm,
高5cm。每立方厘米钢大约重7.8g。这个铅锤重
多少克?(得数保留整数)
3
1
(2)铅锤的体积:
(1)铅锤底面积:
21×7.8≈164(g)
(3)铅锤的质量:
答:这个铅锤大约重164g。
×12.56×5≈21(cm3)
3.14×( )=3.14×4=12.56(cm2)
2
4
2
(1)一个圆柱的体积是75.36m3,与它等底等高的圆锥的体积是( )m3。
25.12
(2)一个圆锥的体积是141.3m3,与它等底等高的圆柱的体积是( )m3。
423.9
141.3×3=423.9(m3)
四、课堂练习
75.36× =25.12(m3)
3
1
1、填空题
2、 一个圆锥形沙堆,底面积是28.26m2,高是2.5m。用这堆
沙在10m宽的公路上铺2cm厚的路面,能铺多少米?
2cm=0.02m
(1)沙堆的体积:
=9.42×2.5
=23.55(m3)
23.55÷10÷0.02
=2.355÷0.02
=117.75(m)
(2)所铺公路的长度
答:能铺117.75m。
×28.26×2.5
3
1
请你想一想,转换前后沙子的体积是否发生变化?
转换前后沙子的体积不变,所以铺成的公路路面的体积等于圆锥形沙堆的体积。
3、如图,测量中经常使用铅锤。这个铅锤的体积是
多少立方厘米?
≈26.17(cm3)
小结
圆锥的体积=底面积×高× ,
用字母表示为V= Sh。
谢谢大家的聆听!
