山东临清2012-2013学年九年级上数学期中考试试题(含答案)
文档属性
| 名称 | 山东临清2012-2013学年九年级上数学期中考试试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 183.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-06 07:12:15 | ||
图片预览




文档简介
2012~2013学年第一学期九年级数学期中检测
(考试时间120分钟,满分120分)
选择题(本题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项符合题目要求,请把正确选项的序号填在答题卷的相应位置)
1.观察下列银行标志,从图案看既是轴对称图形又是中心对称图形的有( )个
A.1个 B.2个 C.3个 D.4个
2.在平面直角坐标系中,将点P(-2,3)沿x轴方向向右平移3个单位,再向下平移2个单位得到点Q,则点Q的坐标是( )
A.(-4,6) B.(-2,5) C.(-5,6) D.(1,1)
3.如果关于x的一元二次方程x2+px+q=0的两根分别为,,那么p、q的值分别是( )
A.-3,2 B.3,-2 C.2,-3 D.2,3
4.顺次连接矩形四边中点所得的四边形一定是( )
A.正方形 B.矩形 C.菱形 D.平行四边形
5.如图,在平面直角坐标系中,菱形OABC的顶点C坐标是(3,4)则顶点A、B的坐标分别是( )
A.(4,0)(7,4) B.(4,0)(8,4)
C.(5,0)(7,4) D.(5,0)(8,4)
6.如图,在△ABC中,D,E分别是边AC,AB的中点,连接BD.若BD平分∠ABC,则下列结论错误的是 ( )
A.BC=2BE B.∠A=∠EDA
C.BC=2AD D.BD⊥AC
7.如图,四边形ABCD是平行四边形,点E在边BC上,如果点F是边AD上的点,那么△CDF与△ABE不一定全等的条件是( )
A.
DF=BE
B.
AF=CE
C.
CF=AE
D.
CF∥AE
8.某市2009年平均房价为每平方米4000元.连续两年增长后,2011年平均房价达到每平方米5500元,设这两年平均房价年平均增长率为x,根据题意,下面所列方程正确的是( )
A.5500(1+x)2=4000 B.5500(1﹣x)2=4000
C.4000(1﹣x)2=5500 D.4000(1+x)2=5500
9.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长( )
A.4 B.6 C.8 D.10
10.边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB′C′D′,C′B′与CD交于点H,则DH的长为( )
A. B. C.1 D.2
11.如图,菱形ABCD的周长为20,DE⊥AB,垂足为E,,则下列结论:① ;② ; ③菱形的面积为 ; ④。
其正确的个数( )
A. 1 B.2 C.3 D.4
12.如图,在△ABC中,点E,D,F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.下列四个判断中,不正确的是( )
A.四边形AEDF是平行四边形
B.如果∠BAC=90°,那么四边形AEDF是矩形.
C. 如果AD平分∠BAC,那么四边形AEDF是菱形.
D. 如果AD⊥BC且AB=AC,那么四边形AEDF是正方形.
二、填空题(本题共5个小题,每题3分,共15分。直接将最后答案填在答卷的相应位置)
13.等腰三角形的底和腰是方程的两根,则这个三角形的周长为 .
14.如图,四边形ABCD是平行四边形,AC、BD交于点O,∠1=∠2,∠BOC=120°,AB=4,则四边形ABCD的面积= .
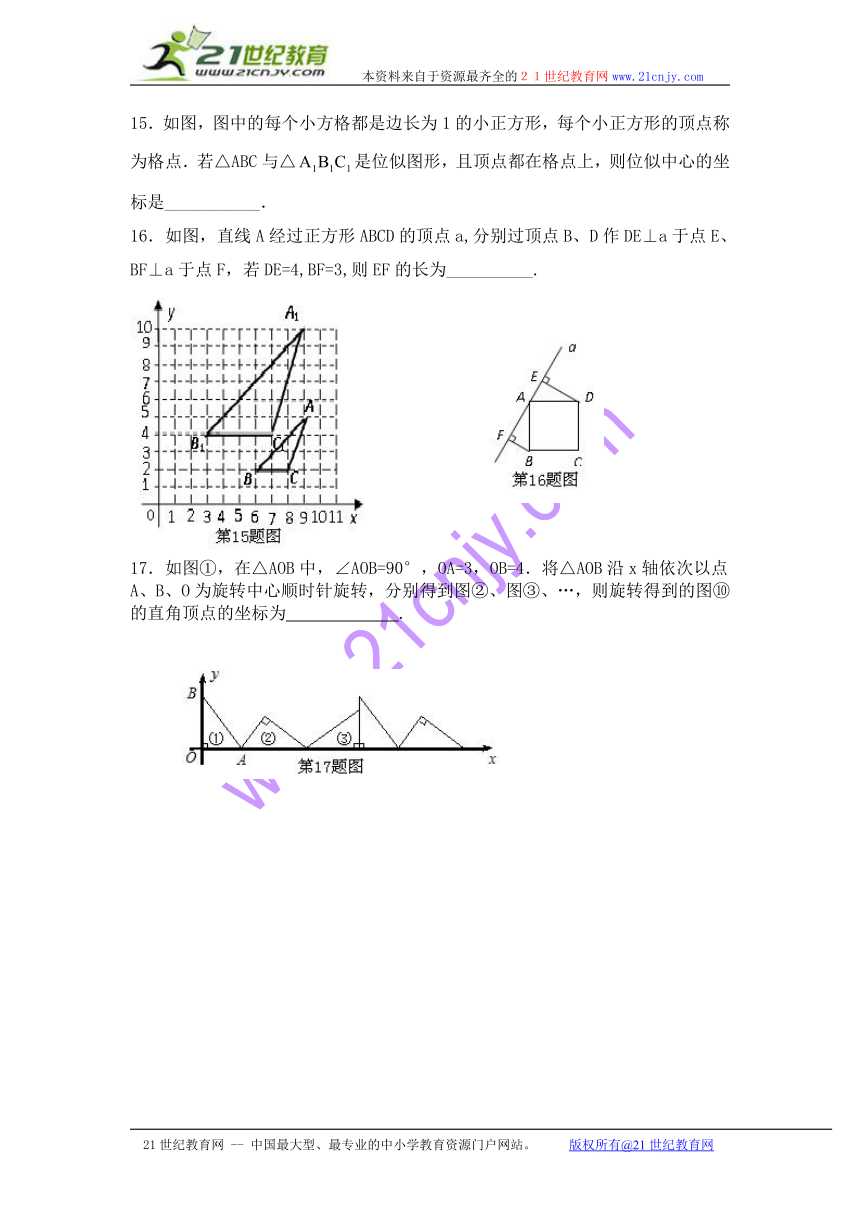
15.如图,图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若△ABC与△是位似图形,且顶点都在格点上,则位似中心的坐标是___________.
16.如图,直线A经过正方形ABCD的顶点a,分别过顶点B、D作DE⊥a于点E、BF⊥a于点F,若DE=4,BF=3,则EF的长为__________.
17.如图①,在△AOB中,∠AOB=90°,OA=3,OB=4.将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑩的直角顶点的坐标为 .
2011~2013学年度第一学期九年级数学期中检测答卷
(考试时间120分钟,满分120分)
题号
一
二
三
总分
18
19
20
21
22
23
24
25
得分
一、选择题:(本题共12个小题,每题3分,共36分,在每小题给出的四个选项中,只有一项是符合题目要求的)
题号
1
2
3
4
5
6
7
8
9
10
11
12
二、填空题:直接将最后答案填在答卷的相应位置(本题共5个小题,每题3分,共15分)
13. ;14. ; 15. ;
16. ;17. 。
三、解答题(本题共8个小题,共69分,解答应写出必要的文字说明、计算过程或推演步骤)
18.(本题满分12分)解方程。
(1); (2)。
19.(本题满分7分)如图,在□ABCD中,已知点E在AB上,点F在CD上,且.
(1)求证:;
(2)连结BD,并写出图中所有的全等三角形.(不要求证明)
20.(本题满分7分)如果关于x的一元二次方程有两个不相等的实数根,
(1)求k的取值范围?
(2)若方程的一根为1,求k的值及方程的另一根
21.(本题满分8分)如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:BD=EC;
(2)若∠E=60°,求∠BAO的度数.
22.(本题满分7分)如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,
(1)求道路的宽; (部分参考数据:322=1024,522=2704,482=2304)
(2)为了使草坪更美观,有人建议把道路进行如图所示修筑方案,试用学过的知识说明,不改变道路的宽,能否满足上面的要求?
23.(本题满分8分)已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.
(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形?并说明理由.
24.(本题满分8分)山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
25.(本题满分12分)将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
(1)如图①,对△ABC作变换[60°,]得△AB′C′,则S△AB′C′:S△ABC= ;若直线BC的延长线与AB′交于点N,与B′C′交于点M,直线BC与直线B′C′所夹的锐角∠B′MN为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
2011~2013学年度第一学期九年级数学期中检测参考答案
(考试时间120分钟,满分120分)
一、选择题(本题共12个小题,每题3分,共36分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
B
D
A
C
D
C
C
D
C
A
C
D
二、填空题(本题共5个小题,每题3分,共15分)
13.10; 14. ; 15.(9,0) ;16.7 ;17.(36,4)。
三、解答题:(本题共8个小题,共69分)
18.(本题满分12分)(1)0、 (2)1、
19.(本题满分7分)(1)在□ABCD中,AB//CD,AB=CD.
∴BE//DF.
∵AE=CF,
∴BE=DF.
∴四边形BFDE是平行四边形.
∴.……4分
(2)连结BD,如图,
图中有三对全等三角形:
△ADE≌△CBF,△BDE≌△DBF,△ABD≌△CDB.……7分
20.(本题满分7分)(1)△=36—4k×9=36—36k>0,k<1,
关于x的一元二次方程,k≠0,
所以k<1且k≠0. ……5分
(2)k=-3.另一根为-3。……7分
21.(本题满分8分)(1)证明:∵菱形ABCD,
∴AB=CD,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD是平行四边形,
∴BD=EC。……4分
(2)解:∵平行四边形BECD,
∴BD∥CE,
∴∠ABO=∠E=60°,
又∵菱形ABCD,
∴AC丄BD,
∠BAO=90°-∠ABO=30°.……8分
22.(本题满分7分)
(1)解:设道路宽x米,根据题意得
解之得:>20(不符合题意舍去)
答:道路宽2米. ……5分
(2)能,运用平移知识,可以将图形转化为上面图形. ……7分
23.(本题满分8分)
(1)证明: ∵四边形ABCD是正方形
∴BC=DC,∠BCD=90°
∴∠DCE=90°
∵CE=CG
∴△BCG≌△DCE. ……4分
(2)四边形BGDE′是平行四边形
∵△DCE绕点D顺时针旋转90°得到△DAE′
∴DE=D E′,CE=AE′
∵△BCG≌△DCE
∴CG=CE,DE=BG
∴D E′= BG,CG= AE′
∵四边形ABCD是正方形
∴AB=CD
∵BE′=GD
又∵D E′= BG
∴四边形BGDE′是平行四边形. ……8分
24.(本题满分8分)
解:(1)设每千克核桃应降价x元。根据题意得,
(60﹣x﹣40)(100+×20)=2240.
化简,得 x2﹣10x+24=0 解得x1=4,x2=6.
答:每千克核桃应降价4元或6元。……4分
(2)由(1)可知每千克核桃可降价4元或6元.
因为要尽可能让利于顾客,所以每千克核桃应降价6元.
此时,售价为:60﹣6=54(元),.
答:该店应按原售价的九折出售.……8分
25.(本题满分12分)
解:(1)答案为:3,60;……4分
根据题意得:△ABC∽△AB′C′,
∴S△AB′C′:S△ABC=()2=()2=3,∠B=∠B′,
∵∠ANB=∠B′NM,
∴∠B′MN=∠BAB′=60°;
(2)∵四边形 ABB′C′是矩形,
∴∠BAC′=90°.
∴θ=∠CAC′=∠BAC′-∠BAC=90°﹣30°=60°.
在 Rt△ABB' 中,∠ABB'=90°,∠BAB′=60°,
∴∠AB′B=30°,
∴n==2;……8分
(3)AB=AC,∠BAC=36°
∴∠ABC=∠ACB=72°
∵四边形ABB′C′是平行四边形,21世纪教育网
∴AC′∥BB′,
∴θ=∠CAC′=∠ACB=72°
∴∠C′AB′=∠BAC=36°,
∵AC′∥BB′
∴∠AB′B=36°
而∠B=∠B,
∴△ABC∽△B′BA,
∴AB:BB′=CB:AB,
∴AB2=CB?BB′=CB(BC+CB′),
∵∠CAC′=72°,∠C′AB′=36°
∴∠AB′C==36°
∴CB′=AC=AB=B′C′
∵BC=1,
∴AB2=1(1+AB),
∴AB=,
∵AB>0,
∴n==.……12分
(考试时间120分钟,满分120分)
选择题(本题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项符合题目要求,请把正确选项的序号填在答题卷的相应位置)
1.观察下列银行标志,从图案看既是轴对称图形又是中心对称图形的有( )个
A.1个 B.2个 C.3个 D.4个
2.在平面直角坐标系中,将点P(-2,3)沿x轴方向向右平移3个单位,再向下平移2个单位得到点Q,则点Q的坐标是( )
A.(-4,6) B.(-2,5) C.(-5,6) D.(1,1)
3.如果关于x的一元二次方程x2+px+q=0的两根分别为,,那么p、q的值分别是( )
A.-3,2 B.3,-2 C.2,-3 D.2,3
4.顺次连接矩形四边中点所得的四边形一定是( )
A.正方形 B.矩形 C.菱形 D.平行四边形
5.如图,在平面直角坐标系中,菱形OABC的顶点C坐标是(3,4)则顶点A、B的坐标分别是( )
A.(4,0)(7,4) B.(4,0)(8,4)
C.(5,0)(7,4) D.(5,0)(8,4)
6.如图,在△ABC中,D,E分别是边AC,AB的中点,连接BD.若BD平分∠ABC,则下列结论错误的是 ( )
A.BC=2BE B.∠A=∠EDA
C.BC=2AD D.BD⊥AC
7.如图,四边形ABCD是平行四边形,点E在边BC上,如果点F是边AD上的点,那么△CDF与△ABE不一定全等的条件是( )
A.
DF=BE
B.
AF=CE
C.
CF=AE
D.
CF∥AE
8.某市2009年平均房价为每平方米4000元.连续两年增长后,2011年平均房价达到每平方米5500元,设这两年平均房价年平均增长率为x,根据题意,下面所列方程正确的是( )
A.5500(1+x)2=4000 B.5500(1﹣x)2=4000
C.4000(1﹣x)2=5500 D.4000(1+x)2=5500
9.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长( )
A.4 B.6 C.8 D.10
10.边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB′C′D′,C′B′与CD交于点H,则DH的长为( )
A. B. C.1 D.2
11.如图,菱形ABCD的周长为20,DE⊥AB,垂足为E,,则下列结论:① ;② ; ③菱形的面积为 ; ④。
其正确的个数( )
A. 1 B.2 C.3 D.4
12.如图,在△ABC中,点E,D,F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.下列四个判断中,不正确的是( )
A.四边形AEDF是平行四边形
B.如果∠BAC=90°,那么四边形AEDF是矩形.
C. 如果AD平分∠BAC,那么四边形AEDF是菱形.
D. 如果AD⊥BC且AB=AC,那么四边形AEDF是正方形.
二、填空题(本题共5个小题,每题3分,共15分。直接将最后答案填在答卷的相应位置)
13.等腰三角形的底和腰是方程的两根,则这个三角形的周长为 .
14.如图,四边形ABCD是平行四边形,AC、BD交于点O,∠1=∠2,∠BOC=120°,AB=4,则四边形ABCD的面积= .
15.如图,图中的每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若△ABC与△是位似图形,且顶点都在格点上,则位似中心的坐标是___________.
16.如图,直线A经过正方形ABCD的顶点a,分别过顶点B、D作DE⊥a于点E、BF⊥a于点F,若DE=4,BF=3,则EF的长为__________.
17.如图①,在△AOB中,∠AOB=90°,OA=3,OB=4.将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑩的直角顶点的坐标为 .
2011~2013学年度第一学期九年级数学期中检测答卷
(考试时间120分钟,满分120分)
题号
一
二
三
总分
18
19
20
21
22
23
24
25
得分
一、选择题:(本题共12个小题,每题3分,共36分,在每小题给出的四个选项中,只有一项是符合题目要求的)
题号
1
2
3
4
5
6
7
8
9
10
11
12
二、填空题:直接将最后答案填在答卷的相应位置(本题共5个小题,每题3分,共15分)
13. ;14. ; 15. ;
16. ;17. 。
三、解答题(本题共8个小题,共69分,解答应写出必要的文字说明、计算过程或推演步骤)
18.(本题满分12分)解方程。
(1); (2)。
19.(本题满分7分)如图,在□ABCD中,已知点E在AB上,点F在CD上,且.
(1)求证:;
(2)连结BD,并写出图中所有的全等三角形.(不要求证明)
20.(本题满分7分)如果关于x的一元二次方程有两个不相等的实数根,
(1)求k的取值范围?
(2)若方程的一根为1,求k的值及方程的另一根
21.(本题满分8分)如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:BD=EC;
(2)若∠E=60°,求∠BAO的度数.
22.(本题满分7分)如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,
(1)求道路的宽; (部分参考数据:322=1024,522=2704,482=2304)
(2)为了使草坪更美观,有人建议把道路进行如图所示修筑方案,试用学过的知识说明,不改变道路的宽,能否满足上面的要求?
23.(本题满分8分)已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.
(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形?并说明理由.
24.(本题满分8分)山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
25.(本题满分12分)将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
(1)如图①,对△ABC作变换[60°,]得△AB′C′,则S△AB′C′:S△ABC= ;若直线BC的延长线与AB′交于点N,与B′C′交于点M,直线BC与直线B′C′所夹的锐角∠B′MN为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
2011~2013学年度第一学期九年级数学期中检测参考答案
(考试时间120分钟,满分120分)
一、选择题(本题共12个小题,每题3分,共36分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
B
D
A
C
D
C
C
D
C
A
C
D
二、填空题(本题共5个小题,每题3分,共15分)
13.10; 14. ; 15.(9,0) ;16.7 ;17.(36,4)。
三、解答题:(本题共8个小题,共69分)
18.(本题满分12分)(1)0、 (2)1、
19.(本题满分7分)(1)在□ABCD中,AB//CD,AB=CD.
∴BE//DF.
∵AE=CF,
∴BE=DF.
∴四边形BFDE是平行四边形.
∴.……4分
(2)连结BD,如图,
图中有三对全等三角形:
△ADE≌△CBF,△BDE≌△DBF,△ABD≌△CDB.……7分
20.(本题满分7分)(1)△=36—4k×9=36—36k>0,k<1,
关于x的一元二次方程,k≠0,
所以k<1且k≠0. ……5分
(2)k=-3.另一根为-3。……7分
21.(本题满分8分)(1)证明:∵菱形ABCD,
∴AB=CD,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD是平行四边形,
∴BD=EC。……4分
(2)解:∵平行四边形BECD,
∴BD∥CE,
∴∠ABO=∠E=60°,
又∵菱形ABCD,
∴AC丄BD,
∠BAO=90°-∠ABO=30°.……8分
22.(本题满分7分)
(1)解:设道路宽x米,根据题意得
解之得:>20(不符合题意舍去)
答:道路宽2米. ……5分
(2)能,运用平移知识,可以将图形转化为上面图形. ……7分
23.(本题满分8分)
(1)证明: ∵四边形ABCD是正方形
∴BC=DC,∠BCD=90°
∴∠DCE=90°
∵CE=CG
∴△BCG≌△DCE. ……4分
(2)四边形BGDE′是平行四边形
∵△DCE绕点D顺时针旋转90°得到△DAE′
∴DE=D E′,CE=AE′
∵△BCG≌△DCE
∴CG=CE,DE=BG
∴D E′= BG,CG= AE′
∵四边形ABCD是正方形
∴AB=CD
∵BE′=GD
又∵D E′= BG
∴四边形BGDE′是平行四边形. ……8分
24.(本题满分8分)
解:(1)设每千克核桃应降价x元。根据题意得,
(60﹣x﹣40)(100+×20)=2240.
化简,得 x2﹣10x+24=0 解得x1=4,x2=6.
答:每千克核桃应降价4元或6元。……4分
(2)由(1)可知每千克核桃可降价4元或6元.
因为要尽可能让利于顾客,所以每千克核桃应降价6元.
此时,售价为:60﹣6=54(元),.
答:该店应按原售价的九折出售.……8分
25.(本题满分12分)
解:(1)答案为:3,60;……4分
根据题意得:△ABC∽△AB′C′,
∴S△AB′C′:S△ABC=()2=()2=3,∠B=∠B′,
∵∠ANB=∠B′NM,
∴∠B′MN=∠BAB′=60°;
(2)∵四边形 ABB′C′是矩形,
∴∠BAC′=90°.
∴θ=∠CAC′=∠BAC′-∠BAC=90°﹣30°=60°.
在 Rt△ABB' 中,∠ABB'=90°,∠BAB′=60°,
∴∠AB′B=30°,
∴n==2;……8分
(3)AB=AC,∠BAC=36°
∴∠ABC=∠ACB=72°
∵四边形ABB′C′是平行四边形,21世纪教育网
∴AC′∥BB′,
∴θ=∠CAC′=∠ACB=72°
∴∠C′AB′=∠BAC=36°,
∵AC′∥BB′
∴∠AB′B=36°
而∠B=∠B,
∴△ABC∽△B′BA,
∴AB:BB′=CB:AB,
∴AB2=CB?BB′=CB(BC+CB′),
∵∠CAC′=72°,∠C′AB′=36°
∴∠AB′C==36°
∴CB′=AC=AB=B′C′
∵BC=1,
∴AB2=1(1+AB),
∴AB=,
∵AB>0,
∴n==.……12分
同课章节目录
