第一轮复习课件 功
图片预览





文档简介
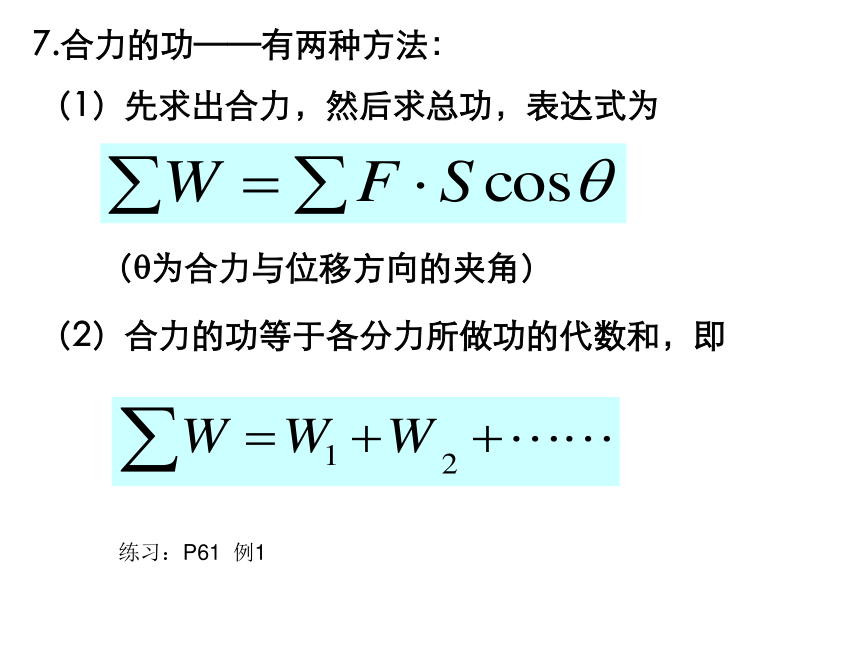
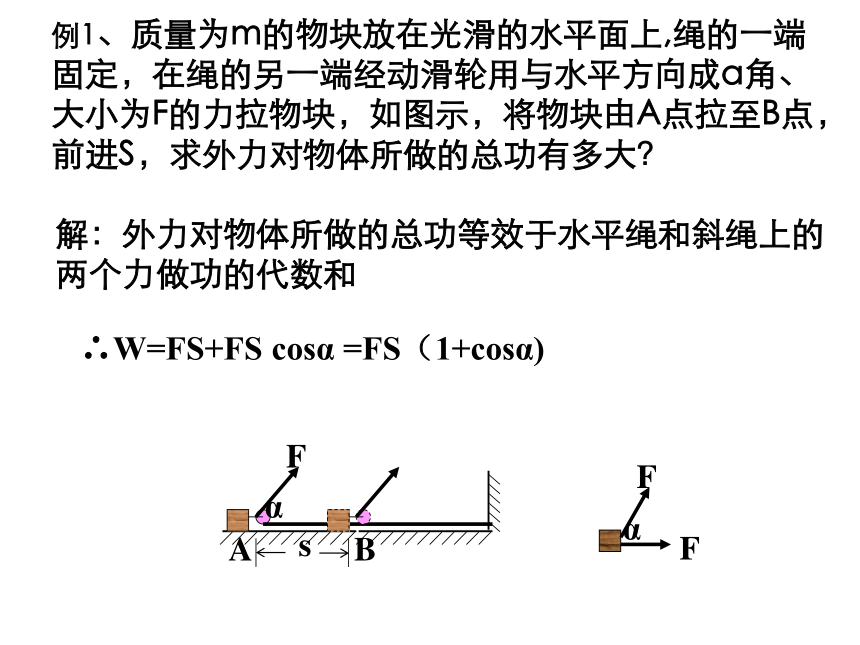
课件28张PPT。功考点一、功的概念1.定义:物体受到力的作用,并在力方向上发生一段位移,就说力对物体做了功.2.公式:W=Fscosα,其中α为F与s的夹角,F是力的大小,s一般是物体相对地面的位移,而不是相对于和它接触的物体的位移.3.应用中的注意点①公式只适用于恒力做功② F和S是对应同一个物体的;③恒力做功多少只与F、S及二者夹角余弦有关,而与物体的加速度大小、速度大小、运动时间长短等都无关,即与物体的运动性质无关,同时与有无其它力做功也无关。4.物理意义:功是能量转化的量度.5.单位:焦耳(J) 1J=1N·m.6.功是标量,没有方向、但是有正负,正负表示能量转化的方向.表示物体是输入了能量还是输出了能量 .①当0≤α<90°时W>0,力对物体做正功;若物体做直线运动,由力和位移夹角来判断较方便。②当α=90时W=0,力对物体不做功;③当90°<α≤180°时,W<0,力对物体做负功或说成物体克服这个力做功.若物体做曲线运动,利用力和速度的夹角来判断做。① 0≤α<90O时,力对物体做正功;② α=90O时,力对物体不做功。③ 90O<α≤180O时,力对物体做负功(或物体克服力做功)。7.合力的功——有两种方法:(1)先求出合力,然后求总功,表达式为(?为合力与位移方向的夹角)(2)合力的功等于各分力所做功的代数和,即练习:P61 例1例1、质量为m的物块放在光滑的水平面上,绳的一端固定,在绳的另一端经动滑轮用与水平方向成α角、大小为F的力拉物块,如图示,将物块由A点拉至B点,前进S,求外力对物体所做的总功有多大?解:外力对物体所做的总功等效于水平绳和斜绳上的两个力做功的代数和∴W=FS+FS cosα =FS(1+cosα)用总功等于各力做功的代数和求之C真题1(上海)如图所示,质量为m的物块始终固定在倾角为α的斜面上,下面说法中正确的是 ( ) A.若斜面向左匀速移动距离s,斜面对物块没有做功
B.若斜面向上匀速移动距离s,斜面对物块做功mgs
C.若斜面向左以加速度a移动距离s,斜面对物块做功mas
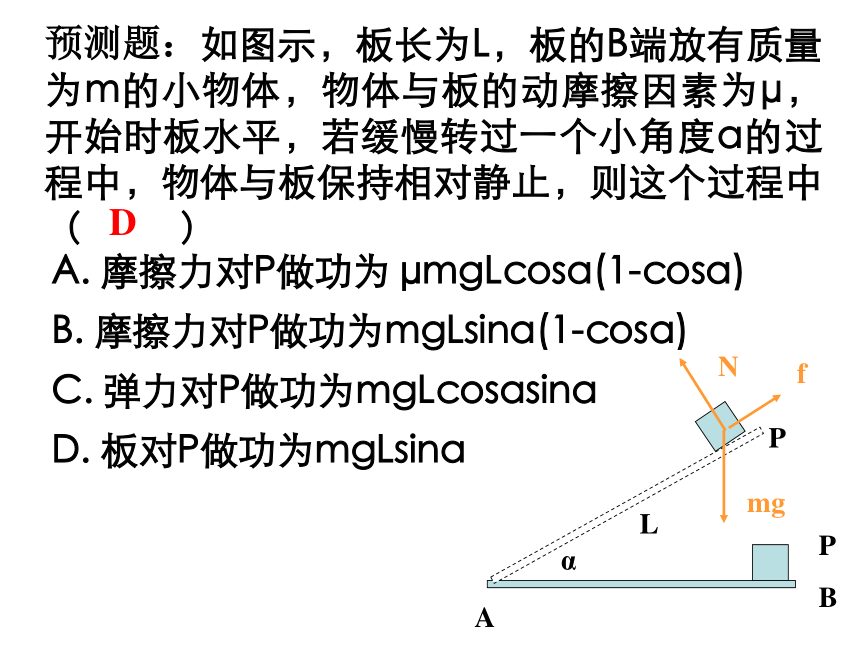
D.若斜面向下以加速度a移动距离s,斜面对物块做功m(g+a)sα预测题:如图示,板长为L,板的B端放有质量为m的小物体,物体与板的动摩擦因素为μ,开始时板水平,若缓慢转过一个小角度α的过程中,物体与板保持相对静止,则这个过程中( )A. 摩擦力对P做功为 μmgLcosα(1-cosα)
B. 摩擦力对P做功为mgLsinα(1-cosα)
C. 弹力对P做功为mgLcosαsinα
D. 板对P做功为mgLsinαD8.功和冲量的比较(1)功和冲量都是过程量,功表示力在空间上的积累效果,冲量表示力在时间上的积累效果.(2)功是标量,其正、负表示是动力对物体做功还是物体克服阻力做功.冲量是矢量,其正、负号表示方向,计算冲量时要先规定正方向.(3)做功的多少由力的大小、位移的大小及力和位移的夹角三个因素决定.冲量的大小只由力的大小和时间两个因素决定.力作用在物体上一段时间,力的冲量不为零,但力对物体做的功可能为零.考点二.变力做功对于变力做功不能依定义式直接求解,但可依物理规律通过技巧的转化间接求解。1.可用(微元法)无限分小法来求, 过程无限分小后, 可认为每小段是恒力做功。 例、一辆马车在力F=100N的作用下绕半径为50m的圆形轨道做匀速圆周运动,当车运动一周回到原位置时,车子克服阻力所做的功为多少?2.平均力法: 若变力大小随位移是线性变化,且方向不变时,可将变力的平均值求出后用公式计算。如弹簧的弹力做功就可以用此法计算。3.利用F-S图像,F-S图线与坐标轴所包围的面积即是力F做功的数值。例.用铁锤将一铁钉击入木块,设木块对铁钉的阻力与铁钉进入木块内的深度成正比.在铁锤击第一次时,能把铁钉击入木块内1cm,问击第二次时,能击入多少深度 ? (设铁锤每次做功相等)△x=x2-x1=0.41cm.?4.已知变力做功的平均功率P,则功W=Pt。5.用动能定理进行求解: 由动能定理W=ΔEK可知,将变力的功转换为物体动能的变化量,可将问题轻易解决。
6.用功能关系进行求解。 例: 人在A点拉着细绳通过一定滑轮吊起质量m=50kg的物体,如图,开始绳与水平方向夹角为60度,当人匀速提起重物由A点沿水平方向运动s=2m而到达B点,绳与水平方向成30度,求人对绳的拉力做了多少功?考点三、各种力做功的特点一、重力做功特点(1)重点做功与路径无关,只与物体的始末位置高度差有关?(2)重力做功的大小:W=mg·h(3)重力做功与重力势能的关系:WG=-△Ep=E p1-Ep2 此外,做功多少与路径无关的力还有:匀强电场中的电场力做功,液体的浮力做功等.例、两个底面积都是S的圆桶,放在同一水平面上,桶内装水,水的密度为ρ,两桶间有一细管连通,细管上装有阀门,阀门关闭时,两只桶内水面高度差为h,如图所示.现在把阀门打开,最后两桶水面高度相等,则在此过程中,重力做的
功为 . 二.摩擦力做功的特点:1.静摩擦力做功的特点(1)静摩擦力可以做正功,也可以做负功,还可以不做功。(2)在静摩擦力做功的过程中,只有机械能的相互转移(静摩擦力起着传递机械能的作用),而没有机械能转化为其他形式的能.
(3)相互摩擦的系统内,一对静摩擦力所做功的代数和总为零。1.AB两物体叠放在光滑的水平面上,保持相对静止一起向右做匀加速运动移动S, 则摩擦力f1对A做————功,f2对B做————功。W1=f S W2= - f S W1 + W2= 0正负举例说明:2.小木块置于旋转的水平转台上,随转台一起匀速转动,小木块受到的摩擦力对木块做————功。0若小木块随转台一起加速转动而没有相对滑动,则小木块受到的摩擦力对木块做————功。正3.AB两物体叠放在光滑水平面上,A物体用线系在墙上,B 物体在力 F作用下向右运动,则f1对A做————功,f2对B做————功。 0负4.正在运动的水平传送带上轻轻放一个小木块,小木块受到的摩擦力对小木块做———— 功。开始物体在摩擦力的作用下做匀加速运
动,摩擦力对物体做正功。达到速度v后,物体不受摩擦力,做匀速
运动,不做功.5.AB两物体叠放在光滑水平面上,A物体在力 F作用下在B物体上相对滑动,
则f1对A做————功,f2对B做————功。W1= - fS1W2= fS2W1 + W2= f(S2 - S1 )= - f Δ S负正2.滑动摩擦力做功的特点:(1)滑动摩擦力可以对物体做正功,也可以对物体做负功,当然也可以不做功。(2)一对滑动摩擦力做功的过程中,能量的转化有两个方面:一是相互摩擦的物体之间机械能的转移;二是机械能转化为内能。(3)一对滑动摩擦力的总功等于 - fΔS式中ΔS指物体间的相对位移 (4)转化为内能的量值等于滑动摩擦力与相对位移的乘积,即W=Q(即摩擦生热).
(5)滑动摩擦力、空气摩擦阻力等,在曲线运动或往返运动时等于力和路程(不是位移)的乘积 例.质量为M的长板放在光滑水平面上,一个质量为m的滑块以速度v沿木板表面从A点滑到B点,在木板上前进了L,而木板在水平面上前进了s,如图,设滑块与木板间的动摩擦因数为?求:(1)摩擦力对滑块做的功;
(2)摩擦力对木板做的功;
(3)摩擦力做的总功;
(4)上述过程中机械能转化为内能的大小.【解题回顾】摩擦力是阻力(对滑块)时,它所做的功是负功;摩擦力是动力(对木板)时,它所做的功是正功。我们还体会到摩擦力f和f′虽然是一对作用力和反作用力,但它们做的功却不一定相等.3.一对相互作用力做功特点: 一对相互作用力可以同时做正功,也可以同时做负功,
也可以作用力做正功,反作用力做负功,也可以作用
力做正功, 反作用力不做功,也可以作用力做负功,
反作用力不做功, 不要以为作用力与反作用力大小相等、方向相反,就一定有作用力、反作用力的功数值相等,一正一负.所以作用力与反作用力做功不一定相等,但冲量的大小相等. 练习.下列说法正确的是: ( )
(A)一对摩擦力做的总功,有可能是一负值,有可能
是零;
(B)物体在合外力作用下做变速运动,动能一定变化;
(C)当作用力作正功时,反作用力一定做负功;
(D)当作用力不作功时,反作用力一定也不作功;
(E)合外力对物体做功等于零,物体一定是做匀速直
线运动.A4.弹力做功的特点:弹力对物体可以做正功,可以不做功, 也可以做负功。 【例】如图所示,把A、B两球由图示位置同时由静止释放(绳开始时拉直),则在两球向左下摆动时.下列说法正确的是
A.绳子OA对A球做正功
B.绳子AB对B球不做功
C.绳子AB对A球做负功
D.绳子AB对B球做正功C、D
B.若斜面向上匀速移动距离s,斜面对物块做功mgs
C.若斜面向左以加速度a移动距离s,斜面对物块做功mas
D.若斜面向下以加速度a移动距离s,斜面对物块做功m(g+a)sα预测题:如图示,板长为L,板的B端放有质量为m的小物体,物体与板的动摩擦因素为μ,开始时板水平,若缓慢转过一个小角度α的过程中,物体与板保持相对静止,则这个过程中( )A. 摩擦力对P做功为 μmgLcosα(1-cosα)
B. 摩擦力对P做功为mgLsinα(1-cosα)
C. 弹力对P做功为mgLcosαsinα
D. 板对P做功为mgLsinαD8.功和冲量的比较(1)功和冲量都是过程量,功表示力在空间上的积累效果,冲量表示力在时间上的积累效果.(2)功是标量,其正、负表示是动力对物体做功还是物体克服阻力做功.冲量是矢量,其正、负号表示方向,计算冲量时要先规定正方向.(3)做功的多少由力的大小、位移的大小及力和位移的夹角三个因素决定.冲量的大小只由力的大小和时间两个因素决定.力作用在物体上一段时间,力的冲量不为零,但力对物体做的功可能为零.考点二.变力做功对于变力做功不能依定义式直接求解,但可依物理规律通过技巧的转化间接求解。1.可用(微元法)无限分小法来求, 过程无限分小后, 可认为每小段是恒力做功。 例、一辆马车在力F=100N的作用下绕半径为50m的圆形轨道做匀速圆周运动,当车运动一周回到原位置时,车子克服阻力所做的功为多少?2.平均力法: 若变力大小随位移是线性变化,且方向不变时,可将变力的平均值求出后用公式计算。如弹簧的弹力做功就可以用此法计算。3.利用F-S图像,F-S图线与坐标轴所包围的面积即是力F做功的数值。例.用铁锤将一铁钉击入木块,设木块对铁钉的阻力与铁钉进入木块内的深度成正比.在铁锤击第一次时,能把铁钉击入木块内1cm,问击第二次时,能击入多少深度 ? (设铁锤每次做功相等)△x=x2-x1=0.41cm.?4.已知变力做功的平均功率P,则功W=Pt。5.用动能定理进行求解: 由动能定理W=ΔEK可知,将变力的功转换为物体动能的变化量,可将问题轻易解决。
6.用功能关系进行求解。 例: 人在A点拉着细绳通过一定滑轮吊起质量m=50kg的物体,如图,开始绳与水平方向夹角为60度,当人匀速提起重物由A点沿水平方向运动s=2m而到达B点,绳与水平方向成30度,求人对绳的拉力做了多少功?考点三、各种力做功的特点一、重力做功特点(1)重点做功与路径无关,只与物体的始末位置高度差有关?(2)重力做功的大小:W=mg·h(3)重力做功与重力势能的关系:WG=-△Ep=E p1-Ep2 此外,做功多少与路径无关的力还有:匀强电场中的电场力做功,液体的浮力做功等.例、两个底面积都是S的圆桶,放在同一水平面上,桶内装水,水的密度为ρ,两桶间有一细管连通,细管上装有阀门,阀门关闭时,两只桶内水面高度差为h,如图所示.现在把阀门打开,最后两桶水面高度相等,则在此过程中,重力做的
功为 . 二.摩擦力做功的特点:1.静摩擦力做功的特点(1)静摩擦力可以做正功,也可以做负功,还可以不做功。(2)在静摩擦力做功的过程中,只有机械能的相互转移(静摩擦力起着传递机械能的作用),而没有机械能转化为其他形式的能.
(3)相互摩擦的系统内,一对静摩擦力所做功的代数和总为零。1.AB两物体叠放在光滑的水平面上,保持相对静止一起向右做匀加速运动移动S, 则摩擦力f1对A做————功,f2对B做————功。W1=f S W2= - f S W1 + W2= 0正负举例说明:2.小木块置于旋转的水平转台上,随转台一起匀速转动,小木块受到的摩擦力对木块做————功。0若小木块随转台一起加速转动而没有相对滑动,则小木块受到的摩擦力对木块做————功。正3.AB两物体叠放在光滑水平面上,A物体用线系在墙上,B 物体在力 F作用下向右运动,则f1对A做————功,f2对B做————功。 0负4.正在运动的水平传送带上轻轻放一个小木块,小木块受到的摩擦力对小木块做———— 功。开始物体在摩擦力的作用下做匀加速运
动,摩擦力对物体做正功。达到速度v后,物体不受摩擦力,做匀速
运动,不做功.5.AB两物体叠放在光滑水平面上,A物体在力 F作用下在B物体上相对滑动,
则f1对A做————功,f2对B做————功。W1= - fS1W2= fS2W1 + W2= f(S2 - S1 )= - f Δ S负正2.滑动摩擦力做功的特点:(1)滑动摩擦力可以对物体做正功,也可以对物体做负功,当然也可以不做功。(2)一对滑动摩擦力做功的过程中,能量的转化有两个方面:一是相互摩擦的物体之间机械能的转移;二是机械能转化为内能。(3)一对滑动摩擦力的总功等于 - fΔS式中ΔS指物体间的相对位移 (4)转化为内能的量值等于滑动摩擦力与相对位移的乘积,即W=Q(即摩擦生热).
(5)滑动摩擦力、空气摩擦阻力等,在曲线运动或往返运动时等于力和路程(不是位移)的乘积 例.质量为M的长板放在光滑水平面上,一个质量为m的滑块以速度v沿木板表面从A点滑到B点,在木板上前进了L,而木板在水平面上前进了s,如图,设滑块与木板间的动摩擦因数为?求:(1)摩擦力对滑块做的功;
(2)摩擦力对木板做的功;
(3)摩擦力做的总功;
(4)上述过程中机械能转化为内能的大小.【解题回顾】摩擦力是阻力(对滑块)时,它所做的功是负功;摩擦力是动力(对木板)时,它所做的功是正功。我们还体会到摩擦力f和f′虽然是一对作用力和反作用力,但它们做的功却不一定相等.3.一对相互作用力做功特点: 一对相互作用力可以同时做正功,也可以同时做负功,
也可以作用力做正功,反作用力做负功,也可以作用
力做正功, 反作用力不做功,也可以作用力做负功,
反作用力不做功, 不要以为作用力与反作用力大小相等、方向相反,就一定有作用力、反作用力的功数值相等,一正一负.所以作用力与反作用力做功不一定相等,但冲量的大小相等. 练习.下列说法正确的是: ( )
(A)一对摩擦力做的总功,有可能是一负值,有可能
是零;
(B)物体在合外力作用下做变速运动,动能一定变化;
(C)当作用力作正功时,反作用力一定做负功;
(D)当作用力不作功时,反作用力一定也不作功;
(E)合外力对物体做功等于零,物体一定是做匀速直
线运动.A4.弹力做功的特点:弹力对物体可以做正功,可以不做功, 也可以做负功。 【例】如图所示,把A、B两球由图示位置同时由静止释放(绳开始时拉直),则在两球向左下摆动时.下列说法正确的是
A.绳子OA对A球做正功
B.绳子AB对B球不做功
C.绳子AB对A球做负功
D.绳子AB对B球做正功C、D
