2022年人教版八年级数学 下册 19.2.2 一次函数 第2课时 用待定系数法求一次函数的解析式 课件(共42张)
文档属性
| 名称 | 2022年人教版八年级数学 下册 19.2.2 一次函数 第2课时 用待定系数法求一次函数的解析式 课件(共42张) |

|
|
| 格式 | zip | ||
| 文件大小 | 441.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 19:06:18 | ||
图片预览






文档简介
(共29张PPT)
温故知新
1.什么是一次函数?
2.一次函数解析式?
3.一次函数的性质?
你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
思考:
反过来已知一个一次函数的图象经过两个具体的点,
你能求出它的解析式吗?
两点法——两点确定一条直线
导入新课
19.2.2 一次函数
人教版八年级数学 下册
第2课时 用待定系数法求一次函数的解析式
学习目标
1.探究一次函数的概念及其解析式。
2. 能从图象角度理解正比例函数与一次函数的关系。
3.能初步应用一次函数模型解决现实生活中的问题。
画出函数y=x+1,y=-x+1,y=2x+1, y=-2x+1的图象。
解:列表
x 0 1
y=x+1
y=-x+1
y=2x+1
y=-2x+1
1
1
1
0
2
1
3
合作探究
目标导学一:用待定系数法求一次函数解析式
-1
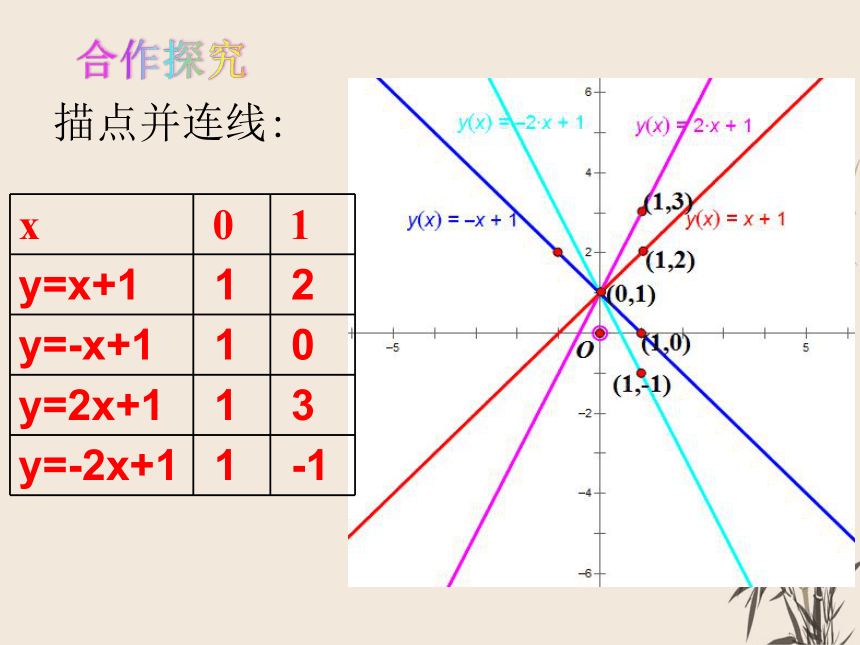
x 0 1
y=x+1 1 2
y=-x+1 1 0
y=2x+1 1 3
y=-2x+1 1 -1
描点并连线:
合作探究
例1 已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式.
分析:一次函数的图象过点(3,5)与(-4,-9),因此这两点的坐标适合一次函数
精典例题
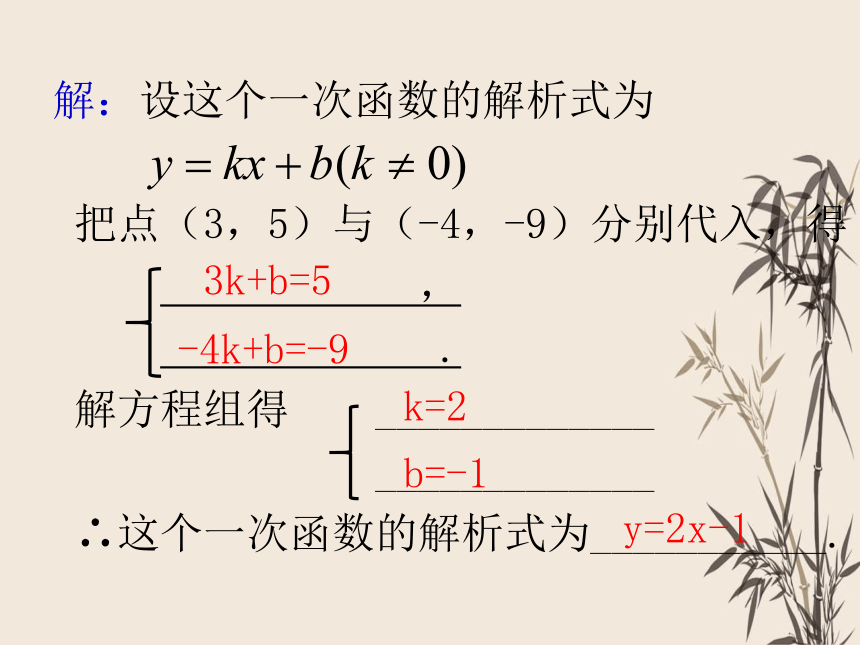
解:设这个一次函数的解析式为
把点(3,5)与(-4,-9)分别代入,得
,
.
解方程组得 _____________
_____________
∴这个一次函数的解析式为___________.
y=2x-1
3k+b=5
-4k+b=-9
k=2
b=-1
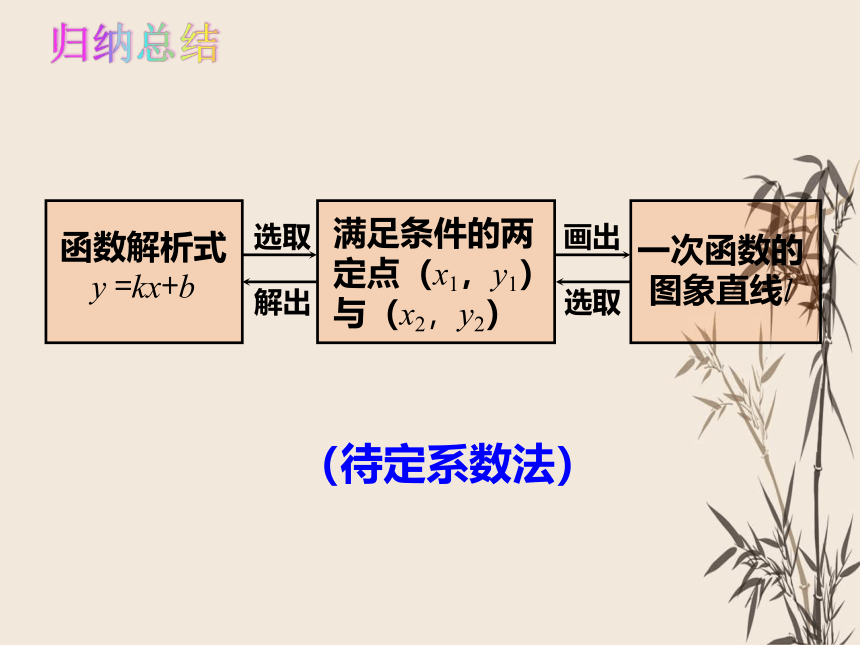
(待定系数法)
满足条件的两 定点(x1,y1)与(x2,y2)
函数解析式
y =kx+b
一次函数的 图象直线l
选取
解出
画出
选取
归纳总结
先设出函数解析式,
再根据条件确定解析式中未知系数,从而得出函数解析式的方法,
叫做待定系数法。
归纳总结
待定系数法:
(1)设:设一次函数的解析式为 ;
(2)代:把图象上的点(x1,y1),(x2,y2)代入一次函
数的解析式,组成_________方程组;
(3)求:求解二元一次方程组得k,b的值;
(4)写(还原):把k,b的值代入一次函数的解析式.
待定系数法求一次函数解析式的步骤:
y=kx+b(k≠0)
二元一次
1.已知一次函数的图象经过点(-4,2)和点(2,3),求这个函数的解析式。
解:设这个一次函数的解析式为y=kx+b(k≠0)
把点(-4,2)与(2,3)分别代入,得
解方程组得
∴这个一次函数的解析式为___________.
即学即练
2.若一次函数的图象经过点 A(2,0)且与直线y=-x+3平行,求其解析式.
解:设这个一次函数的解析式为y=kx+b.
k = -1,
2k + b = 0,
{
由题意得
k = -1,
b = 2.
{
解得
∴y=-x+2.
即学即练
例2 “黄金1号”玉米种子的价格为5元/kg.如果一次购买2kg以上的种子,超过2kg部分的种子价格打8折.
(1)填写下表
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 ...
付款金额/元 ...
目标导学二:一次函数的图象的实际应用
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
(3)一次购买1.5公斤种子,需付款多少元?一次购买3公斤种子,则需付款多少元?
合作探究
分析:从题目可知,付款金额与__________ 有关.若购买种子量为:0≤x≤2时,种子价格y为 ;若购买种子量为x>2时,种子价格y为 __ .
种子价格
5x
4(x-2)+10=4x+2
解:(1)填表
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 ...
付款金额/元 2.5 5 7.5 10 12 14 16 18 ...
合作探究
(2)设购买量为x公斤,付款金额为y元.
当0≤x≤2时,
y= ;
当x>2时,
y= ;
y与x的函数解析式合起来
表示为:y=
函数图象如图:
5x
4(x-2)+10=4x+2
合作探究
(3)一次购买1.5公斤种子需付款 元;
一次购买3公斤种子需付款 元.
7.5
14
合作探究
A城有肥料200吨,B城有肥料300吨,现要把这些肥料全部运往C、D两乡。从A城往C、D两乡运肥料的费用分别为每吨20元和25元;从B城往C、D两乡运肥料的费用分别为每吨15元和24元,现C乡需要肥料240吨, D乡需要肥料260吨,怎样调运总运费最少?
解:设总运费为y元,A城运往C乡的肥料量
为x吨,那么A城运往D乡的肥料量为(200-x)
吨,B城运往C乡的肥料量为(240-x)吨, B城
运往D乡的肥料量为(60+x)吨.
由总运费与各运输量的关系可知,反映
y与x之间关系的函数为
y=20x+25(200-x)+15(240-x)+24(60+x)
y=4x+10040 (0≤x≤200)
化简得:
画y=4x+10040 (0≤x≤200)
列表:
描点:
连线:
x
y=4x
0
1
由解析式和图象可以看出:当x=0时,运费y有最小值10040.
A城→C乡0吨
A城→D乡200吨
B城→C乡240吨
B城→D乡60吨
精典例题
设:设一次函数的解析式为y=kx+b(k≠0);
代:把图象上的点(x1,y1),(x2,y2)代入一次函
数的解析式,组成二元一次方程组;
求:求解二元一次方程组得k,b的值;
写(还原):把k,b的值代入一次函数的解析式.
待定系数法求一次函数解析式的步骤
一次函数与实际问题
课堂总结
1.小明从家步行到校车站台,等候坐校车去学校,图中的折线表示这一过程中小明的路程s( km )与所花时间t( min )间的函数关系.下列说法:①他步行了1 km到校车站台;②他步行的速度是100 m/min;③他在校车站台等了6 min;④校车运行的速度是200 m/min.其中错误的是( )
A.① B.② C.③ D.④
检测目标
D
2.若一次函数y=kx+b的图象经过第一、三、四象限,则 k、b应满足( )
A.k>0,b>0
B.k>0,b<0
C.k<0,b>0
D.k<0,b<0
B
检测目标
3.一次函数y=kx+b的图象如图,则k、b的值分别为( )
(A)k=- ,b=1 (B)k=-2,b=1
(C)k= ,b=1 (D)k=2,b=1
x
y
o
1
1
B
检测目标
4.某航空公司规定,旅客乘机所携带行李的质量x( kg )与其运费y( 元 )由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量( )
A
检测目标
A.20 kg B.25 kg
C.28 kg D.30 kg
5.如图1,甲、乙两个容器内都装了一定数量的水,现将甲容器中的水匀速注入乙容器中.图2中的线段AB,CD分别表示容器中水的深度h(厘米)与注入时间t(分钟)之间的函数图象.下列结论错误的是( )
D
检测目标
A.注水前乙容器内水的高度是5厘米
B.甲容器内的水4分钟全部注入乙容器
C.注水2分钟时,甲、乙两个容器中水的深度相等
D.注水1分钟时,甲容器的水比乙容器的水深5厘米
6.若一直线与另一直线y=-3x+2交于y轴同一点,且过 (2,-6),你能求出这条直线的解析式吗?
答案:y=-4x+2
分析:直线y=-3x+2与y轴的交点为(0,2),于是得知该直线过点(0,2),(2,-6),再用待定系数法求解即可.
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
温故知新
1.什么是一次函数?
2.一次函数解析式?
3.一次函数的性质?
你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
思考:
反过来已知一个一次函数的图象经过两个具体的点,
你能求出它的解析式吗?
两点法——两点确定一条直线
导入新课
19.2.2 一次函数
人教版八年级数学 下册
第2课时 用待定系数法求一次函数的解析式
学习目标
1.探究一次函数的概念及其解析式。
2. 能从图象角度理解正比例函数与一次函数的关系。
3.能初步应用一次函数模型解决现实生活中的问题。
画出函数y=x+1,y=-x+1,y=2x+1, y=-2x+1的图象。
解:列表
x 0 1
y=x+1
y=-x+1
y=2x+1
y=-2x+1
1
1
1
0
2
1
3
合作探究
目标导学一:用待定系数法求一次函数解析式
-1
x 0 1
y=x+1 1 2
y=-x+1 1 0
y=2x+1 1 3
y=-2x+1 1 -1
描点并连线:
合作探究
例1 已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式.
分析:一次函数的图象过点(3,5)与(-4,-9),因此这两点的坐标适合一次函数
精典例题
解:设这个一次函数的解析式为
把点(3,5)与(-4,-9)分别代入,得
,
.
解方程组得 _____________
_____________
∴这个一次函数的解析式为___________.
y=2x-1
3k+b=5
-4k+b=-9
k=2
b=-1
(待定系数法)
满足条件的两 定点(x1,y1)与(x2,y2)
函数解析式
y =kx+b
一次函数的 图象直线l
选取
解出
画出
选取
归纳总结
先设出函数解析式,
再根据条件确定解析式中未知系数,从而得出函数解析式的方法,
叫做待定系数法。
归纳总结
待定系数法:
(1)设:设一次函数的解析式为 ;
(2)代:把图象上的点(x1,y1),(x2,y2)代入一次函
数的解析式,组成_________方程组;
(3)求:求解二元一次方程组得k,b的值;
(4)写(还原):把k,b的值代入一次函数的解析式.
待定系数法求一次函数解析式的步骤:
y=kx+b(k≠0)
二元一次
1.已知一次函数的图象经过点(-4,2)和点(2,3),求这个函数的解析式。
解:设这个一次函数的解析式为y=kx+b(k≠0)
把点(-4,2)与(2,3)分别代入,得
解方程组得
∴这个一次函数的解析式为___________.
即学即练
2.若一次函数的图象经过点 A(2,0)且与直线y=-x+3平行,求其解析式.
解:设这个一次函数的解析式为y=kx+b.
k = -1,
2k + b = 0,
{
由题意得
k = -1,
b = 2.
{
解得
∴y=-x+2.
即学即练
例2 “黄金1号”玉米种子的价格为5元/kg.如果一次购买2kg以上的种子,超过2kg部分的种子价格打8折.
(1)填写下表
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 ...
付款金额/元 ...
目标导学二:一次函数的图象的实际应用
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
(3)一次购买1.5公斤种子,需付款多少元?一次购买3公斤种子,则需付款多少元?
合作探究
分析:从题目可知,付款金额与__________ 有关.若购买种子量为:0≤x≤2时,种子价格y为 ;若购买种子量为x>2时,种子价格y为 __ .
种子价格
5x
4(x-2)+10=4x+2
解:(1)填表
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 ...
付款金额/元 2.5 5 7.5 10 12 14 16 18 ...
合作探究
(2)设购买量为x公斤,付款金额为y元.
当0≤x≤2时,
y= ;
当x>2时,
y= ;
y与x的函数解析式合起来
表示为:y=
函数图象如图:
5x
4(x-2)+10=4x+2
合作探究
(3)一次购买1.5公斤种子需付款 元;
一次购买3公斤种子需付款 元.
7.5
14
合作探究
A城有肥料200吨,B城有肥料300吨,现要把这些肥料全部运往C、D两乡。从A城往C、D两乡运肥料的费用分别为每吨20元和25元;从B城往C、D两乡运肥料的费用分别为每吨15元和24元,现C乡需要肥料240吨, D乡需要肥料260吨,怎样调运总运费最少?
解:设总运费为y元,A城运往C乡的肥料量
为x吨,那么A城运往D乡的肥料量为(200-x)
吨,B城运往C乡的肥料量为(240-x)吨, B城
运往D乡的肥料量为(60+x)吨.
由总运费与各运输量的关系可知,反映
y与x之间关系的函数为
y=20x+25(200-x)+15(240-x)+24(60+x)
y=4x+10040 (0≤x≤200)
化简得:
画y=4x+10040 (0≤x≤200)
列表:
描点:
连线:
x
y=4x
0
1
由解析式和图象可以看出:当x=0时,运费y有最小值10040.
A城→C乡0吨
A城→D乡200吨
B城→C乡240吨
B城→D乡60吨
精典例题
设:设一次函数的解析式为y=kx+b(k≠0);
代:把图象上的点(x1,y1),(x2,y2)代入一次函
数的解析式,组成二元一次方程组;
求:求解二元一次方程组得k,b的值;
写(还原):把k,b的值代入一次函数的解析式.
待定系数法求一次函数解析式的步骤
一次函数与实际问题
课堂总结
1.小明从家步行到校车站台,等候坐校车去学校,图中的折线表示这一过程中小明的路程s( km )与所花时间t( min )间的函数关系.下列说法:①他步行了1 km到校车站台;②他步行的速度是100 m/min;③他在校车站台等了6 min;④校车运行的速度是200 m/min.其中错误的是( )
A.① B.② C.③ D.④
检测目标
D
2.若一次函数y=kx+b的图象经过第一、三、四象限,则 k、b应满足( )
A.k>0,b>0
B.k>0,b<0
C.k<0,b>0
D.k<0,b<0
B
检测目标
3.一次函数y=kx+b的图象如图,则k、b的值分别为( )
(A)k=- ,b=1 (B)k=-2,b=1
(C)k= ,b=1 (D)k=2,b=1
x
y
o
1
1
B
检测目标
4.某航空公司规定,旅客乘机所携带行李的质量x( kg )与其运费y( 元 )由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量( )
A
检测目标
A.20 kg B.25 kg
C.28 kg D.30 kg
5.如图1,甲、乙两个容器内都装了一定数量的水,现将甲容器中的水匀速注入乙容器中.图2中的线段AB,CD分别表示容器中水的深度h(厘米)与注入时间t(分钟)之间的函数图象.下列结论错误的是( )
D
检测目标
A.注水前乙容器内水的高度是5厘米
B.甲容器内的水4分钟全部注入乙容器
C.注水2分钟时,甲、乙两个容器中水的深度相等
D.注水1分钟时,甲容器的水比乙容器的水深5厘米
6.若一直线与另一直线y=-3x+2交于y轴同一点,且过 (2,-6),你能求出这条直线的解析式吗?
答案:y=-4x+2
分析:直线y=-3x+2与y轴的交点为(0,2),于是得知该直线过点(0,2),(2,-6),再用待定系数法求解即可.
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
