2022年人教版八年级数学 下册 19.2.3 一次函数与方程、不等式 第2课时 一次函数与一元一次不等式 课件(共24张)
文档属性
| 名称 | 2022年人教版八年级数学 下册 19.2.3 一次函数与方程、不等式 第2课时 一次函数与一元一次不等式 课件(共24张) |
|
|
| 格式 | zip | ||
| 文件大小 | 394.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 19:03:27 | ||
图片预览





文档简介
(共24张PPT)
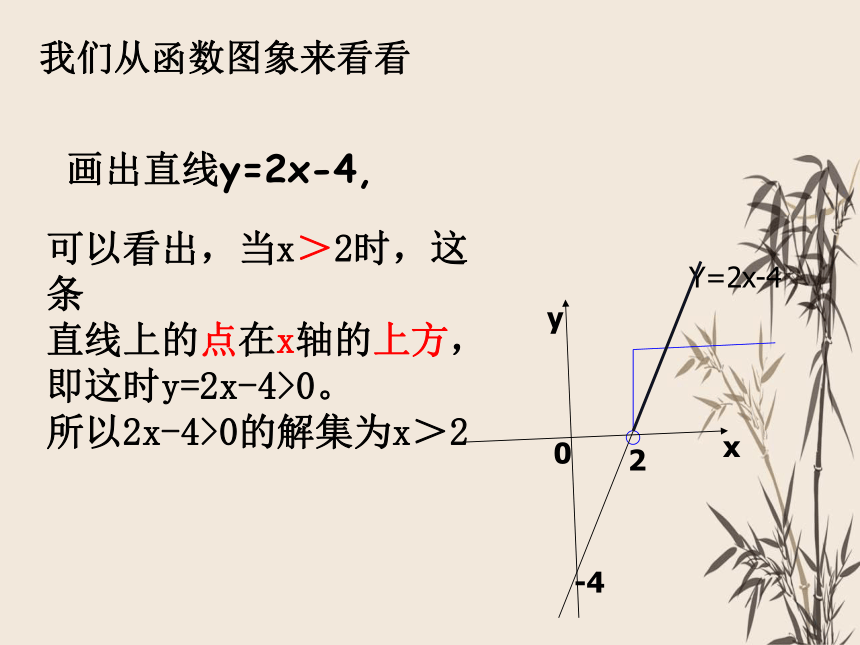
练一练:
如图:当x——————一次函数y=x-2的值为0 ,
引入
x=2是一元一次方程———————的解.
=2
x-2=0
3
2
x
-2
y
0
Y=x-2
4
当x=3时,函数y=x-2的值是-------
1
当x=4,函数y=x-2的值是--------
2
思考:当x为何值 时,
函数Y=x-2对应
的值大于0 ?
上节课我们用函数观点,从数和形两个角度
学习了一元一次方程求解问题。
19.2.3 一次函数与
方程、不等式
人教版八年级数学 下册
第2课时 一次函数与一元一次不等式
目标导航
1.认识一次函数与一元(二元)一次方程(组)、一元一次不等式之间的联系.会用函数观点解释方程和不等式及其解(解集)的意义;
2.经历用函数图象表示方程、不等式解的过程,进一步体会“以形表示数,以数解释形”的数形结合思想
认真阅读课本的内容,完成下面练习并体验知识点的形成过程。
自主研学
思考:
(1)问题1与问题2有什么关系
两个问题实际上是同一个问题,虽然结果一样,
但是表达的方式不同。因为问题1是直接求不等式2x-4 >0的解集,解得X>2,是从不等式角度进行求解。而问题2是考虑当函数 y=2x-4的函数值大于0时,自变量X的取值,是通过列不等式2x-4 > 0求解,解得X>2,是从函数的角度进行求解。
问题2:
自变量为何值时,函数y=2x-4的值大于0?
问题1:解不等式2x-4>0
探究:
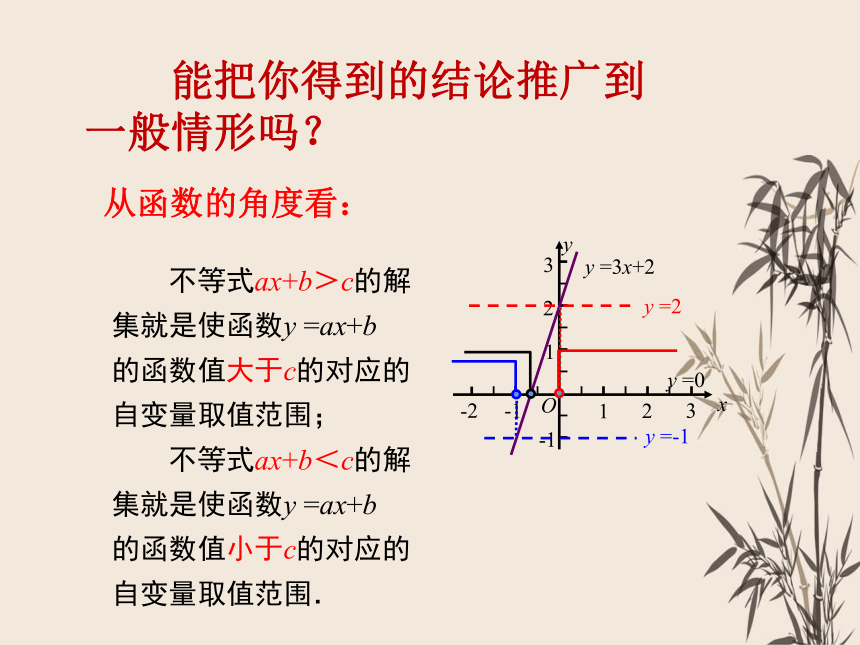
我们从函数图象来看看
画出直线y=2x-4,
-4
2
y
x
0
Y=2x-4
可以看出,当x>2时,这条
直线上的点在x轴的上方,
即这时y=2x-4>0。
所以2x-4>0的解集为x>2
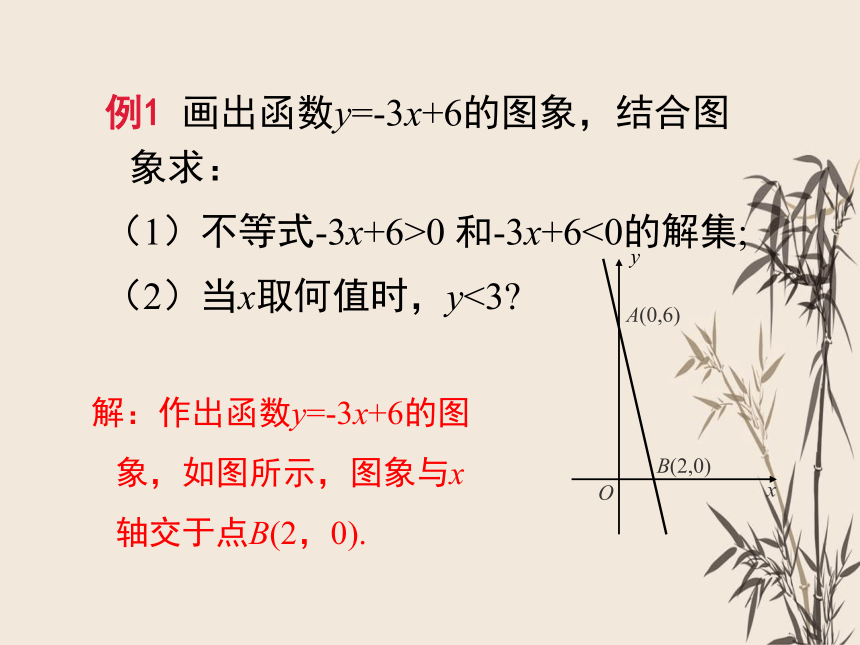
能把你得到的结论推广到一般情形吗?
不等式ax+b>c的解集就是使函数y =ax+b 的函数值大于c的对应的自变量取值范围;
不等式ax+b<c的解集就是使函数y =ax+b 的函数值小于c的对应的自变量取值范围.
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =3x+2
y =2
y =0
y =-1
从函数的角度看:
例1 画出函数y=-3x+6的图象,结合图象求:
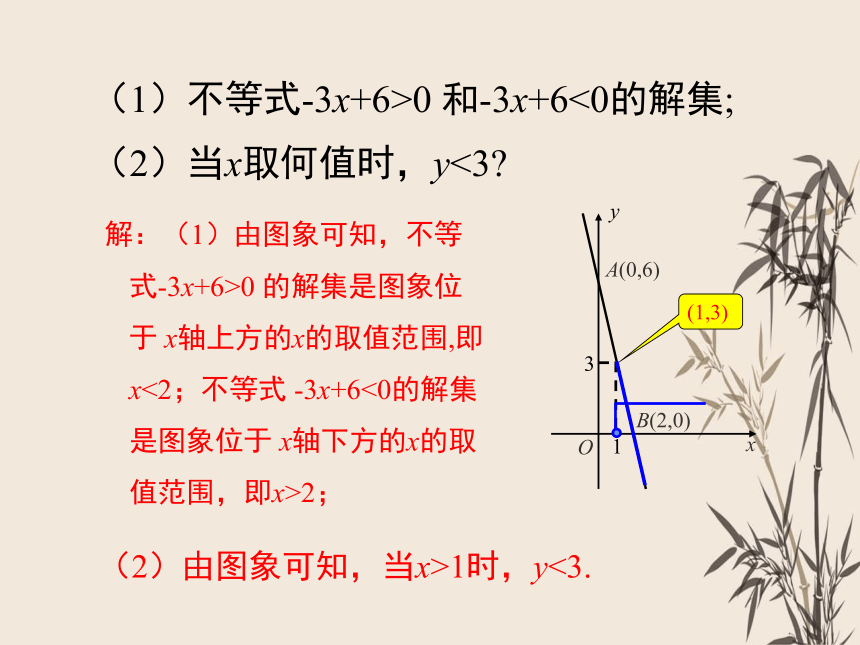
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3
解:作出函数y=-3x+6的图象,如图所示,图象与x轴交于点B(2,0).
x
O
B(2,0)
A(0,6)
y
解:(1)由图象可知,不等式-3x+6>0 的解集是图象位于 x轴上方的x的取值范围,即x<2;不等式 -3x+6<0的解集是图象位于 x轴下方的x的取值范围,即x>2;
x
O
B(2,0)
A(0,6)
3
1
(1,3)
y
(2)由图象可知,当x>1时,y<3.
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3
试一试(根据一次函数与不等式的关系填空):
求一次函数y=3x-6的函数值小于0的自变量的取值范围。
求不等式3x+8>0的解集。
(1) 解不等式3x-6<0,可看作
(2)“当自变量x取何值时,函数y=3x+8的值大于0”可看作
即学即练
-2
x
y=3x+6
y
例2 根据下列一次函数的图像,直接写出下列不等式的解集
3x+6>0
(3) –x+3 ≥0
x
y
3
y=-x+3
(2)3x+6 ≤0
X>-2
(4) –x+3<0
x≤3
X≤-2
x>3
(即y>0)
(即y≤0)
(即y<0)
(即y≥0)
1.直线 y=x-1 上的点在 x 轴上方时对应的自变量的范围是( )
A. x>1 B. x≥1 C. x<1 D. x≤1
2.已知直线 y=2x+k 与 x 轴的交点为 (-2,0),则关于x的不等式 2x+k<0 的解集是 ( )
A. x>-2 B. x≥-2 C. x<-2 D. x≤-2
A
C
即学即练
例3、试根据函数y=3x-15的性质或图象,确定取何值时:
(1)y>0; (2)y<0
解:令3x-15=0,解得,x=5
∵函数y=3x-15中k=3>0,
∴y随x的增大而增大,
∴(1)当x>5时,y>0;
(2)当x<5时,y<0。
x>2
如图是一次函数
的图象,则关于x的方程
的解为 ;关于x的不等式
的解集为 ;
的解集为 .
关于x的不等式
x=2
x<2
即学即练
例4. 我们学校做一批校徽,需要拍照,若到照相馆拍,每张需要8元;若学校自己拍,除买摄象机,需120元,每张还需成本4元,设需要拍X张,到照相馆拍需要Y1 元,学校自己拍需要Y2元。
(1)求Y1和Y2与X的函数关系式
(2)问拍这批照片到照相馆拍,费用省还是由学校自己拍费用省?请说明理由。
解:(1) Y1=8x,Y2=4x+120
(2)由图象可知,当x=30 时,两家一样,
当X>30时,照相馆省钱,
当X<30时,学校自己省钱.
30
y
x
0
Y=4x+120
Y=8x
精典例题
(1)何时哥哥追上弟弟?
(2)何时弟弟跑在哥哥前面?
(3)何时哥哥跑在弟弟前面?
(4)谁先跑过20m?谁先跑过100m?
(5 ) 你是怎样求解的?与同伴交流。
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑。已知弟弟每秒跑3m,哥哥每秒跑4m。列出函数关系式,作出函数图象,观察图象回答下列问题:
即学即练
一次函数与一元一次不等式的关系
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
函数y= ax+b的函数值
大于0(或小于0)时x
的取值范围
直线y= ax+b在X轴上方或
下方时自变量的取值范围
从数的角度看
从形的角度看
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
课堂小结
1.已知一次函数y=kx+b的图象如图所示,则不等式kx+b>0解集是 ( )
A.x>-2 B.x<-2
C.x>-1 D.x<-1
B
检测目标
2.已知直线y=2x+k与x轴的交点为(-2,0),则关于不等式2x+k<0的解集是( )
A.x>-2 B.x≥-2
C.x<-2 D.x<2
C
检测目标
3.直线y=kx+3经过点A(2,1),则不等式kx+3≥0的解集是( )
A.x≤3 B.x≥3
C.x≥-3 D.x≤0
B
检测目标
4.如右图, 一次函数
的图象
经过点 ,则关于x的不等式 的解集为________________.
分析:即求y>-2时x的取值范围
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
练一练:
如图:当x——————一次函数y=x-2的值为0 ,
引入
x=2是一元一次方程———————的解.
=2
x-2=0
3
2
x
-2
y
0
Y=x-2
4
当x=3时,函数y=x-2的值是-------
1
当x=4,函数y=x-2的值是--------
2
思考:当x为何值 时,
函数Y=x-2对应
的值大于0 ?
上节课我们用函数观点,从数和形两个角度
学习了一元一次方程求解问题。
19.2.3 一次函数与
方程、不等式
人教版八年级数学 下册
第2课时 一次函数与一元一次不等式
目标导航
1.认识一次函数与一元(二元)一次方程(组)、一元一次不等式之间的联系.会用函数观点解释方程和不等式及其解(解集)的意义;
2.经历用函数图象表示方程、不等式解的过程,进一步体会“以形表示数,以数解释形”的数形结合思想
认真阅读课本的内容,完成下面练习并体验知识点的形成过程。
自主研学
思考:
(1)问题1与问题2有什么关系
两个问题实际上是同一个问题,虽然结果一样,
但是表达的方式不同。因为问题1是直接求不等式2x-4 >0的解集,解得X>2,是从不等式角度进行求解。而问题2是考虑当函数 y=2x-4的函数值大于0时,自变量X的取值,是通过列不等式2x-4 > 0求解,解得X>2,是从函数的角度进行求解。
问题2:
自变量为何值时,函数y=2x-4的值大于0?
问题1:解不等式2x-4>0
探究:
我们从函数图象来看看
画出直线y=2x-4,
-4
2
y
x
0
Y=2x-4
可以看出,当x>2时,这条
直线上的点在x轴的上方,
即这时y=2x-4>0。
所以2x-4>0的解集为x>2
能把你得到的结论推广到一般情形吗?
不等式ax+b>c的解集就是使函数y =ax+b 的函数值大于c的对应的自变量取值范围;
不等式ax+b<c的解集就是使函数y =ax+b 的函数值小于c的对应的自变量取值范围.
3
2
1
2
1
-2
O
x
y
-1
-1
3
y =3x+2
y =2
y =0
y =-1
从函数的角度看:
例1 画出函数y=-3x+6的图象,结合图象求:
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3
解:作出函数y=-3x+6的图象,如图所示,图象与x轴交于点B(2,0).
x
O
B(2,0)
A(0,6)
y
解:(1)由图象可知,不等式-3x+6>0 的解集是图象位于 x轴上方的x的取值范围,即x<2;不等式 -3x+6<0的解集是图象位于 x轴下方的x的取值范围,即x>2;
x
O
B(2,0)
A(0,6)
3
1
(1,3)
y
(2)由图象可知,当x>1时,y<3.
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当x取何值时,y<3
试一试(根据一次函数与不等式的关系填空):
求一次函数y=3x-6的函数值小于0的自变量的取值范围。
求不等式3x+8>0的解集。
(1) 解不等式3x-6<0,可看作
(2)“当自变量x取何值时,函数y=3x+8的值大于0”可看作
即学即练
-2
x
y=3x+6
y
例2 根据下列一次函数的图像,直接写出下列不等式的解集
3x+6>0
(3) –x+3 ≥0
x
y
3
y=-x+3
(2)3x+6 ≤0
X>-2
(4) –x+3<0
x≤3
X≤-2
x>3
(即y>0)
(即y≤0)
(即y<0)
(即y≥0)
1.直线 y=x-1 上的点在 x 轴上方时对应的自变量的范围是( )
A. x>1 B. x≥1 C. x<1 D. x≤1
2.已知直线 y=2x+k 与 x 轴的交点为 (-2,0),则关于x的不等式 2x+k<0 的解集是 ( )
A. x>-2 B. x≥-2 C. x<-2 D. x≤-2
A
C
即学即练
例3、试根据函数y=3x-15的性质或图象,确定取何值时:
(1)y>0; (2)y<0
解:令3x-15=0,解得,x=5
∵函数y=3x-15中k=3>0,
∴y随x的增大而增大,
∴(1)当x>5时,y>0;
(2)当x<5时,y<0。
x>2
如图是一次函数
的图象,则关于x的方程
的解为 ;关于x的不等式
的解集为 ;
的解集为 .
关于x的不等式
x=2
x<2
即学即练
例4. 我们学校做一批校徽,需要拍照,若到照相馆拍,每张需要8元;若学校自己拍,除买摄象机,需120元,每张还需成本4元,设需要拍X张,到照相馆拍需要Y1 元,学校自己拍需要Y2元。
(1)求Y1和Y2与X的函数关系式
(2)问拍这批照片到照相馆拍,费用省还是由学校自己拍费用省?请说明理由。
解:(1) Y1=8x,Y2=4x+120
(2)由图象可知,当x=30 时,两家一样,
当X>30时,照相馆省钱,
当X<30时,学校自己省钱.
30
y
x
0
Y=4x+120
Y=8x
精典例题
(1)何时哥哥追上弟弟?
(2)何时弟弟跑在哥哥前面?
(3)何时哥哥跑在弟弟前面?
(4)谁先跑过20m?谁先跑过100m?
(5 ) 你是怎样求解的?与同伴交流。
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑。已知弟弟每秒跑3m,哥哥每秒跑4m。列出函数关系式,作出函数图象,观察图象回答下列问题:
即学即练
一次函数与一元一次不等式的关系
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
函数y= ax+b的函数值
大于0(或小于0)时x
的取值范围
直线y= ax+b在X轴上方或
下方时自变量的取值范围
从数的角度看
从形的角度看
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
课堂小结
1.已知一次函数y=kx+b的图象如图所示,则不等式kx+b>0解集是 ( )
A.x>-2 B.x<-2
C.x>-1 D.x<-1
B
检测目标
2.已知直线y=2x+k与x轴的交点为(-2,0),则关于不等式2x+k<0的解集是( )
A.x>-2 B.x≥-2
C.x<-2 D.x<2
C
检测目标
3.直线y=kx+3经过点A(2,1),则不等式kx+3≥0的解集是( )
A.x≤3 B.x≥3
C.x≥-3 D.x≤0
B
检测目标
4.如右图, 一次函数
的图象
经过点 ,则关于x的不等式 的解集为________________.
分析:即求y>-2时x的取值范围
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
