人教版数学六年级下册 3.1.3圆柱的体积 课件(29张PPT)
文档属性
| 名称 | 人教版数学六年级下册 3.1.3圆柱的体积 课件(29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 21:38:47 | ||
图片预览





文档简介
(共29张PPT)
3.1.3圆柱的体积
教学目标
1.通过切割圆柱体,拼成近似的长方体,从而推导出圆柱的体积公式这一教学过程,向同学们渗透转化思想。
2.通过圆柱体体积公式的推导,培养同学们的分析推理能力。
3.理解圆柱体体积公式的推导过程,掌握计算公式;会运用公式计算圆柱的体积。
(1)什么叫体积?怎样求长方体的体积?
长
v
=a b h
v
3
正
=a
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
V=s h
底
长a
宽b
高h
棱 长 a
今天,我们能不能也用这个思路研究圆柱的体积呢?
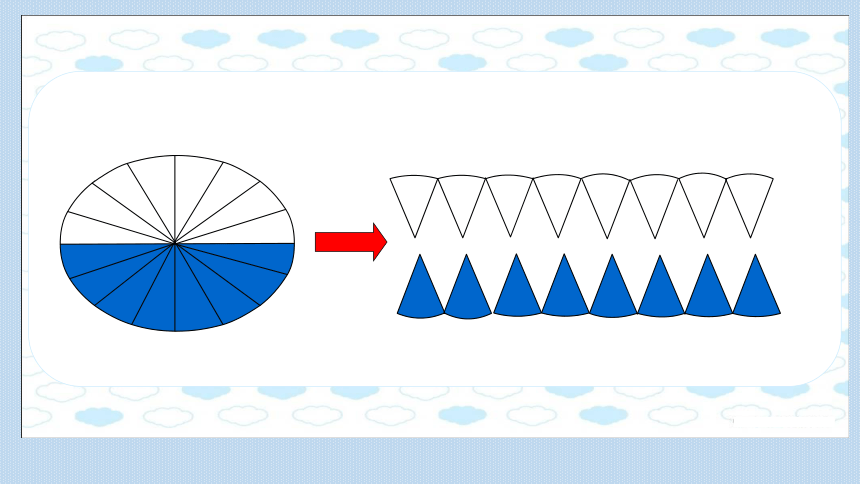
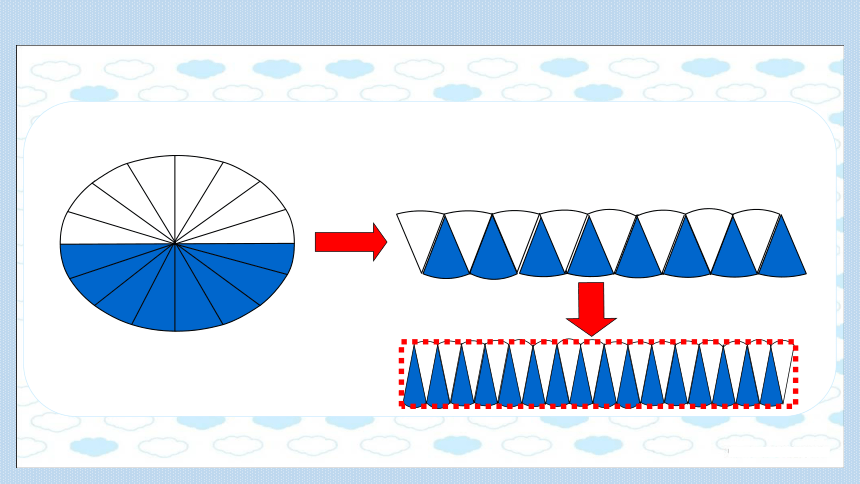
(2)圆的面积公式是怎样推导的
底面积
高
探究点 1
圆柱的体积的意义和计算公式的推导
各小组,利用手中的学具进行操作、推导并写出推导过程。
小组合作:
你发现了什么?
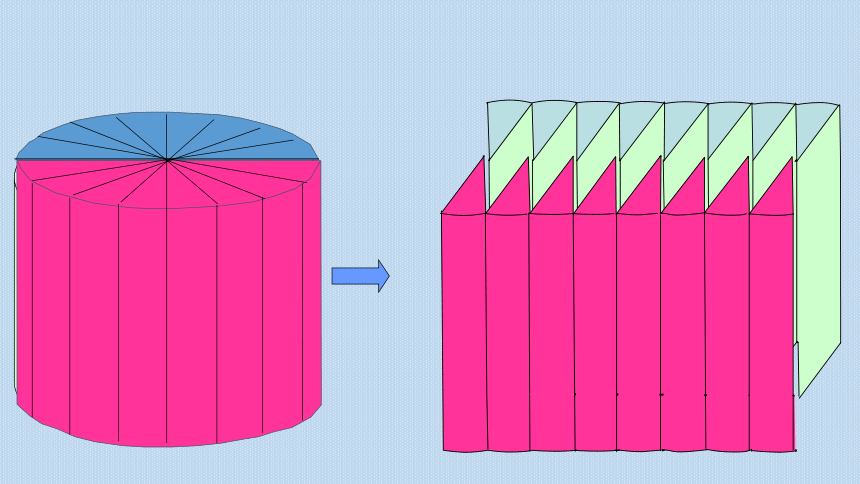
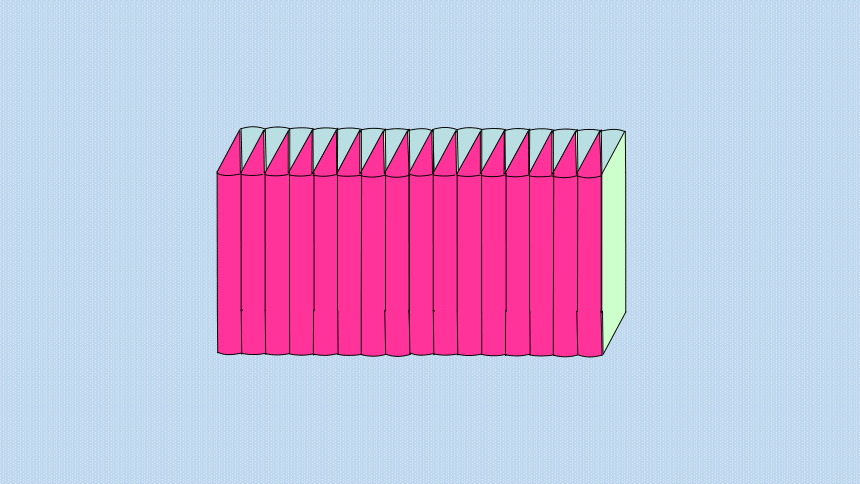
分成的扇形越多,拼成的立体图形越接近长方体。
这个长方体的底面积等于圆柱( )高等于圆柱的( )。
长方体的体积= 底面积 × 高
V=sh
高
底面圆的面积
圆柱的体积= ×
底面圆的面积
高
V =sh=πr2h
如果知道圆柱的底面半径r和高h,
你能写出圆柱的体积公式吗?
1. 一个圆柱的体积是80cm ,底面积是16cm2。它的高是多少厘米?
80 ÷16 =5(cm)
答:它的高是5cm。
巩固拓展,乐于运用
2. 一个圆柱形粮囤,从里面量得底面半径是1.5m,高2m。如果每立方米玉米约重750kg,这个粮囤能装多少吨玉米?
粮囤的容积:3.14×1.5 ×2
=3.14×2.25×2
=7.065×2
=14.13 (m )
粮囤所装玉米:14.13×750÷1000
=10597.5÷1000
=10.5975(吨)
答:这个粮囤能装10.5975吨。
请你想一想,要知道这个粮囤能装多少吨玉米,就要知道这个粮囤什么?
巩固拓展,乐于运用
3. 一个圆柱形玻璃容器的底面直径是10cm,把一块完全浸泡在这个容器的水中的铁块取出后,水面下降 2cm。这块铁块的体积是多少?
3.14×(10÷2)×2
=3.14×5 ×2
=3.14×25×2
=78.5×2
=157(cm )
2
答:这块铁皮的体积是157cm 。
请你想一想,如何求这块铁块的体积?
绿色圃中小学教育网http://www.Lspjy.com
1.求下面各圆柱的侧面积。
(1)底面周长是1.6m,高是0.7m。
侧面积=1.6×0.7=1.12(m )
(2)底面半径是3.2dm,高5dm。
侧面积=3.14×3.2×2×5=100.48(dm )
课堂练习
2.下列说法正确的是( )。
A.圆柱的体积一定比表面积大
B.圆柱的高不变,底面半径扩大到原来的2倍,体积就扩大到原来的2倍
C.如果两个圆柱的体积相等,那么它们的高也相等
D.如果两个圆的周长相等,那么面积也相等
D
辨析:圆的周长相等,半径就相等,面积也相等。
3.一根圆柱形的木料,底面积是320平方厘米,高是1.8米。这根木料的体积是多少?
1.8米=180厘米
320×180=57600(立方厘米)
答:它的体积是57600立方厘米。
320平方厘米=0.032平方米
0.032 ×1.8=0.0576(立方米)
答:这根木料的体积是0.0576立方米。
4.一根圆柱形木料,底面积为 75cm2,长 90cm。它的体积是多少?
V圆柱=S底h
=75×90
答:它的体积是6750立方厘米
=6750(立方厘米)
拓展延伸
1. 广告公司制作了一个底面直径是1.5m、高2.5m的圆柱形灯箱。可以张贴多大面积的海报?
分析:同上一题一样,也是求圆柱侧面面积的题型。
答:可张贴海报的面积为
S=π·1.5×2.5=3.75π≈11.775(m3)
2.一个圆柱形钢管,底面周长是25.12分米,高和直径相等,它的体积是多少?
(提示:先求底面积,最后求体积)
课堂小结
(1)已知圆的半径和高,怎样求圆柱的体积?
(2)已知圆的直径和高,怎样求圆柱的体积?
(3)已知圆的周长和高,怎样求圆柱的体积?
(1)已知圆的半径和高:
V=∏r2h
(2)已知圆的直径和高:
V=∏( )2h
d
2
(3)已知圆的周长和高:
V=∏(C÷d÷2 )2h
3.1.3圆柱的体积
教学目标
1.通过切割圆柱体,拼成近似的长方体,从而推导出圆柱的体积公式这一教学过程,向同学们渗透转化思想。
2.通过圆柱体体积公式的推导,培养同学们的分析推理能力。
3.理解圆柱体体积公式的推导过程,掌握计算公式;会运用公式计算圆柱的体积。
(1)什么叫体积?怎样求长方体的体积?
长
v
=a b h
v
3
正
=a
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
V=s h
底
长a
宽b
高h
棱 长 a
今天,我们能不能也用这个思路研究圆柱的体积呢?
(2)圆的面积公式是怎样推导的
底面积
高
探究点 1
圆柱的体积的意义和计算公式的推导
各小组,利用手中的学具进行操作、推导并写出推导过程。
小组合作:
你发现了什么?
分成的扇形越多,拼成的立体图形越接近长方体。
这个长方体的底面积等于圆柱( )高等于圆柱的( )。
长方体的体积= 底面积 × 高
V=sh
高
底面圆的面积
圆柱的体积= ×
底面圆的面积
高
V =sh=πr2h
如果知道圆柱的底面半径r和高h,
你能写出圆柱的体积公式吗?
1. 一个圆柱的体积是80cm ,底面积是16cm2。它的高是多少厘米?
80 ÷16 =5(cm)
答:它的高是5cm。
巩固拓展,乐于运用
2. 一个圆柱形粮囤,从里面量得底面半径是1.5m,高2m。如果每立方米玉米约重750kg,这个粮囤能装多少吨玉米?
粮囤的容积:3.14×1.5 ×2
=3.14×2.25×2
=7.065×2
=14.13 (m )
粮囤所装玉米:14.13×750÷1000
=10597.5÷1000
=10.5975(吨)
答:这个粮囤能装10.5975吨。
请你想一想,要知道这个粮囤能装多少吨玉米,就要知道这个粮囤什么?
巩固拓展,乐于运用
3. 一个圆柱形玻璃容器的底面直径是10cm,把一块完全浸泡在这个容器的水中的铁块取出后,水面下降 2cm。这块铁块的体积是多少?
3.14×(10÷2)×2
=3.14×5 ×2
=3.14×25×2
=78.5×2
=157(cm )
2
答:这块铁皮的体积是157cm 。
请你想一想,如何求这块铁块的体积?
绿色圃中小学教育网http://www.Lspjy.com
1.求下面各圆柱的侧面积。
(1)底面周长是1.6m,高是0.7m。
侧面积=1.6×0.7=1.12(m )
(2)底面半径是3.2dm,高5dm。
侧面积=3.14×3.2×2×5=100.48(dm )
课堂练习
2.下列说法正确的是( )。
A.圆柱的体积一定比表面积大
B.圆柱的高不变,底面半径扩大到原来的2倍,体积就扩大到原来的2倍
C.如果两个圆柱的体积相等,那么它们的高也相等
D.如果两个圆的周长相等,那么面积也相等
D
辨析:圆的周长相等,半径就相等,面积也相等。
3.一根圆柱形的木料,底面积是320平方厘米,高是1.8米。这根木料的体积是多少?
1.8米=180厘米
320×180=57600(立方厘米)
答:它的体积是57600立方厘米。
320平方厘米=0.032平方米
0.032 ×1.8=0.0576(立方米)
答:这根木料的体积是0.0576立方米。
4.一根圆柱形木料,底面积为 75cm2,长 90cm。它的体积是多少?
V圆柱=S底h
=75×90
答:它的体积是6750立方厘米
=6750(立方厘米)
拓展延伸
1. 广告公司制作了一个底面直径是1.5m、高2.5m的圆柱形灯箱。可以张贴多大面积的海报?
分析:同上一题一样,也是求圆柱侧面面积的题型。
答:可张贴海报的面积为
S=π·1.5×2.5=3.75π≈11.775(m3)
2.一个圆柱形钢管,底面周长是25.12分米,高和直径相等,它的体积是多少?
(提示:先求底面积,最后求体积)
课堂小结
(1)已知圆的半径和高,怎样求圆柱的体积?
(2)已知圆的直径和高,怎样求圆柱的体积?
(3)已知圆的周长和高,怎样求圆柱的体积?
(1)已知圆的半径和高:
V=∏r2h
(2)已知圆的直径和高:
V=∏( )2h
d
2
(3)已知圆的周长和高:
V=∏(C÷d÷2 )2h
