华东师大版八年级下册数学 19.2.2 菱形的判定 课件(共19张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 19.2.2 菱形的判定 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 755.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
菱形的判定
感受生活
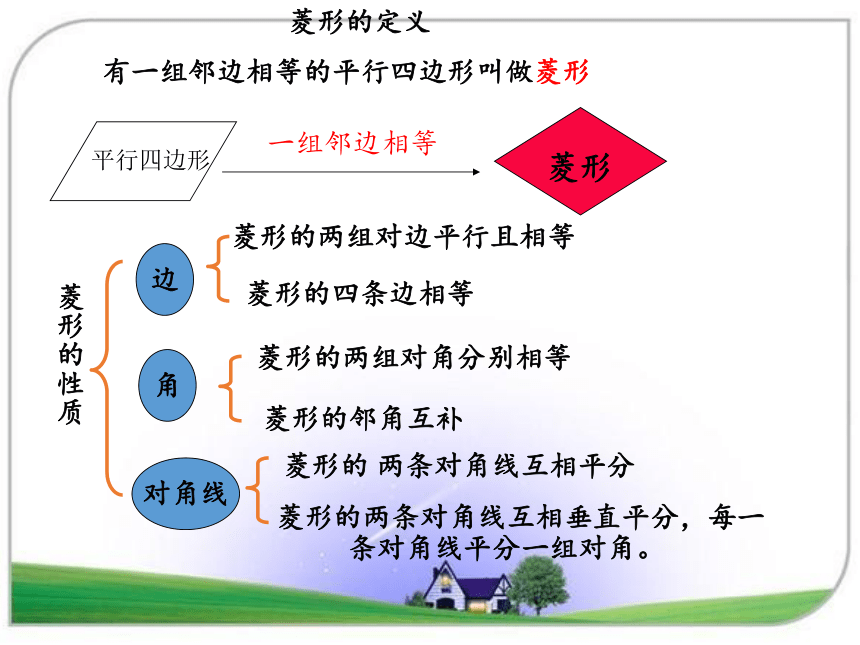
一组邻边相等
有一组邻边相等的平行四边形叫做菱形
平行四边形
边
对角线
角
菱形的定义
菱形的性质
菱形
菱形的 两条对角线互相平分
菱形的两组对边平行且相等
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,每一条对角线平分一组对角。
学习目标
1、掌握菱形的判定定理及证明方法。
2、学会运用菱形的判定解决一些问题;进一步发展合情推理能力;逐步掌握说理的基本方法。
3、经历探索菱形判定的过程,发展主动探索、研究的习惯。
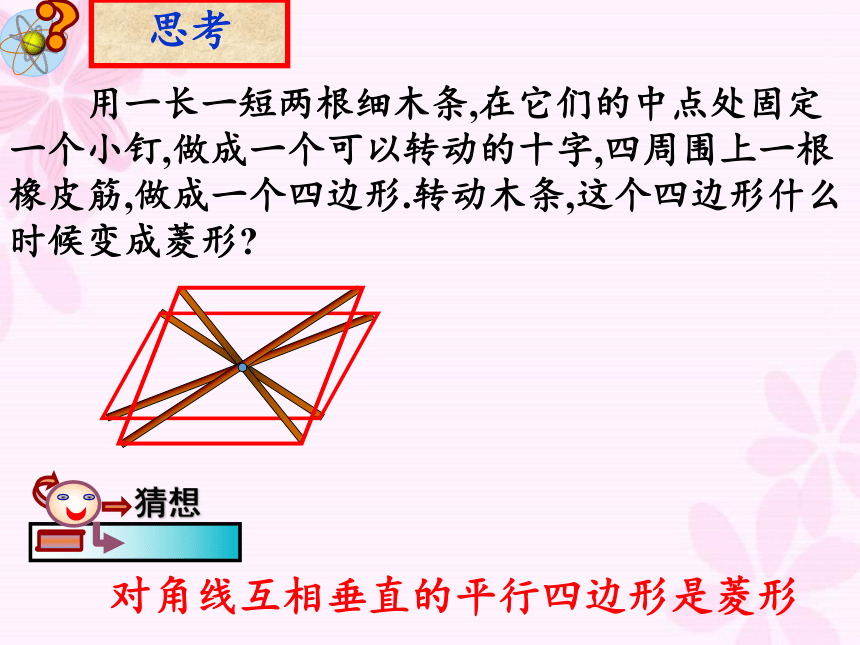
思考
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形
猜想
对角线互相垂直的平行四边形是菱形.
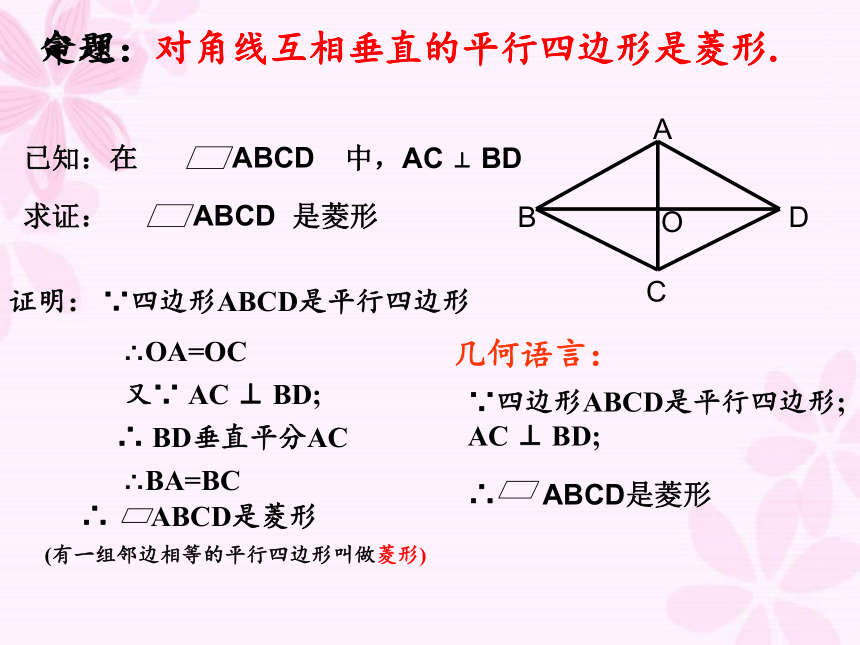
命题:对角线互相垂直的平行四边形是菱形.
已知:在 中,AC ⊥ BD
ABCD
ABCD
求证: 是菱形
证明:
∴ ABCD是菱形
又∵ AC ⊥ BD;
∵四边形ABCD是平行四边形
∴OA=OC
∴BA=BC
A
B
C
D
O
定理:对角线互相垂直的平行四边形是菱形.
几何语言:
∵四边形ABCD是平行四边形; AC ⊥ BD;
∴ ABCD是菱形
(有一组邻边相等的平行四边形叫做菱形)
∴ BD垂直平分AC
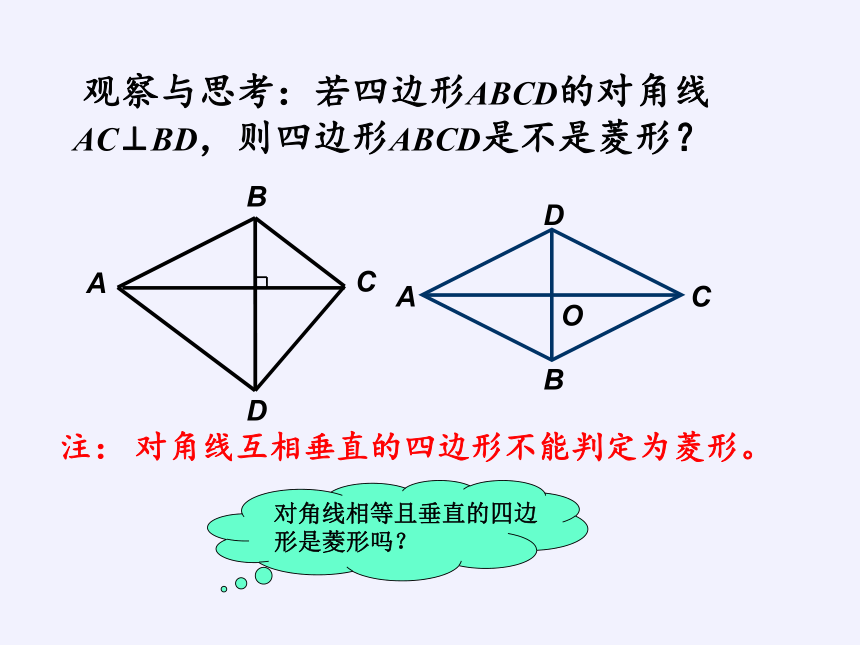
观察与思考:若四边形ABCD的对角线AC⊥BD,则四边形ABCD是不是菱形?
注: 对角线互相垂直的四边形不能判定为菱形。
D
C
A
B
A
B
C
D
O
对角线相等且垂直的四边形是菱形吗?
判断下列说法是否正确:
1.有一条对角线平分一组对角的四边形是菱形
3.对角线相等且互相平分的四边形是菱形
矩形
2.对角线互相垂直,且一条对角线平分一组对角的四边形是菱形
4.对角线互相垂直平分的四边形是菱形
菱形常用的判定方法
1、有一组邻边相等的平行四边形叫做菱形。
3、对角线互相垂直的平行四边形是菱形。
4、对角线互相垂直平分的四边形是菱形
2、有四条边相等的四边形是菱形。
1.下列命题中正确的是( )
A.一组邻边相等的四边形是菱形 B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形 D.四个角相等的四边形是菱形
C
2.对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形 C.菱形 D.以上都不对
C
3.下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分 B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD D.AB=CD,AD=BC,AC⊥BD
C
做一做
有人说下列三个图形都是菱形,你相信吗
5
5
3
4
3
4
3
4
3
4
∟
5
5
5
5
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
小明为班级设计了一个班徽,图中有一个菱形。为了检验小明所画的菱形是否准确,请你以带有刻度的三角尺为工具,设计一个检验方案。
A
B
C
D
O
例1:如图, □ ABCD的两条对角线AC、BD相交于点O,AB= , AO=2,OB=1.
(1)AC,BD互相垂直吗?为什么?
(2)四边形ABCD是菱形吗?为什么?
A
B
C
D
O
解:(1)∵ AB= ,AO=2,OB=1.
根据勾股定理逆定理
∴∠AOB=90° ∴AC⊥BD.
(2)∵ 四边形ABCD是平行四边形,
且AC⊥BD
∴四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形).
5
2
1
例2、
已知:如图(1), □ ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形
A
B
F
C
D
E
O
C
思考:如图(2),若将例2中的“□ ABCD”改成“矩形ABCD”,其他条件不变,若AB=4厘米,BC=8厘米,求四边形AFCE的面积。
(1)
A
E
F
B
D
(2)
O
1、进一步熟练了菱形的判定方法;
2、能灵活得看待每一个题目,学会一题多证,一题多解;
3、利用所学知识,会解决生活中的实际问题。
感悟与收获
判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.
√
╳
╳
╳
做一做
□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形。
A
B
C
D
O
菱
矩
矩
菱
作业:
A组:P112 习题4、6
B组:P112 习题3、4
谢 谢
菱形的判定
感受生活
一组邻边相等
有一组邻边相等的平行四边形叫做菱形
平行四边形
边
对角线
角
菱形的定义
菱形的性质
菱形
菱形的 两条对角线互相平分
菱形的两组对边平行且相等
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,每一条对角线平分一组对角。
学习目标
1、掌握菱形的判定定理及证明方法。
2、学会运用菱形的判定解决一些问题;进一步发展合情推理能力;逐步掌握说理的基本方法。
3、经历探索菱形判定的过程,发展主动探索、研究的习惯。
思考
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形
猜想
对角线互相垂直的平行四边形是菱形.
命题:对角线互相垂直的平行四边形是菱形.
已知:在 中,AC ⊥ BD
ABCD
ABCD
求证: 是菱形
证明:
∴ ABCD是菱形
又∵ AC ⊥ BD;
∵四边形ABCD是平行四边形
∴OA=OC
∴BA=BC
A
B
C
D
O
定理:对角线互相垂直的平行四边形是菱形.
几何语言:
∵四边形ABCD是平行四边形; AC ⊥ BD;
∴ ABCD是菱形
(有一组邻边相等的平行四边形叫做菱形)
∴ BD垂直平分AC
观察与思考:若四边形ABCD的对角线AC⊥BD,则四边形ABCD是不是菱形?
注: 对角线互相垂直的四边形不能判定为菱形。
D
C
A
B
A
B
C
D
O
对角线相等且垂直的四边形是菱形吗?
判断下列说法是否正确:
1.有一条对角线平分一组对角的四边形是菱形
3.对角线相等且互相平分的四边形是菱形
矩形
2.对角线互相垂直,且一条对角线平分一组对角的四边形是菱形
4.对角线互相垂直平分的四边形是菱形
菱形常用的判定方法
1、有一组邻边相等的平行四边形叫做菱形。
3、对角线互相垂直的平行四边形是菱形。
4、对角线互相垂直平分的四边形是菱形
2、有四条边相等的四边形是菱形。
1.下列命题中正确的是( )
A.一组邻边相等的四边形是菱形 B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形 D.四个角相等的四边形是菱形
C
2.对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形 C.菱形 D.以上都不对
C
3.下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分 B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD D.AB=CD,AD=BC,AC⊥BD
C
做一做
有人说下列三个图形都是菱形,你相信吗
5
5
3
4
3
4
3
4
3
4
∟
5
5
5
5
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
小明为班级设计了一个班徽,图中有一个菱形。为了检验小明所画的菱形是否准确,请你以带有刻度的三角尺为工具,设计一个检验方案。
A
B
C
D
O
例1:如图, □ ABCD的两条对角线AC、BD相交于点O,AB= , AO=2,OB=1.
(1)AC,BD互相垂直吗?为什么?
(2)四边形ABCD是菱形吗?为什么?
A
B
C
D
O
解:(1)∵ AB= ,AO=2,OB=1.
根据勾股定理逆定理
∴∠AOB=90° ∴AC⊥BD.
(2)∵ 四边形ABCD是平行四边形,
且AC⊥BD
∴四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形).
5
2
1
例2、
已知:如图(1), □ ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形
A
B
F
C
D
E
O
C
思考:如图(2),若将例2中的“□ ABCD”改成“矩形ABCD”,其他条件不变,若AB=4厘米,BC=8厘米,求四边形AFCE的面积。
(1)
A
E
F
B
D
(2)
O
1、进一步熟练了菱形的判定方法;
2、能灵活得看待每一个题目,学会一题多证,一题多解;
3、利用所学知识,会解决生活中的实际问题。
感悟与收获
判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.
√
╳
╳
╳
做一做
□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形。
A
B
C
D
O
菱
矩
矩
菱
作业:
A组:P112 习题4、6
B组:P112 习题3、4
谢 谢
