人教版数学六年级下册 3.1.2圆柱的表面积 课件(21张PPT)
文档属性
| 名称 | 人教版数学六年级下册 3.1.2圆柱的表面积 课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-20 22:17:02 | ||
图片预览






文档简介
(共21张PPT)
3.1.2圆柱的表面积
根据具体情境,灵活运用圆柱表面积的计算方法解决生活中一些简单的问题,使学生感受到数学与生活的密切联系
通过想象、操作等活动,知道圆柱侧面展开后可以是一个长方形,加深对圆柱特征的认识,发展空间观念。
3. 结合具体情境和动手操作,探索圆柱侧面积的计算方法,掌握圆柱侧面积和表面积的计算方法,能正确计算圆柱的侧面积和表面积。
1.求下面各圆的周长(单位:厘米)
(1)d=4 (2) r=1.5
2.求下面各圆的面积(单位:厘米)
(1)d=2 (2)c=12.56
知识回顾
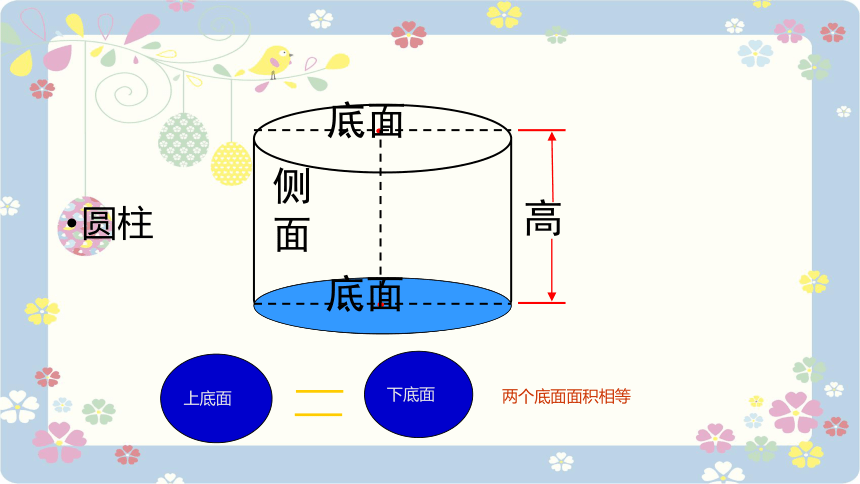
圆柱
侧 面
高
底面
底面
下底面
上底面
两个底面面积相等
一、预习自检环节:
1.我们学过哪些平面图形?
2.圆的周长和面积怎样求呢?
r=3cm d=( )=( )cm
c=( )=( )cm
s=( )=( )cm2
3.我们学过哪些立体图形?长方体和正方体
的表面积指什么?怎样计算?
4.生活中哪些物体是圆柱体呢?
6
2×3
2×3.14×3
18.84
3.14×32
28.26
想一想,能否将这个曲面转化成我们学过的平面图形?开动脑筋想一想它的侧面该怎样计算?
圆柱的侧面积=底面周长×高
用字母表示为:
直接计算:S =Ch
侧
利用直径计算:S =πdh
侧
利用半径计算:S =2πrh
侧
圆柱的侧面是一个曲面,怎样计算它的面积呢?
要计算圆柱的侧面积需要知道哪两个条件?
用字母怎么表示呢?
圆柱的侧面积=长方形的面积
=长 × 宽
=圆柱的底面周长 × 高
二、探究新知
高
底面的周长
侧面
底面的周长
高
二、探究新知
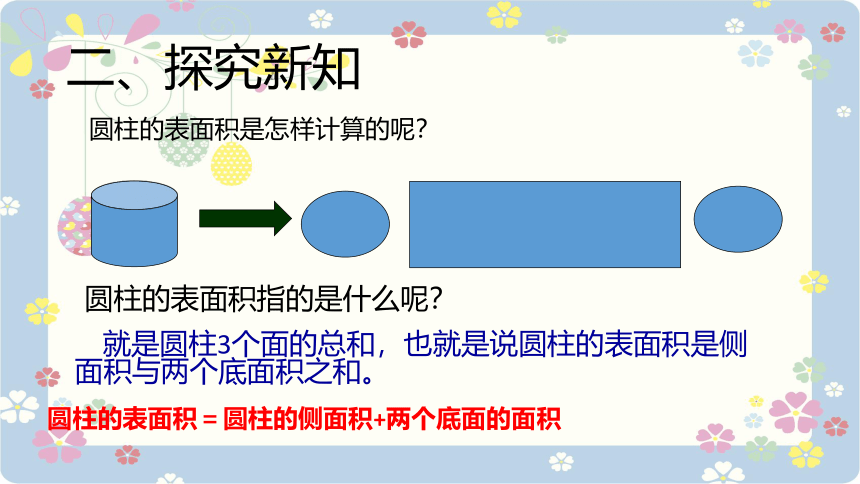
圆柱的表面积是怎样计算的呢?
圆柱的表面积指的是什么呢?
就是圆柱3个面的总和,也就是说圆柱的表面积是侧面积与两个底面积之和。
圆柱的表面积=圆柱的侧面积+两个底面的面积
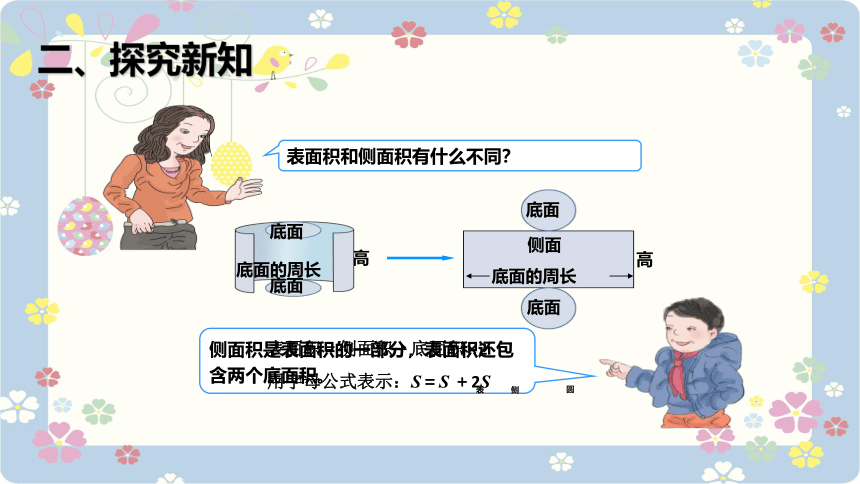
侧面积是表面积的一部分,表面积还包含两个底面积。
表面积=侧面积+底面积×2
用字母公式表示:S=S +2S
表
侧
圆
表面积和侧面积有什么不同?
二、探究新知
高
底面
底面
底面的周长
底面
底面
高
底面的周长
侧面
一顶圆柱形厨师帽,高30cm,帽顶直径20cm,做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数。)
(1)帽子的侧面积:3.14×20×30=1884(cm2 )
(2)帽顶的面积:3.14×(20÷2)=314(cm2 )
2
(3)需要用的面料:1884+314=2198≈2200(cm2 )
答:做这样一顶帽子至少要用2200cm2的面料。
想一想:求多少面料就是求什么?
“没有底”的帽子如果展开,它由哪几部分组成?
实际使用的面料要比计算的结果多一些,所以这类问题往往用“进一法”取近似数。
二、探究新知
“没有底”的帽子的展开图,它是由一个底面和一个侧面组成。
讨论:如果一段圆柱形的木头,截 成两截,它的表面积会有什么变化呢?
三、练一练
1.下面是一个生日蛋糕,地盘是塑料板。(单位:厘米)
(1)为生日蛋糕选择一个合适的蛋糕盒。
(2)做这个生日蛋糕需要多少硬纸板?
2、求圆柱的表面积。
3、如图,做一个无盖的圆柱形铁皮水桶,底面直径为4dm,高为5dm,至少需要用多大面积的铁皮?
侧面积+一个底面积
侧面积:
底面积:
表面积:
3.14×4×5=62.8(dm2)
3.14×(4÷2)2=12.56(dm2)
62.8+12.56=75.36(dm2)
4dm
5dm
答:至少需要75.36平方分米的铁皮。
1、修建一个圆柱形的水池,底面直径
是6m,深1.2m。在池的内壁与下底面
抹上水泥,抹水泥部分的面积是多少
平方米?
四、拓展延伸
2、把一块圆柱形的钢材沿横截面截成3段
表面积增加12平方厘米,这块钢材的底
面积是多少平方厘米?
1、一个圆柱形水池,水池内壁和底部都镶上磁砖,
水池内部底面周长25.12m,池深1.2m,镶磁砖的
面积是多少平方米?
求圆柱侧面积和一个底面积
底面积:3.14×(25.12÷3.14÷2)2=50.24(m2)
侧面积:25.12×1.2=30.144(m2)
表面积:30.144+50.24=80.384(m2)
五、课堂练习
2、油桶的表面要刷上防锈油漆,每平方
米需用防锈油漆0.2kg,漆一个油桶
大约需要多少防锈油漆?(结果保留
两位小数)
求圆柱侧面积和两个底面积
侧面积:3.14×0.6×1=1.884(m2)
底面积:3.14×(0.6÷2)2×2=0.5652(m2)
表面积:1.884+0.5652=2.4492(m2)
油漆:2.4492×0.2≈0.49(kg)
3、一个圆柱体的侧面展开是个边长9.42 cm的正方形,这个圆柱体的表面积是多少cm2?(得数保留两位小数)
9.42×9.42 + 3.14×(9.42÷3.14÷2)2×2
=88.728 + 3.14×2.25×2
=102.858
≈102.86( cm2 )
答:这个圆柱体的表面积是102.86 cm2。
4、一个圆柱体的侧面积是226.08 cm2,底面半径4 cm,它的高是多少?
226.08÷(2×3.14×4)
=226.08÷25.12
=9(cm)
答:它的高是9 cm。
本节课,你又学会了什么?还有疑问吗?
在解决实际问题中,要根据实际情况,确定
求圆柱的侧面积或表面积。
六、课堂总结
3.1.2圆柱的表面积
根据具体情境,灵活运用圆柱表面积的计算方法解决生活中一些简单的问题,使学生感受到数学与生活的密切联系
通过想象、操作等活动,知道圆柱侧面展开后可以是一个长方形,加深对圆柱特征的认识,发展空间观念。
3. 结合具体情境和动手操作,探索圆柱侧面积的计算方法,掌握圆柱侧面积和表面积的计算方法,能正确计算圆柱的侧面积和表面积。
1.求下面各圆的周长(单位:厘米)
(1)d=4 (2) r=1.5
2.求下面各圆的面积(单位:厘米)
(1)d=2 (2)c=12.56
知识回顾
圆柱
侧 面
高
底面
底面
下底面
上底面
两个底面面积相等
一、预习自检环节:
1.我们学过哪些平面图形?
2.圆的周长和面积怎样求呢?
r=3cm d=( )=( )cm
c=( )=( )cm
s=( )=( )cm2
3.我们学过哪些立体图形?长方体和正方体
的表面积指什么?怎样计算?
4.生活中哪些物体是圆柱体呢?
6
2×3
2×3.14×3
18.84
3.14×32
28.26
想一想,能否将这个曲面转化成我们学过的平面图形?开动脑筋想一想它的侧面该怎样计算?
圆柱的侧面积=底面周长×高
用字母表示为:
直接计算:S =Ch
侧
利用直径计算:S =πdh
侧
利用半径计算:S =2πrh
侧
圆柱的侧面是一个曲面,怎样计算它的面积呢?
要计算圆柱的侧面积需要知道哪两个条件?
用字母怎么表示呢?
圆柱的侧面积=长方形的面积
=长 × 宽
=圆柱的底面周长 × 高
二、探究新知
高
底面的周长
侧面
底面的周长
高
二、探究新知
圆柱的表面积是怎样计算的呢?
圆柱的表面积指的是什么呢?
就是圆柱3个面的总和,也就是说圆柱的表面积是侧面积与两个底面积之和。
圆柱的表面积=圆柱的侧面积+两个底面的面积
侧面积是表面积的一部分,表面积还包含两个底面积。
表面积=侧面积+底面积×2
用字母公式表示:S=S +2S
表
侧
圆
表面积和侧面积有什么不同?
二、探究新知
高
底面
底面
底面的周长
底面
底面
高
底面的周长
侧面
一顶圆柱形厨师帽,高30cm,帽顶直径20cm,做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数。)
(1)帽子的侧面积:3.14×20×30=1884(cm2 )
(2)帽顶的面积:3.14×(20÷2)=314(cm2 )
2
(3)需要用的面料:1884+314=2198≈2200(cm2 )
答:做这样一顶帽子至少要用2200cm2的面料。
想一想:求多少面料就是求什么?
“没有底”的帽子如果展开,它由哪几部分组成?
实际使用的面料要比计算的结果多一些,所以这类问题往往用“进一法”取近似数。
二、探究新知
“没有底”的帽子的展开图,它是由一个底面和一个侧面组成。
讨论:如果一段圆柱形的木头,截 成两截,它的表面积会有什么变化呢?
三、练一练
1.下面是一个生日蛋糕,地盘是塑料板。(单位:厘米)
(1)为生日蛋糕选择一个合适的蛋糕盒。
(2)做这个生日蛋糕需要多少硬纸板?
2、求圆柱的表面积。
3、如图,做一个无盖的圆柱形铁皮水桶,底面直径为4dm,高为5dm,至少需要用多大面积的铁皮?
侧面积+一个底面积
侧面积:
底面积:
表面积:
3.14×4×5=62.8(dm2)
3.14×(4÷2)2=12.56(dm2)
62.8+12.56=75.36(dm2)
4dm
5dm
答:至少需要75.36平方分米的铁皮。
1、修建一个圆柱形的水池,底面直径
是6m,深1.2m。在池的内壁与下底面
抹上水泥,抹水泥部分的面积是多少
平方米?
四、拓展延伸
2、把一块圆柱形的钢材沿横截面截成3段
表面积增加12平方厘米,这块钢材的底
面积是多少平方厘米?
1、一个圆柱形水池,水池内壁和底部都镶上磁砖,
水池内部底面周长25.12m,池深1.2m,镶磁砖的
面积是多少平方米?
求圆柱侧面积和一个底面积
底面积:3.14×(25.12÷3.14÷2)2=50.24(m2)
侧面积:25.12×1.2=30.144(m2)
表面积:30.144+50.24=80.384(m2)
五、课堂练习
2、油桶的表面要刷上防锈油漆,每平方
米需用防锈油漆0.2kg,漆一个油桶
大约需要多少防锈油漆?(结果保留
两位小数)
求圆柱侧面积和两个底面积
侧面积:3.14×0.6×1=1.884(m2)
底面积:3.14×(0.6÷2)2×2=0.5652(m2)
表面积:1.884+0.5652=2.4492(m2)
油漆:2.4492×0.2≈0.49(kg)
3、一个圆柱体的侧面展开是个边长9.42 cm的正方形,这个圆柱体的表面积是多少cm2?(得数保留两位小数)
9.42×9.42 + 3.14×(9.42÷3.14÷2)2×2
=88.728 + 3.14×2.25×2
=102.858
≈102.86( cm2 )
答:这个圆柱体的表面积是102.86 cm2。
4、一个圆柱体的侧面积是226.08 cm2,底面半径4 cm,它的高是多少?
226.08÷(2×3.14×4)
=226.08÷25.12
=9(cm)
答:它的高是9 cm。
本节课,你又学会了什么?还有疑问吗?
在解决实际问题中,要根据实际情况,确定
求圆柱的侧面积或表面积。
六、课堂总结
