2021-2022学年鲁教版(五四制)八年级数学下册6.3正方形的性质与判定 同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学下册6.3正方形的性质与判定 同步练习题(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 165.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 00:00:00 | ||
图片预览





文档简介
2021-2022学年鲁教版八年级数学下册《6-3正方形的性质与判定》同步练习题(附答案)
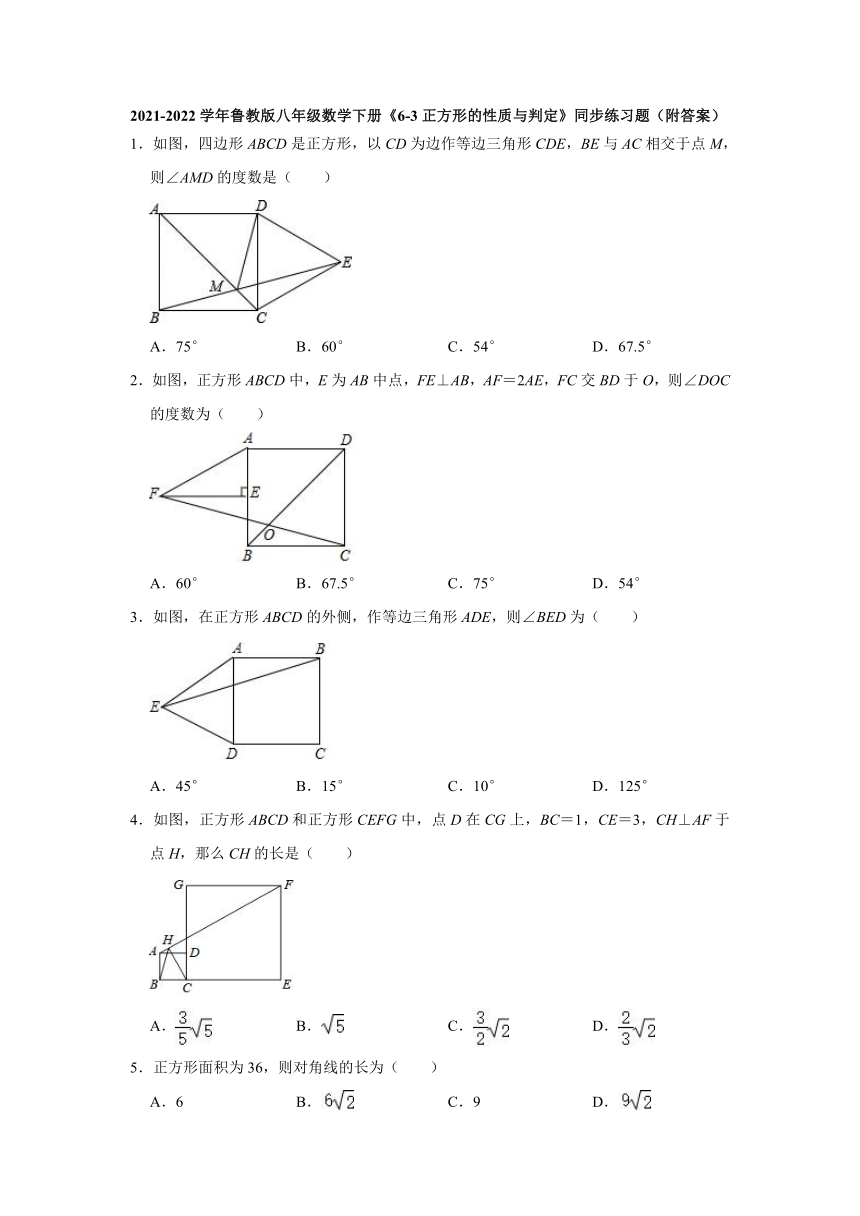
1.如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是( )
A.75° B.60° C.54° D.67.5°
2.如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )
A.60° B.67.5° C.75° D.54°
3.如图,在正方形ABCD的外侧,作等边三角形ADE,则∠BED为( )
A.45° B.15° C.10° D.125°
4.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,CH⊥AF于点H,那么CH的长是( )
A. B. C. D.
5.正方形面积为36,则对角线的长为( )
A.6 B. C.9 D.
6.如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,正确结论的个数为( )
A.4个 B.3个 C.2个 D.1个
7.如图,在平面直角坐标系xOy,四边形OABC为正方形,若点B(1,3),则点C的坐标为( )
A.(﹣1,2) B.(﹣1,) C.(﹣,2) D.(﹣1,)
8.如图,在正方形ABCD中,AB=3,点EF分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为( )
A.7 B.3+ C.8 D.3+
9.如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,则∠AEB的度数为( )
A.10° B.15° C.20° D.12.5°
10.将5个边长为2cm的正方形按如图所示摆放,点A1,A2,A3,A4是正方形的中心,则这个正方形重叠部分的面积和为( )
A.2cm2 B.1cm2 C.4cm2 D.6cm2
11.正方形具有而矩形不一定有的性质是( )
A.四个角都是直角 B.对角线互相平分
C.对角线互相垂直 D.对角线相等
12.如图,已知正方形ABCD的对角线交于O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的值是( )
A.7 B.5 C.4 D.3
13.正方形、矩形、菱形都具有的特征是( )
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.对角线平分一组对角
14.下列说法正确的是( )
A.对角线互相垂直平分的四边形是正方形 B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形 D.对角线互相平分的四边形是平行四边形
15.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥DC于点F,连接EF,给出下列四个结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC,其中正确的是( )
A.l个 B.2个 C.3个 D.4个
16.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是正方形
17.顺次连接一个四边形的各边中点,得到了一个正方形,则这个四边形最可能是( )
A.平行四边形 B.菱形 C.矩形 D.正方形
18.如图,已知四边形ABCD为正方形,AB=4,点E为对角线AC上一动点,连接DE、过点E作EF⊥DE.交BC点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
19.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2,求正方形ADCE周长.
20.在△ABC中,∠BAC=90°,AD是BC边上的中线,点E为AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AD=AF;
(2)填空:①当∠ACB= °时,四边形ADCF为正方形;
②连接DF,当∠ACB= °时,四边形ABDF为菱形.
21.如图,正方形ABCD的对角线AC与BD交于点O,分别过点C、点D作CE∥BD,DE∥AC.求证:四边形OCED是正方形.
22.如图①,在正方形ABCD中,点E,F分别在AB、BC上,且AE=BF.
(1)试探索线段AF、DE的数量关系,写出你的结论并说明理由;
(2)连接EF、DF,分别取AE、EF、FD、DA的中点H、I、J、K,则四边形HIJK是什么特殊平行四边形?请在图②中补全图形,并说明理由.
参考答案
1.解:如图,连接BD,
∵∠BCE=∠BCD+∠DCE=90°+60°=150°,BC=EC,
∴∠EBC=∠BEC=(180°﹣∠BCE)=15°
∵∠BCM=∠BCD=45°,
∴∠BMC=180°﹣(∠BCM+∠EBC)=120°,
∴∠AMB=180°﹣∠BMC=60°
∵AC是线段BD的垂直平分线,M在AC上,
∴∠AMD=∠AMB=60°
故选:B.
2.解:如图,连接DF、BF.
∵FE⊥AB,AE=EB,
∴FA=FB,
∵AF=2AE,
∴AF=AB=FB,
∴△AFB是等边三角形,
∵AF=AD=AB,
∴点A是△DBF的外接圆的圆心,
∴∠FDB=∠FAB=30°,
∵四边形ABCD是正方形,
∴AD=BC,∠DAB=∠ABC=90°,∠ADB=∠DBC=45°,
∴∠FAD=∠FBC,
∴△FAD≌△FBC,
∴∠ADF=∠FCB=15°,
∴∠DOC=∠OBC+∠OCB=60°.
解法二:连接BF.易知∠FCB=15°,∠DOC=∠OBC+∠FCB=45°+15°=60°
故选:A.
3.解:∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE=DE,
∵四边形ABCD是正方形,
∴∠BAD=90°,AD=AB
∴∠BAE=90°+60°=150°,AE=AB
∴∠AEB=30°÷2=15°,
∴∠BED=60°﹣15°=45°,
故选:A.
4.解:∵CD=BC=1,
∴GD=3﹣1=2,
∴DK=DG,
∴DK=2×=,GK=2×=,
∴KF=,
∴CH=.
方法二:连接AC、CF,利用面积法:CH=;
故选:A.
5.解:设对角线长是x.则有
x2=36,
解得:x=6.
故选:B.
6.解:在正方形ABCD中,∠BAF=∠D=90°,AB=AD=CD,
∵CE=DF,
∴AD﹣DF=CD﹣CE,
即AF=DE,
在△ABF和△DAE中,,
∴△ABF≌△DAE(SAS),
∴AE=BF,故①正确;
∠ABF=∠DAE,
∵∠DAE+∠BAO=90°,
∴∠ABF+∠BAO=90°,
在△ABO中,∠AOB=180°﹣(∠ABF+∠BAO)=180°﹣90°=90°,
∴AE⊥BF,故②正确;
假设AO=OE,
∵AE⊥BF(已证),
∴AB=BE(线段垂直平分线上的点到线段两端点的距离相等),
∵在Rt△BCE中,BE>BC,
∴AB>BC,这与正方形的边长AB=BC相矛盾,
所以,假设不成立,AO≠OE,故③错误;∵△ABF≌△DAE,
∴S△ABF=S△DAE,
∴S△ABF﹣S△AOF=S△DAE﹣S△AOF,
即S△AOB=S四边形DEOF,故④正确;
综上所述,错误的有③.
故选:B.
7.解:作CD⊥x轴于D,作BE⊥CD于E,交y轴于F,如图,
∵B(1,3),
∴DE=3,BF=1,
设C(m,n),则OD=EF=﹣m,CD=n,
∵四边形ABCO为正方形,
∴∠BCO=90°,CB=CO,
∵∠BCE+∠OCD=90°,∠BCE+∠CBE=90°,
∴∠OCD=∠CBE,
在△OCD和△CBE中
,
∴△OCD≌△CBE(AAS),
∴CD=BE,OD=CE,
即n=1﹣m,﹣m=3﹣n,
∴m=﹣1,n=2,
∴C点坐标为(﹣1,2).
故选:A.
8.解:∵阴影部分的面积与正方形ABCD的面积之比为2:3,
∴阴影部分的面积为×9=6,
∴空白部分的面积为9﹣6=3,
由CE=DF,BC=CD,∠BCE=∠CDF=90°,可得△BCE≌△CDF,
∴△BCG的面积与四边形DEGF的面积相等,均为×3=,
∠CBE=∠DCF,
∵∠DCF+∠BCG=90°,
∴∠CBG+∠BCG=90°,即∠BGC=90°,
设BG=a,CG=b,则ab=,
又∵a2+b2=32,
∴a2+2ab+b2=9+6=15,
即(a+b)2=15,
∴a+b=,即BG+CG=,
∴△BCG的周长=+3,
故选:D.
9.解:根据等边三角形和正方形的性质可知AB=AE,
∴∠BAE=90°+60°=150°,
∴∠AEB=(180°﹣150°)÷2=15°.
故选:B.
10.解:如图,
在正方形ABCD中,作A1E⊥AD,A1F⊥DC,
两边相交于M和N,
∠A1EN=∠A1MF=90°,
∠EA1N+∠ENA1=90°,
∠EA1N+∠FA1M=90°,
∴∠ENA1=∠FA1M,A1E=A1F,
∴△A1EN≌△A1MF(ASA),
∴四边形A1MA2N的面积=四边形EA1FA2的面积=正方形ABCD的面积,
同理可证,另外三个阴影四边形的面积都等于正方形ABCD的面积,
∴图中重叠部分(阴影部分)的面积和=正方形ABCD的面积=4cm2,
故选:C.
11.解:A、正方形和矩形的四个角都是直角,故本选项不符合题意;
B、正方形和矩形的对角线互相平分,故本选项不符合题意;
C、正方形的对角线互相垂直,矩形的对角线不互相垂直,故本选项符合题意.
D、正方形和矩形的对角线都相等,故本选项不符合题意;
故选:C.
12.解:∵OB=OC,
∵OE⊥OF
∴∠EOB+∠FOB=90°
∵四边形ABCD是正方形
∴∠COF+∠BOF=90°
∴∠EOB=∠FOC
而∠OBE=∠OCF=45°
在△OFC和△OEB中,
∴△OFC≌△OEB(ASA),
∴OE=OF,CF=BE=3cm,则AE=BF=4,
根据勾股定理得到EF==5cm.
故选:B.
13.解:A、三者均具有此性质,故正确;
B、菱形不具有此性质,故不正确;
C、矩形不具有此性质,故不正确;
D、矩形不具有此性质,故不正确;
故选:A.
14.解:(A)对角线互相垂直平分的四边形是菱形,故A错误.
(B)对角线相等且互相平分的四边形是矩形,故B错误.
(C)对角线互相垂直且平分的四边形是菱形,故C错误.
故选:D.
15.解:过P作PG⊥AB于点G,如图,
∵点P是正方形ABCD的对角线BD上一点,
∴GP=EP,
在△GPB中,∠GBP=45°,
∴∠GPB=45°,
∴GB=GP,
同理,得
PE=BE,
∵AB=BC=GF,
∴AG=AB﹣GB,FP=GF﹣GP=AB﹣GB,
∴AG=PF,
∴△AGP≌△FPE(SAS),
∴AP=EF,
∴结论①正确;
∵△AGP≌△FPE,
∴∠PFE=∠GAP
∴∠PFE=∠BAP,
∴结论③正确;
②延长AP到EF上于一点H,
∴∠PAG=∠PFH,
∵∠APG=∠FPH,
∴∠PHF=∠PGA=90°,
即AP⊥EF;
∴结论②正确;
∵GF∥BC,
∴∠DPF=∠DBC,
又∵∠DPF=∠DBC=45°,
∴∠PDF=∠DPF=45°,
∴PF=EC,
在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,
∴PD=EC,
∴结论④正确;
故选:D.
16.解:A、根据邻边相等的平行四边形是菱形可知:四边形ABCD是平行四边形,当AB=BC时,它是菱形,故A选项正确;
B、∵四边形ABCD是平行四边形,AC⊥BD,∴四边形ABCD是菱形,故B选项正确;
C、有一个角是直角的平行四边形是矩形,故C选项正确;
D、根据对角线相等的平行四边形是矩形可知当AC=BD时,它是矩形,不是正方形,故D选项错误;
综上所述,符合题意是D选项;
故选:D.
17.解:如图,∵点E,F,G,H分别是四边形ABCD各边的中点,且四边形EFGH是正方形,
∴EF=EH,EF⊥EH,
∵BD=2EF,AC=2EH,
∴AC=BD,AC⊥BD,
即四边形ABCD满足对角线相等且垂直,
选项D满足题意.
故选:D.
18.解:(1)如图所示,过E作EM⊥BC于M点,过E作EN⊥CD于N点,
∵正方形ABCD,
∴∠BCD=90°,∠ECN=45°,
∴∠EMC=∠ENC=∠BCD=90°,且NE=NC,
∴四边形EMCN为正方形,
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°,
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中,,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形
(2)CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°,
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴AC=AE+CE=AB=×4=8,
∴CE+CG=8是定值.
19.(1)证明:∵AB=AC,AD⊥BC,垂足为点D,
∴∠CAD=∠BAC.
∵AN是△ABC外角∠CAM的平分线,
∴∠CAE=∠CAM.
∵∠BAC与∠CAM是邻补角,
∴∠BAC+∠CAM=180°,
∴∠CAD+∠CAE=(∠BAC+∠CAM)=90°.
∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形;
(2)∠BAC=90°且AB=AC时,四边形ADCE是一个正方形,
证明:∵∠BAC=90°且AB=AC,AD⊥BC,
∴∠CAD=∠BAC=45°,∠ADC=90°,
∴∠ACD=∠CAD=45°,
∴AD=CD.
∵四边形ADCE为矩形,
∴四边形ADCE为正方形;
(3)解:由勾股定理,得
=AB,AD=CD,
即AD=2,
AD=2,
正方形ADCE周长4AD=4×2=8.
20.(1)证明:∵∠BAC=90°,AD是BC边上的中线,
∵AD=CD=BD,
∵点E为AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
∵∠AEF=∠DEB,
∴△AEF≌△DEB(AAS),
∴AF=BD,
∴AD=AF;
(2)解:①∵AF∥CD,AF=CD,AD=AF,
∴四边形ADCF是菱形,
当四边形ADCF为正方形时,∠DCF=90°,
∴∠ACB=∠ACF=45°;
②∴CD=CF,
当四边形ABCF为菱形时,BD=DF,则DC=DF,
∴CD=CF=DF,
∴△DCF为等边三角形,
∴∠DCF=60°,
∴∠ACB=∠ACF=30°.
故答案为:45,30.
21.证明:∵CE∥BD,DE∥AC,
∴四边形OCED是平行四边形,
∵四边形ABCD是正方形,
∴OA=OC=OB=OD,AC⊥BD,
∴四边形OCED是正方形.
22.解:(1)AF=DE.
∵ABCD是正方形,
∴AB=AD,∠DAB=∠ABC=90°,
∵AE=BF,
∴△DAE≌△ABF,
∴AF=DE.
(2)四边形HIJK是正方形.
如下图,H、I、J、K分别是AE、EF、FD、DA的中点,
∴HI=KJ=AF,HK=IJ=ED,
∵AF=DE,
∴HI=KJ=HK=IJ,
∴四边形HIJK是菱形,
∵△DAE≌△ABF,
∴∠ADE=∠BAF,
∵∠ADE+∠AED=90°,
∴∠BAF+∠AED=90°,
∴∠AOE=90°
∴∠KHI=90°,
∴四边形HIJK是正方形.
1.如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是( )
A.75° B.60° C.54° D.67.5°
2.如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )
A.60° B.67.5° C.75° D.54°
3.如图,在正方形ABCD的外侧,作等边三角形ADE,则∠BED为( )
A.45° B.15° C.10° D.125°
4.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,CH⊥AF于点H,那么CH的长是( )
A. B. C. D.
5.正方形面积为36,则对角线的长为( )
A.6 B. C.9 D.
6.如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,正确结论的个数为( )
A.4个 B.3个 C.2个 D.1个
7.如图,在平面直角坐标系xOy,四边形OABC为正方形,若点B(1,3),则点C的坐标为( )
A.(﹣1,2) B.(﹣1,) C.(﹣,2) D.(﹣1,)
8.如图,在正方形ABCD中,AB=3,点EF分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为( )
A.7 B.3+ C.8 D.3+
9.如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,则∠AEB的度数为( )
A.10° B.15° C.20° D.12.5°
10.将5个边长为2cm的正方形按如图所示摆放,点A1,A2,A3,A4是正方形的中心,则这个正方形重叠部分的面积和为( )
A.2cm2 B.1cm2 C.4cm2 D.6cm2
11.正方形具有而矩形不一定有的性质是( )
A.四个角都是直角 B.对角线互相平分
C.对角线互相垂直 D.对角线相等
12.如图,已知正方形ABCD的对角线交于O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的值是( )
A.7 B.5 C.4 D.3
13.正方形、矩形、菱形都具有的特征是( )
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.对角线平分一组对角
14.下列说法正确的是( )
A.对角线互相垂直平分的四边形是正方形 B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形 D.对角线互相平分的四边形是平行四边形
15.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥DC于点F,连接EF,给出下列四个结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC,其中正确的是( )
A.l个 B.2个 C.3个 D.4个
16.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是正方形
17.顺次连接一个四边形的各边中点,得到了一个正方形,则这个四边形最可能是( )
A.平行四边形 B.菱形 C.矩形 D.正方形
18.如图,已知四边形ABCD为正方形,AB=4,点E为对角线AC上一动点,连接DE、过点E作EF⊥DE.交BC点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
19.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2,求正方形ADCE周长.
20.在△ABC中,∠BAC=90°,AD是BC边上的中线,点E为AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AD=AF;
(2)填空:①当∠ACB= °时,四边形ADCF为正方形;
②连接DF,当∠ACB= °时,四边形ABDF为菱形.
21.如图,正方形ABCD的对角线AC与BD交于点O,分别过点C、点D作CE∥BD,DE∥AC.求证:四边形OCED是正方形.
22.如图①,在正方形ABCD中,点E,F分别在AB、BC上,且AE=BF.
(1)试探索线段AF、DE的数量关系,写出你的结论并说明理由;
(2)连接EF、DF,分别取AE、EF、FD、DA的中点H、I、J、K,则四边形HIJK是什么特殊平行四边形?请在图②中补全图形,并说明理由.
参考答案
1.解:如图,连接BD,
∵∠BCE=∠BCD+∠DCE=90°+60°=150°,BC=EC,
∴∠EBC=∠BEC=(180°﹣∠BCE)=15°
∵∠BCM=∠BCD=45°,
∴∠BMC=180°﹣(∠BCM+∠EBC)=120°,
∴∠AMB=180°﹣∠BMC=60°
∵AC是线段BD的垂直平分线,M在AC上,
∴∠AMD=∠AMB=60°
故选:B.
2.解:如图,连接DF、BF.
∵FE⊥AB,AE=EB,
∴FA=FB,
∵AF=2AE,
∴AF=AB=FB,
∴△AFB是等边三角形,
∵AF=AD=AB,
∴点A是△DBF的外接圆的圆心,
∴∠FDB=∠FAB=30°,
∵四边形ABCD是正方形,
∴AD=BC,∠DAB=∠ABC=90°,∠ADB=∠DBC=45°,
∴∠FAD=∠FBC,
∴△FAD≌△FBC,
∴∠ADF=∠FCB=15°,
∴∠DOC=∠OBC+∠OCB=60°.
解法二:连接BF.易知∠FCB=15°,∠DOC=∠OBC+∠FCB=45°+15°=60°
故选:A.
3.解:∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE=DE,
∵四边形ABCD是正方形,
∴∠BAD=90°,AD=AB
∴∠BAE=90°+60°=150°,AE=AB
∴∠AEB=30°÷2=15°,
∴∠BED=60°﹣15°=45°,
故选:A.
4.解:∵CD=BC=1,
∴GD=3﹣1=2,
∴DK=DG,
∴DK=2×=,GK=2×=,
∴KF=,
∴CH=.
方法二:连接AC、CF,利用面积法:CH=;
故选:A.
5.解:设对角线长是x.则有
x2=36,
解得:x=6.
故选:B.
6.解:在正方形ABCD中,∠BAF=∠D=90°,AB=AD=CD,
∵CE=DF,
∴AD﹣DF=CD﹣CE,
即AF=DE,
在△ABF和△DAE中,,
∴△ABF≌△DAE(SAS),
∴AE=BF,故①正确;
∠ABF=∠DAE,
∵∠DAE+∠BAO=90°,
∴∠ABF+∠BAO=90°,
在△ABO中,∠AOB=180°﹣(∠ABF+∠BAO)=180°﹣90°=90°,
∴AE⊥BF,故②正确;
假设AO=OE,
∵AE⊥BF(已证),
∴AB=BE(线段垂直平分线上的点到线段两端点的距离相等),
∵在Rt△BCE中,BE>BC,
∴AB>BC,这与正方形的边长AB=BC相矛盾,
所以,假设不成立,AO≠OE,故③错误;∵△ABF≌△DAE,
∴S△ABF=S△DAE,
∴S△ABF﹣S△AOF=S△DAE﹣S△AOF,
即S△AOB=S四边形DEOF,故④正确;
综上所述,错误的有③.
故选:B.
7.解:作CD⊥x轴于D,作BE⊥CD于E,交y轴于F,如图,
∵B(1,3),
∴DE=3,BF=1,
设C(m,n),则OD=EF=﹣m,CD=n,
∵四边形ABCO为正方形,
∴∠BCO=90°,CB=CO,
∵∠BCE+∠OCD=90°,∠BCE+∠CBE=90°,
∴∠OCD=∠CBE,
在△OCD和△CBE中
,
∴△OCD≌△CBE(AAS),
∴CD=BE,OD=CE,
即n=1﹣m,﹣m=3﹣n,
∴m=﹣1,n=2,
∴C点坐标为(﹣1,2).
故选:A.
8.解:∵阴影部分的面积与正方形ABCD的面积之比为2:3,
∴阴影部分的面积为×9=6,
∴空白部分的面积为9﹣6=3,
由CE=DF,BC=CD,∠BCE=∠CDF=90°,可得△BCE≌△CDF,
∴△BCG的面积与四边形DEGF的面积相等,均为×3=,
∠CBE=∠DCF,
∵∠DCF+∠BCG=90°,
∴∠CBG+∠BCG=90°,即∠BGC=90°,
设BG=a,CG=b,则ab=,
又∵a2+b2=32,
∴a2+2ab+b2=9+6=15,
即(a+b)2=15,
∴a+b=,即BG+CG=,
∴△BCG的周长=+3,
故选:D.
9.解:根据等边三角形和正方形的性质可知AB=AE,
∴∠BAE=90°+60°=150°,
∴∠AEB=(180°﹣150°)÷2=15°.
故选:B.
10.解:如图,
在正方形ABCD中,作A1E⊥AD,A1F⊥DC,
两边相交于M和N,
∠A1EN=∠A1MF=90°,
∠EA1N+∠ENA1=90°,
∠EA1N+∠FA1M=90°,
∴∠ENA1=∠FA1M,A1E=A1F,
∴△A1EN≌△A1MF(ASA),
∴四边形A1MA2N的面积=四边形EA1FA2的面积=正方形ABCD的面积,
同理可证,另外三个阴影四边形的面积都等于正方形ABCD的面积,
∴图中重叠部分(阴影部分)的面积和=正方形ABCD的面积=4cm2,
故选:C.
11.解:A、正方形和矩形的四个角都是直角,故本选项不符合题意;
B、正方形和矩形的对角线互相平分,故本选项不符合题意;
C、正方形的对角线互相垂直,矩形的对角线不互相垂直,故本选项符合题意.
D、正方形和矩形的对角线都相等,故本选项不符合题意;
故选:C.
12.解:∵OB=OC,
∵OE⊥OF
∴∠EOB+∠FOB=90°
∵四边形ABCD是正方形
∴∠COF+∠BOF=90°
∴∠EOB=∠FOC
而∠OBE=∠OCF=45°
在△OFC和△OEB中,
∴△OFC≌△OEB(ASA),
∴OE=OF,CF=BE=3cm,则AE=BF=4,
根据勾股定理得到EF==5cm.
故选:B.
13.解:A、三者均具有此性质,故正确;
B、菱形不具有此性质,故不正确;
C、矩形不具有此性质,故不正确;
D、矩形不具有此性质,故不正确;
故选:A.
14.解:(A)对角线互相垂直平分的四边形是菱形,故A错误.
(B)对角线相等且互相平分的四边形是矩形,故B错误.
(C)对角线互相垂直且平分的四边形是菱形,故C错误.
故选:D.
15.解:过P作PG⊥AB于点G,如图,
∵点P是正方形ABCD的对角线BD上一点,
∴GP=EP,
在△GPB中,∠GBP=45°,
∴∠GPB=45°,
∴GB=GP,
同理,得
PE=BE,
∵AB=BC=GF,
∴AG=AB﹣GB,FP=GF﹣GP=AB﹣GB,
∴AG=PF,
∴△AGP≌△FPE(SAS),
∴AP=EF,
∴结论①正确;
∵△AGP≌△FPE,
∴∠PFE=∠GAP
∴∠PFE=∠BAP,
∴结论③正确;
②延长AP到EF上于一点H,
∴∠PAG=∠PFH,
∵∠APG=∠FPH,
∴∠PHF=∠PGA=90°,
即AP⊥EF;
∴结论②正确;
∵GF∥BC,
∴∠DPF=∠DBC,
又∵∠DPF=∠DBC=45°,
∴∠PDF=∠DPF=45°,
∴PF=EC,
在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,
∴PD=EC,
∴结论④正确;
故选:D.
16.解:A、根据邻边相等的平行四边形是菱形可知:四边形ABCD是平行四边形,当AB=BC时,它是菱形,故A选项正确;
B、∵四边形ABCD是平行四边形,AC⊥BD,∴四边形ABCD是菱形,故B选项正确;
C、有一个角是直角的平行四边形是矩形,故C选项正确;
D、根据对角线相等的平行四边形是矩形可知当AC=BD时,它是矩形,不是正方形,故D选项错误;
综上所述,符合题意是D选项;
故选:D.
17.解:如图,∵点E,F,G,H分别是四边形ABCD各边的中点,且四边形EFGH是正方形,
∴EF=EH,EF⊥EH,
∵BD=2EF,AC=2EH,
∴AC=BD,AC⊥BD,
即四边形ABCD满足对角线相等且垂直,
选项D满足题意.
故选:D.
18.解:(1)如图所示,过E作EM⊥BC于M点,过E作EN⊥CD于N点,
∵正方形ABCD,
∴∠BCD=90°,∠ECN=45°,
∴∠EMC=∠ENC=∠BCD=90°,且NE=NC,
∴四边形EMCN为正方形,
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°,
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中,,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形
(2)CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°,
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴AC=AE+CE=AB=×4=8,
∴CE+CG=8是定值.
19.(1)证明:∵AB=AC,AD⊥BC,垂足为点D,
∴∠CAD=∠BAC.
∵AN是△ABC外角∠CAM的平分线,
∴∠CAE=∠CAM.
∵∠BAC与∠CAM是邻补角,
∴∠BAC+∠CAM=180°,
∴∠CAD+∠CAE=(∠BAC+∠CAM)=90°.
∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形;
(2)∠BAC=90°且AB=AC时,四边形ADCE是一个正方形,
证明:∵∠BAC=90°且AB=AC,AD⊥BC,
∴∠CAD=∠BAC=45°,∠ADC=90°,
∴∠ACD=∠CAD=45°,
∴AD=CD.
∵四边形ADCE为矩形,
∴四边形ADCE为正方形;
(3)解:由勾股定理,得
=AB,AD=CD,
即AD=2,
AD=2,
正方形ADCE周长4AD=4×2=8.
20.(1)证明:∵∠BAC=90°,AD是BC边上的中线,
∵AD=CD=BD,
∵点E为AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
∵∠AEF=∠DEB,
∴△AEF≌△DEB(AAS),
∴AF=BD,
∴AD=AF;
(2)解:①∵AF∥CD,AF=CD,AD=AF,
∴四边形ADCF是菱形,
当四边形ADCF为正方形时,∠DCF=90°,
∴∠ACB=∠ACF=45°;
②∴CD=CF,
当四边形ABCF为菱形时,BD=DF,则DC=DF,
∴CD=CF=DF,
∴△DCF为等边三角形,
∴∠DCF=60°,
∴∠ACB=∠ACF=30°.
故答案为:45,30.
21.证明:∵CE∥BD,DE∥AC,
∴四边形OCED是平行四边形,
∵四边形ABCD是正方形,
∴OA=OC=OB=OD,AC⊥BD,
∴四边形OCED是正方形.
22.解:(1)AF=DE.
∵ABCD是正方形,
∴AB=AD,∠DAB=∠ABC=90°,
∵AE=BF,
∴△DAE≌△ABF,
∴AF=DE.
(2)四边形HIJK是正方形.
如下图,H、I、J、K分别是AE、EF、FD、DA的中点,
∴HI=KJ=AF,HK=IJ=ED,
∵AF=DE,
∴HI=KJ=HK=IJ,
∴四边形HIJK是菱形,
∵△DAE≌△ABF,
∴∠ADE=∠BAF,
∵∠ADE+∠AED=90°,
∴∠BAF+∠AED=90°,
∴∠AOE=90°
∴∠KHI=90°,
∴四边形HIJK是正方形.
