2021-2022学年北师大版九年级数学下册3.5确定圆的条件 同步达标测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.5确定圆的条件 同步达标测试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 153.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 19:25:42 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《3-5确定圆的条件》同步达标测试题(附答案)
一.选择题(共10小题,满分50分)
1.下列说法正确的是( )
A.经过三点可以作一个圆
B.三角形的外心是三个内角平分线的交点
C.相等的圆心角所对的弧相等
D.等弧所对的圆心角相等
2.已知点P在半径为8的⊙O外,则( )
A.OP>8 B.OP=8 C.OP<8 D.OP≠8
3.下列说法正确的是( )
A.过一点A的圆的圆心可以是平面上任意点
B.同一平面内,过两点A、B的圆的圆心在一条直线上
C.过三点A、B、C的圆的圆心有且只有一点
D.过四点A、B、C、D的圆不存在
4.下列语句中,一定正确的是( )
①过三点有且只有一个圆;②平分弦的直径垂直于弦;③三角形的外心到三角形三个顶点的距离相等;④同弧或等弧所对的圆周角相等;⑤圆内接平行四边形是矩形.
A.①②③ B.①②④ C.②③⑤ D.③④⑤
5.如图,△ABC是⊙O的内接三角形,若∠ABC=60°,则∠AOC的大小是( )
A.30° B.120° C.135° D.150°
6.下列关于三角形外心的说法中,正确的是( )
A.三角形的外心是三角形各角平分线的交点
B.三角形的外心是三角形三边中线的交点
C.三角形的外心是三角形三边高线的交点
D.三角形的外心是三角形三边垂直平分线的交点
7.如图,在矩形ABCD中,点E是AB的中点,点F是BC的中点,连接EF,G是EF的中点,连接DG.在△BEF中,BE=2,∠BFE=30°,若将△BEF绕点B逆时针旋转,则在旋转的过程中,线段DG长的最大值是( )
A. B. C.10 D.12
8.如图,△ABC是⊙O的内接三角形,∠AOB=60°,AB=AC=2,则弦BC的长为( )
A.4 B. C.2 D.
9.有下列说法:①半径是弦;②任意一个三角形有且只有一个外接圆;③平分弦的直径垂直于弦;④半圆所对的圆周角是90°;⑤相等的圆周角所对的弧相等,其中正确的个数有( )
A.2个 B.3个 C.4个 D.5个
10.如图,△ABC为等边三角形,AB=3.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为( )
A.1.5 B. C. D.2
二.填空题(共6小题,满分30分)
11.一个直角三角形的两条边长是方程x2﹣7x+12=0的两个根,则此直角三角形的外接圆的直径为 .
12.直角三角形的两条直角边为6、8,则外接圆的半径为 .
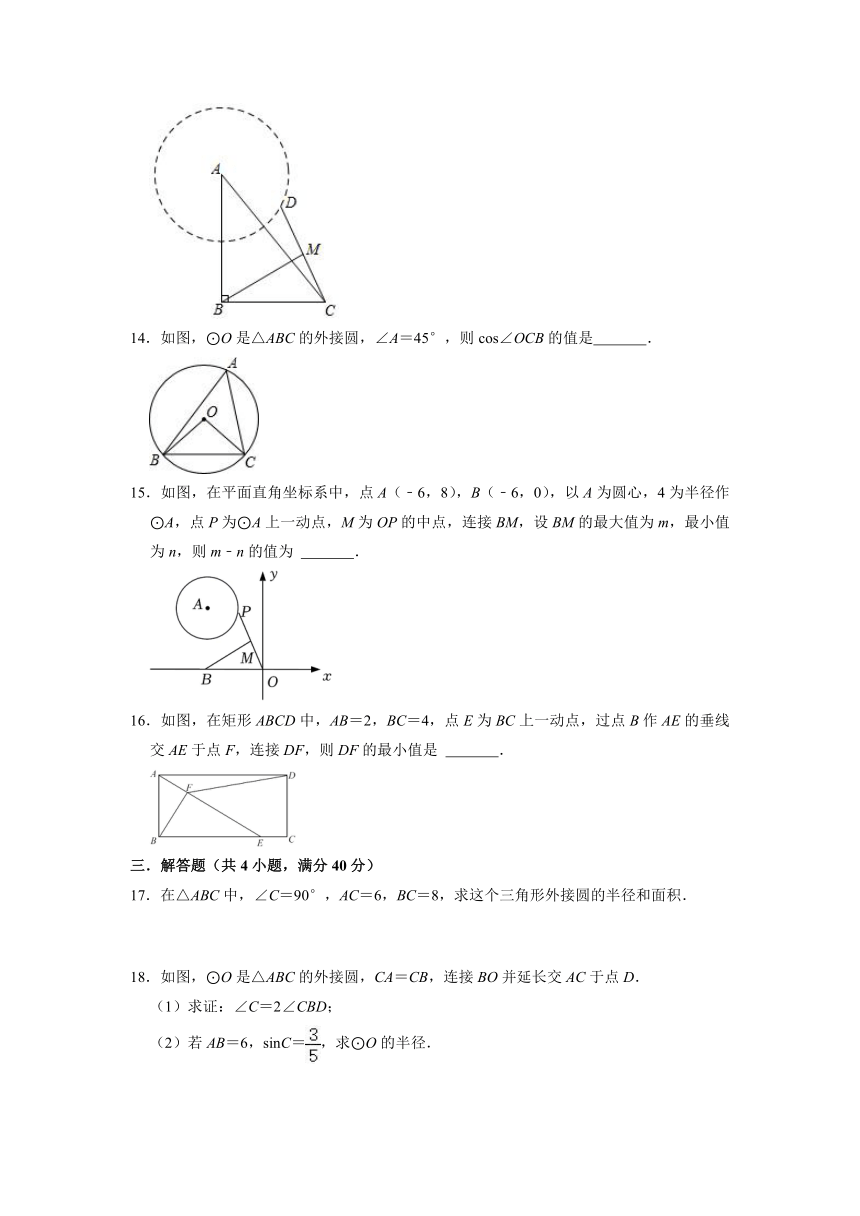
13.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D是半径为4的⊙A上一动点,点M是CD的中点,则BM的最大值是 .
14.如图,⊙O是△ABC的外接圆,∠A=45°,则cos∠OCB的值是 .
15.如图,在平面直角坐标系中,点A(﹣6,8),B(﹣6,0),以A为圆心,4为半径作⊙A,点P为⊙A上一动点,M为OP的中点,连接BM,设BM的最大值为m,最小值为n,则m﹣n的值为 .
16.如图,在矩形ABCD中,AB=2,BC=4,点E为BC上一动点,过点B作AE的垂线交AE于点F,连接DF,则DF的最小值是 .
三.解答题(共4小题,满分40分)
17.在△ABC中,∠C=90°,AC=6,BC=8,求这个三角形外接圆的半径和面积.
18.如图,⊙O是△ABC的外接圆,CA=CB,连接BO并延长交AC于点D.
(1)求证:∠C=2∠CBD;
(2)若AB=6,sinC=,求⊙O的半径.
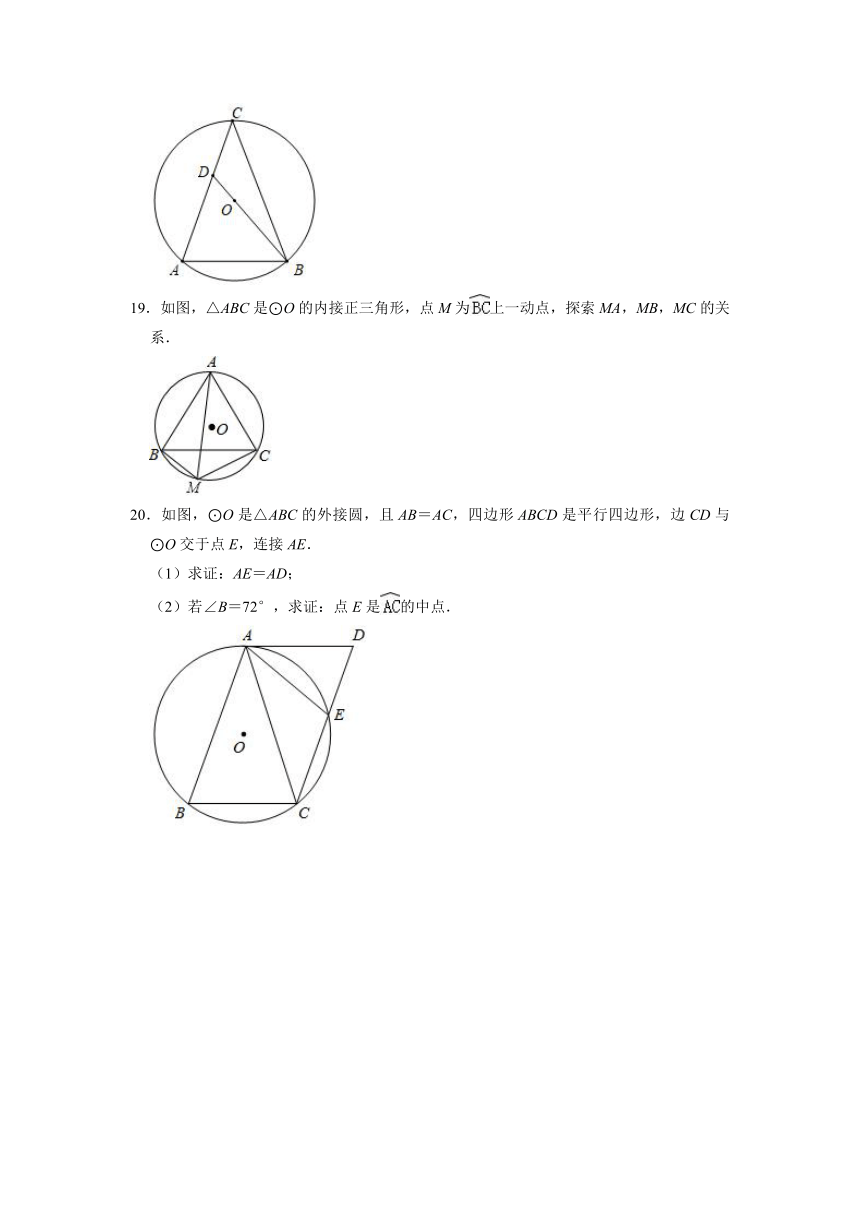
19.如图,△ABC是⊙O的内接正三角形,点M为上一动点,探索MA,MB,MC的关系.
20.如图,⊙O是△ABC的外接圆,且AB=AC,四边形ABCD是平行四边形,边CD与⊙O交于点E,连接AE.
(1)求证:AE=AD;
(2)若∠B=72°,求证:点E是的中点.
参考答案
一.选择题(共10小题,满分50分)
1.解:A、经过不共线的三点可以作一个圆,所以A选项的说法错误;
B、三角形的外心到三个顶点的距离相等,所以B选项的说法错误;
C、在同圆或等圆中,相等的圆心角所对的弧相等,所以选项C说法错误;
D、等弧所对的圆心角相等,所以D选项的说法正确;
故选:D.
2.解:∵点P在圆O的外部,
∴点P到圆心O的距离大于8,
故选:A.
3.解:A、过一点A的圆的圆心可以是平面上任意点(A点外),故本选项错误,
B、在同一平面内,过两点A、B的圆的圆心在线段AB的垂直平分线上,故正确,
C、错误,A、B、C三点共线时,不符合题意.
D、过四点A、B、C、D的圆可以存在,故本选项错误,
故选:B.
4.解:过不在同一直线上的三点有且只有一个圆,所以①错误;
平分弦(非直径)的直径垂直于弦,所以②错误;
三角形的外心到三角形三个顶点的距离相等,所以③正确;
同弧或等弧所对的圆周角相等,所以④正确;
圆内接平行四边形的对角相等且互补,此时四边形是矩形,所以⑤正确.
故选:D.
5.解:∵∠AOC和∠ABC是同弧所对的圆心角和圆周角,
∴∠AOC=2∠ABC=120°;
故选:B.
6.解:∵三角形的外心是三角形三边垂直平分线的交点,
∴A、B、C选项错误,D选项正确,
故选:D.
7.解:连接BG,
在△BEF中,BE=2,∠BFE=30°,
∴EF=2BE=4,BF=BE=2,
∵G是EF的中点,
∴BG=EF=2,
∴G在⊙B上,且半径为2,
∴当G在DB的延长线上时,DG最大,
∵BE=2,BF=2,点E是AB的中点,点F是BC的中点,
∴AB=4,BC=4,
∴BD==8,
∴DG的最大值为8+2=10,
故选:C.
8.解:如图,设AO与BC交于点D,
∵∠AOB=60°,
∴∠C=∠AOB=30°,
∵AB=AC,
∴=,
∴AD⊥BC,
∴BD=CD,
在Rt△ACD中,CD=AC cos30°=2×=,
∴BC=2CD=2,
故选:D.
9.解:①半径不是弦,本小题说法是假命题;
②任意三角形都有且只有一个外接圆,本小题说法是真命题;
③平分弦(不是直径)的直径垂直于这条弦,本小题说法是假命题;
④半圆所对的圆周角是90°,本小题说法是真命题;
⑤在同圆或等圆中,相等的圆周角所对的弧相等,本小题说法是假命题;
故选:A.
10.解:∵△ABC是等边三角形,
∴∠ABC=∠BAC=60°,AC=AB=3,
∵∠PAB=∠ACP,
∴∠PAC+∠ACP=60°,
∴∠APC=120°,
∴点P的运动轨迹是,
设所在圆的圆心为O,当O、P、B共线时,PB长度最小,设OB交AC于D,如图所示:
此时PA=PC,OB⊥AC,
则AD=CD=AC=,∠PAC=∠ACP=30°,∠ABD=∠ABC=30°,
∴PD=,BD=,
∴PB=BD﹣PD=﹣=.
故选:B.
二.填空题(共6小题,满分30分)
11.解:x2﹣7x+12=0,
(x﹣3)(x﹣4)=0,
解得:x1=3,x2=4,
①当直角边分别为3,4时,
斜边为:=5,
此时直角三角形外接圆的直径为5,
②当直角边为3,斜边为4时,
此时直角三角形外接圆直径为4.
故答案为4或5.
12.解:∵直角边长分别为6和8,
∴斜边是10,
∴这个直角三角形的外接圆的半径为5,
故答案为:5.
13.解:如图,取AC的中点N,连接MN,BN.
∵∠ABC=90°,AB=8,BC=6,
∴AC=10,
∵AN=NC,
∴BN=AC=5,
∵AN=NC,DM=MC,
∴MN==2,
∴BM≤BN+NM,
∴BM≤5+2=7,
即BM的最大值是7.
故答案为7.
14.解:∵∠BOC=2∠A=2×45°=90°,
而OB=OC,
∴△OBC为等腰直角三角形,
∴∠OCB=45°,
∴cos∠OCB=.
故答案为.
15.解:在x轴上取一点E(﹣12,0),连接PE.
∵B(﹣6,0),A(﹣6,8),
∴OB=BE=6,AE==10,
∵OM=PM,OB=BE,
∴BM=PE,
∵点P在⊙A上运动,
∴P,A,B共线时,可以取得最大值或最小值,最大值=EP′=10+4=14,最小值EP″=10﹣4=6,
∴m=7,n=3,
∴m﹣n=4,
故答案为:4.
16.解:取AB的中点T,连接FT,DT.
∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AD=4,AT=TB=1,
∴DT===,
∵BF⊥AE,
∴∠AFB=90°,
∵AT=TB,
∴FT=AB=1,
∴DF≥DT﹣FT=﹣1,
∴DF的最小值为﹣1.
故答案为:﹣1.
三.解答题(共4小题,满分40分)
17.解:∵∠C=90°,AC=6,BC=8,
∴AB==10,
∴Rt△ABC的外接圆的半径为5,
面积为π×52=25π.
18.解:(1)如图1,连接CO,AO,
∵CA=CB,OA=OB,OC=OC,
∴△COA≌△COB(SSS),
∴∠ACO=∠BCO,
∵OC=OB,
∴∠BCO=∠CBD,
∴∠C=2∠CBD;
(2)如图2,作⊙O的直径AK,连接BK,
则∠ABK=90°,∠C=∠K,
∵AB=6,sinC=,
∴sinK==,
∴AK=10,
∴⊙O的半径为5.
19.解:MB+MC=MA.
理由如下:截取ME=MC,
∵∠AMC=∠ABC=60°,
∴△MEC为等边三角形,
∴CE=CM,∠MCE=60°,
而∠ACB=60°,
∴∠ACE=∠BCM,
在△CAE和△CBM中,
,
∴△CAE≌△CBM,
∴AE=MB,
∴MB+MC=MA.
20.证明:(1)∵四边形ABCD是平行四边形,
∴∠ABC=∠D,
∵四边形ABCE为⊙O的内接四边形,
∴∠ABC+∠AEC=180°,
∵∠AED+∠AEC=180°,
∴∠ABC=∠AED,
∴∠D=∠AED,
∴AE=AD;
(2)∵AB=AC,∠B=72°,
∴∠ABC=∠ACB=72°,∠AEC=180°﹣∠B=108°,
∴∠BAC=180°﹣72°×2=36°,
∵AB∥CD,
∴∠ACE=∠BAC=36°,
∴∠EAC=180°﹣∠AEC﹣∠ACE=36°,
∴∠ACE=∠EAC,
∴=,即点E是的中点.
一.选择题(共10小题,满分50分)
1.下列说法正确的是( )
A.经过三点可以作一个圆
B.三角形的外心是三个内角平分线的交点
C.相等的圆心角所对的弧相等
D.等弧所对的圆心角相等
2.已知点P在半径为8的⊙O外,则( )
A.OP>8 B.OP=8 C.OP<8 D.OP≠8
3.下列说法正确的是( )
A.过一点A的圆的圆心可以是平面上任意点
B.同一平面内,过两点A、B的圆的圆心在一条直线上
C.过三点A、B、C的圆的圆心有且只有一点
D.过四点A、B、C、D的圆不存在
4.下列语句中,一定正确的是( )
①过三点有且只有一个圆;②平分弦的直径垂直于弦;③三角形的外心到三角形三个顶点的距离相等;④同弧或等弧所对的圆周角相等;⑤圆内接平行四边形是矩形.
A.①②③ B.①②④ C.②③⑤ D.③④⑤
5.如图,△ABC是⊙O的内接三角形,若∠ABC=60°,则∠AOC的大小是( )
A.30° B.120° C.135° D.150°
6.下列关于三角形外心的说法中,正确的是( )
A.三角形的外心是三角形各角平分线的交点
B.三角形的外心是三角形三边中线的交点
C.三角形的外心是三角形三边高线的交点
D.三角形的外心是三角形三边垂直平分线的交点
7.如图,在矩形ABCD中,点E是AB的中点,点F是BC的中点,连接EF,G是EF的中点,连接DG.在△BEF中,BE=2,∠BFE=30°,若将△BEF绕点B逆时针旋转,则在旋转的过程中,线段DG长的最大值是( )
A. B. C.10 D.12
8.如图,△ABC是⊙O的内接三角形,∠AOB=60°,AB=AC=2,则弦BC的长为( )
A.4 B. C.2 D.
9.有下列说法:①半径是弦;②任意一个三角形有且只有一个外接圆;③平分弦的直径垂直于弦;④半圆所对的圆周角是90°;⑤相等的圆周角所对的弧相等,其中正确的个数有( )
A.2个 B.3个 C.4个 D.5个
10.如图,△ABC为等边三角形,AB=3.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为( )
A.1.5 B. C. D.2
二.填空题(共6小题,满分30分)
11.一个直角三角形的两条边长是方程x2﹣7x+12=0的两个根,则此直角三角形的外接圆的直径为 .
12.直角三角形的两条直角边为6、8,则外接圆的半径为 .
13.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D是半径为4的⊙A上一动点,点M是CD的中点,则BM的最大值是 .
14.如图,⊙O是△ABC的外接圆,∠A=45°,则cos∠OCB的值是 .
15.如图,在平面直角坐标系中,点A(﹣6,8),B(﹣6,0),以A为圆心,4为半径作⊙A,点P为⊙A上一动点,M为OP的中点,连接BM,设BM的最大值为m,最小值为n,则m﹣n的值为 .
16.如图,在矩形ABCD中,AB=2,BC=4,点E为BC上一动点,过点B作AE的垂线交AE于点F,连接DF,则DF的最小值是 .
三.解答题(共4小题,满分40分)
17.在△ABC中,∠C=90°,AC=6,BC=8,求这个三角形外接圆的半径和面积.
18.如图,⊙O是△ABC的外接圆,CA=CB,连接BO并延长交AC于点D.
(1)求证:∠C=2∠CBD;
(2)若AB=6,sinC=,求⊙O的半径.
19.如图,△ABC是⊙O的内接正三角形,点M为上一动点,探索MA,MB,MC的关系.
20.如图,⊙O是△ABC的外接圆,且AB=AC,四边形ABCD是平行四边形,边CD与⊙O交于点E,连接AE.
(1)求证:AE=AD;
(2)若∠B=72°,求证:点E是的中点.
参考答案
一.选择题(共10小题,满分50分)
1.解:A、经过不共线的三点可以作一个圆,所以A选项的说法错误;
B、三角形的外心到三个顶点的距离相等,所以B选项的说法错误;
C、在同圆或等圆中,相等的圆心角所对的弧相等,所以选项C说法错误;
D、等弧所对的圆心角相等,所以D选项的说法正确;
故选:D.
2.解:∵点P在圆O的外部,
∴点P到圆心O的距离大于8,
故选:A.
3.解:A、过一点A的圆的圆心可以是平面上任意点(A点外),故本选项错误,
B、在同一平面内,过两点A、B的圆的圆心在线段AB的垂直平分线上,故正确,
C、错误,A、B、C三点共线时,不符合题意.
D、过四点A、B、C、D的圆可以存在,故本选项错误,
故选:B.
4.解:过不在同一直线上的三点有且只有一个圆,所以①错误;
平分弦(非直径)的直径垂直于弦,所以②错误;
三角形的外心到三角形三个顶点的距离相等,所以③正确;
同弧或等弧所对的圆周角相等,所以④正确;
圆内接平行四边形的对角相等且互补,此时四边形是矩形,所以⑤正确.
故选:D.
5.解:∵∠AOC和∠ABC是同弧所对的圆心角和圆周角,
∴∠AOC=2∠ABC=120°;
故选:B.
6.解:∵三角形的外心是三角形三边垂直平分线的交点,
∴A、B、C选项错误,D选项正确,
故选:D.
7.解:连接BG,
在△BEF中,BE=2,∠BFE=30°,
∴EF=2BE=4,BF=BE=2,
∵G是EF的中点,
∴BG=EF=2,
∴G在⊙B上,且半径为2,
∴当G在DB的延长线上时,DG最大,
∵BE=2,BF=2,点E是AB的中点,点F是BC的中点,
∴AB=4,BC=4,
∴BD==8,
∴DG的最大值为8+2=10,
故选:C.
8.解:如图,设AO与BC交于点D,
∵∠AOB=60°,
∴∠C=∠AOB=30°,
∵AB=AC,
∴=,
∴AD⊥BC,
∴BD=CD,
在Rt△ACD中,CD=AC cos30°=2×=,
∴BC=2CD=2,
故选:D.
9.解:①半径不是弦,本小题说法是假命题;
②任意三角形都有且只有一个外接圆,本小题说法是真命题;
③平分弦(不是直径)的直径垂直于这条弦,本小题说法是假命题;
④半圆所对的圆周角是90°,本小题说法是真命题;
⑤在同圆或等圆中,相等的圆周角所对的弧相等,本小题说法是假命题;
故选:A.
10.解:∵△ABC是等边三角形,
∴∠ABC=∠BAC=60°,AC=AB=3,
∵∠PAB=∠ACP,
∴∠PAC+∠ACP=60°,
∴∠APC=120°,
∴点P的运动轨迹是,
设所在圆的圆心为O,当O、P、B共线时,PB长度最小,设OB交AC于D,如图所示:
此时PA=PC,OB⊥AC,
则AD=CD=AC=,∠PAC=∠ACP=30°,∠ABD=∠ABC=30°,
∴PD=,BD=,
∴PB=BD﹣PD=﹣=.
故选:B.
二.填空题(共6小题,满分30分)
11.解:x2﹣7x+12=0,
(x﹣3)(x﹣4)=0,
解得:x1=3,x2=4,
①当直角边分别为3,4时,
斜边为:=5,
此时直角三角形外接圆的直径为5,
②当直角边为3,斜边为4时,
此时直角三角形外接圆直径为4.
故答案为4或5.
12.解:∵直角边长分别为6和8,
∴斜边是10,
∴这个直角三角形的外接圆的半径为5,
故答案为:5.
13.解:如图,取AC的中点N,连接MN,BN.
∵∠ABC=90°,AB=8,BC=6,
∴AC=10,
∵AN=NC,
∴BN=AC=5,
∵AN=NC,DM=MC,
∴MN==2,
∴BM≤BN+NM,
∴BM≤5+2=7,
即BM的最大值是7.
故答案为7.
14.解:∵∠BOC=2∠A=2×45°=90°,
而OB=OC,
∴△OBC为等腰直角三角形,
∴∠OCB=45°,
∴cos∠OCB=.
故答案为.
15.解:在x轴上取一点E(﹣12,0),连接PE.
∵B(﹣6,0),A(﹣6,8),
∴OB=BE=6,AE==10,
∵OM=PM,OB=BE,
∴BM=PE,
∵点P在⊙A上运动,
∴P,A,B共线时,可以取得最大值或最小值,最大值=EP′=10+4=14,最小值EP″=10﹣4=6,
∴m=7,n=3,
∴m﹣n=4,
故答案为:4.
16.解:取AB的中点T,连接FT,DT.
∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AD=4,AT=TB=1,
∴DT===,
∵BF⊥AE,
∴∠AFB=90°,
∵AT=TB,
∴FT=AB=1,
∴DF≥DT﹣FT=﹣1,
∴DF的最小值为﹣1.
故答案为:﹣1.
三.解答题(共4小题,满分40分)
17.解:∵∠C=90°,AC=6,BC=8,
∴AB==10,
∴Rt△ABC的外接圆的半径为5,
面积为π×52=25π.
18.解:(1)如图1,连接CO,AO,
∵CA=CB,OA=OB,OC=OC,
∴△COA≌△COB(SSS),
∴∠ACO=∠BCO,
∵OC=OB,
∴∠BCO=∠CBD,
∴∠C=2∠CBD;
(2)如图2,作⊙O的直径AK,连接BK,
则∠ABK=90°,∠C=∠K,
∵AB=6,sinC=,
∴sinK==,
∴AK=10,
∴⊙O的半径为5.
19.解:MB+MC=MA.
理由如下:截取ME=MC,
∵∠AMC=∠ABC=60°,
∴△MEC为等边三角形,
∴CE=CM,∠MCE=60°,
而∠ACB=60°,
∴∠ACE=∠BCM,
在△CAE和△CBM中,
,
∴△CAE≌△CBM,
∴AE=MB,
∴MB+MC=MA.
20.证明:(1)∵四边形ABCD是平行四边形,
∴∠ABC=∠D,
∵四边形ABCE为⊙O的内接四边形,
∴∠ABC+∠AEC=180°,
∵∠AED+∠AEC=180°,
∴∠ABC=∠AED,
∴∠D=∠AED,
∴AE=AD;
(2)∵AB=AC,∠B=72°,
∴∠ABC=∠ACB=72°,∠AEC=180°﹣∠B=108°,
∴∠BAC=180°﹣72°×2=36°,
∵AB∥CD,
∴∠ACE=∠BAC=36°,
∴∠EAC=180°﹣∠AEC﹣∠ACE=36°,
∴∠ACE=∠EAC,
∴=,即点E是的中点.
