2021-2022学年北师大版九年级数学下册3.2圆的对称性 同步达标测试题 (Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.2圆的对称性 同步达标测试题 (Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 148.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 20:09:40 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《3-2圆的对称性》同步达标测试题(附答案)
一.选择题(共10小题,满分50分)
1.下列说法正确的是( )
A.等弧所对的弦相等 B.平分弦的直径垂直弦并平分弦所对的弧
C.相等的弦所对的圆心角相等 D.相等的圆心角所对的弧相等
2.下列命题是真命题的是( )
A.相等的弦所对的弧相等
B.圆心角相等,其所对的弦相等
C.在同圆或等圆中,圆心角不等,所对的弦不相等
D.弦相等,它所对的圆心角相等
3.如图,AB,CD是⊙O的直径,=,若∠AOE=32°,则∠COE的度数是( )
A.32° B.60° C.68° D.64°
4.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,则⊙O的周长为( )
A.5πcm B.6πcm C.9πcm D.8πcm
5.如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
A.AB=AD B.BC=CD C. D.∠BCA=∠DCA
6.如图,AB是圆O的直径,BC、CD、DA是圆O的弦,且BC=CD=DA,则∠BCD等于( )
A.100° B.110° C.120° D.135°
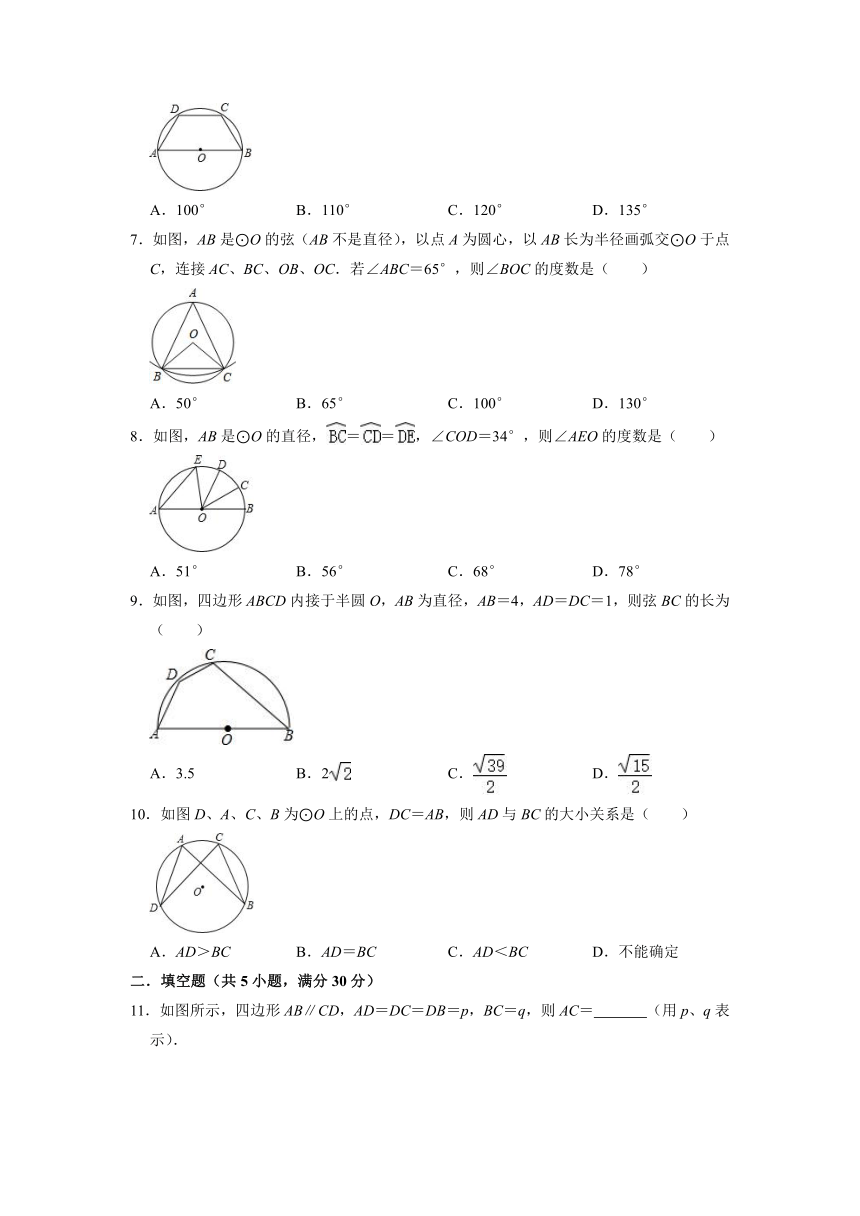
7.如图,AB是⊙O的弦(AB不是直径),以点A为圆心,以AB长为半径画弧交⊙O于点C,连接AC、BC、OB、OC.若∠ABC=65°,则∠BOC的度数是( )
A.50° B.65° C.100° D.130°
8.如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是( )
A.51° B.56° C.68° D.78°
9.如图,四边形ABCD内接于半圆O,AB为直径,AB=4,AD=DC=1,则弦BC的长为( )
A.3.5 B.2 C. D.
10.如图D、A、C、B为⊙O上的点,DC=AB,则AD与BC的大小关系是( )
A.AD>BC B.AD=BC C.AD<BC D.不能确定
二.填空题(共5小题,满分30分)
11.如图所示,四边形AB∥CD,AD=DC=DB=p,BC=q,则AC= (用p、q表示).
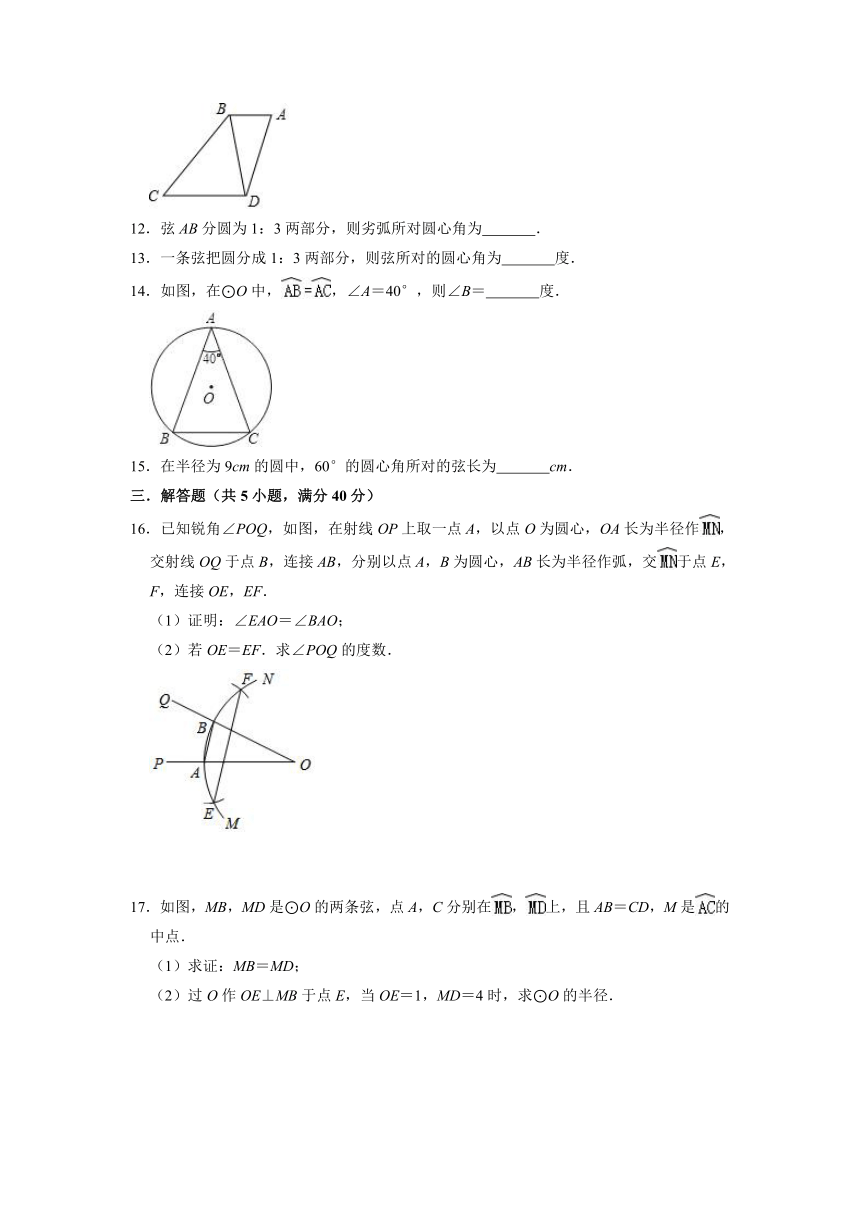
12.弦AB分圆为1:3两部分,则劣弧所对圆心角为 .
13.一条弦把圆分成1:3两部分,则弦所对的圆心角为 度.
14.如图,在⊙O中,,∠A=40°,则∠B= 度.
15.在半径为9cm的圆中,60°的圆心角所对的弦长为 cm.
三.解答题(共5小题,满分40分)
16.已知锐角∠POQ,如图,在射线OP上取一点A,以点O为圆心,OA长为半径作,交射线OQ于点B,连接AB,分别以点A,B为圆心,AB长为半径作弧,交于点E,F,连接OE,EF.
(1)证明:∠EAO=∠BAO;
(2)若OE=EF.求∠POQ的度数.
17.如图,MB,MD是⊙O的两条弦,点A,C分别在,上,且AB=CD,M是的中点.
(1)求证:MB=MD;
(2)过O作OE⊥MB于点E,当OE=1,MD=4时,求⊙O的半径.
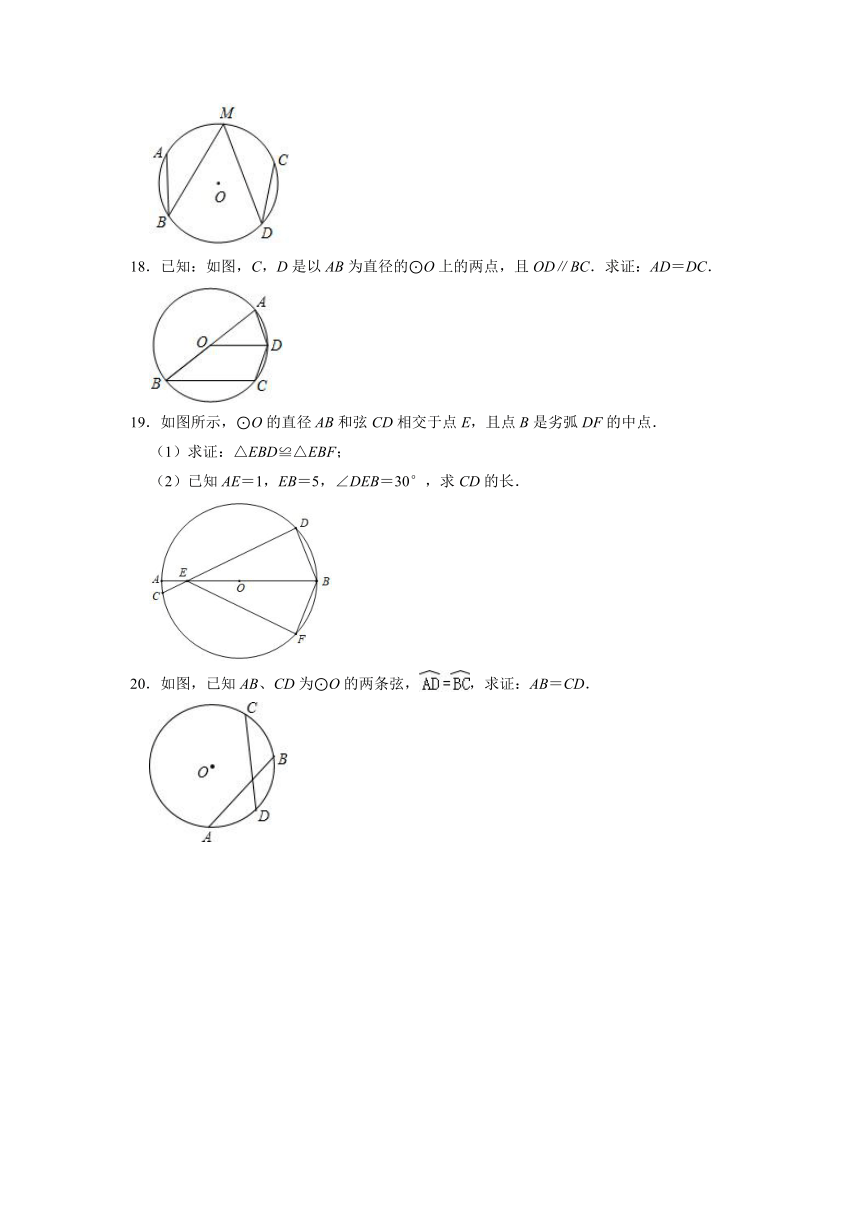
18.已知:如图,C,D是以AB为直径的⊙O上的两点,且OD∥BC.求证:AD=DC.
19.如图所示,⊙O的直径AB和弦CD相交于点E,且点B是劣弧DF的中点.
(1)求证:△EBD≌△EBF;
(2)已知AE=1,EB=5,∠DEB=30°,求CD的长.
20.如图,已知AB、CD为⊙O的两条弦,,求证:AB=CD.
参考答案
一.选择题(共10小题,满分50分)
1.解:A、正确.本选项符合题意.
B、错误.应该是平分弦(此弦非直径)的直径垂直弦并平分弦所对的弧,本选项不符合题意.
C、错误,必须在同圆或等圆中,本选项不符合题意.
D、错误.必须在同圆或等圆中,本选项不符合题意.
故选:A.
2.解:A、B、D结论若成立,都必须以“在同圆或等圆中”为前提条件,所以A、B、D错误;
故选:C.
3.解:∵=,
∴∠BOD=∠AOE=32°,
∵∠BOD=∠AOC,
∴∠AOC=32°
∴∠COE=32°+32°=64°.故选:D.
4.解:如图,连接OD、OC.
∵AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,
∴==,
∴∠AOD=∠DOC=∠BOC=60°.
又OA=OD,
∴△AOD是等边三角形,
∴OA=AD=4cm,
∴⊙O的周长=2×4π=8π(cm).故选:D.
5.解:A、∵∠ACB与∠ACD的大小关系不确定,∴AB与AD不一定相等,故本选项错误;
B、∵AC平分∠BAD,∴∠BAC=∠DAC,∴=,∴BC=CD,故本选项正确;
C、∵∠ACB与∠ACD的大小关系不确定,∴与不一定相等,故本选项错误;
D、∠BCA与∠DCA的大小关系不确定,故本选项错误.
故选:B.
6.解:连接OC、OD,
∵BC=CD=DA,
∴∠COB=∠COD=∠DOA,
∵∠COB+∠COD+∠DOA=180°,
∴∠COB=∠COD=∠DOA=60°,
∴∠BCD=×2(180°﹣60°)=120°.
故选:C.
7.解:由题意可得:AB=AC,
∵∠ABC=65°,
∴∠ACB=65°,
∴∠A=50°,
∴∠BOC=100°,
故选:C.
8.解:如图,∵==,∠COD=34°,
∴∠BOC=∠EOD=∠COD=34°,
∴∠AOE=180°﹣∠EOD﹣∠COD﹣∠BOC=78°.
又∵OA=OE,
∴∠AEO=∠OAE,
∴∠AEO=×(180°﹣78°)=51°.
故选:A.
9.解:如图,连AC、BD,过D作DE⊥AC于E.
∴∠ADB=∠ACB=90°,∠ABD=∠CAD.
∵BD==.
∵AD=DC=1,
∴∠DAC=∠DCA,
∵∠DCA=∠ABD,
cos∠CAD=cos∠ABD==.
∴AE=AD cos∠CAD=,
∴AC=2AE=,
∴BC==.
故选:A.
10.解:∵DC=AB,
∴=,
∴=,
∴AD=BD.
故选:B.
二.填空题(共5小题,满分30分)
11.解:延长CD交半径为p的⊙D于E点,连接AE.显然A、B、C在⊙D上.
∵AB∥CD
∴=,
∴BC=AE=q.
在△ACE中,∠CAE=90°,CE=2p,AE=q,
故AC==.
故答案为:.
12.解:设弦AB分圆的两部分别为x,3x,
∴x+3x=360°,
解得:x=90,
则劣弧所对圆心角为90°.
故答案为:90°
13.解:∵一条弦把圆分成1:3两部分,
∴整个圆分为四等分,
则劣弧的度数为360°÷4=90°,
∴弦所对的圆心角为90°.
14.解:∵,
∴AB=AC,
∵∠A=40°,
∴∠B=∠C=(180°﹣∠A)÷2=70°.
15.解:由题意知,设圆心为O,60°的圆心角的两边与圆的交点分别为A,B,则△AOB是等边三角形,∴AO=AB=OB=9cm.
三.解答题(共5小题,满分40分)
16.(1)证明:连接AE、OE、OF,如图所示,
由题意得:OB=OE=OA,AE=AB,
∴∠EAO=∠AEO,∠BAO=∠ABO,,
∴∠AOE=∠AOB,
∴∠EAO=∠BAO;
(2)解:∵OE=OF,OE=EF,
∴OE=OF=EF,
∴∠EOF=60°,
∵AE=BF=AB,
∴,
∴∠AOE=∠BOF=∠AOB,
∴∠POQ=∠EOF=20°.
17.(1)证明:∵AB=CD,
∴=,
∵M是的中点,
∴=,
∴=,
∴BM=DM.
(2)解:如图,连接OM.
∵DM=BM=4,OE⊥BM,
∴EM=BE=2,
∵OE=1,∠OEM=90°,
∴OM===,
∴⊙O的半径为.
18.证明:连接OC,如图,
∵OD∥BC,
∴∠1=∠B,∠2=∠3,
又∵OB=OC,
∴∠B=∠3,
∴∠1=∠2,
∴AD=DC.
19.解:(1)连接OD、OF,
∵B是劣弧DF的中点.
∴,
∴,
∴BD=BF,∠DBE=∠EBF,
在△EBD和△EBF中,
∵,
∴△EBD≌△EBF(SAS);
(2)∵AE=1,EB=5,
∴AB=6,
∵AB是⊙O的直径,
∴OD=OA=3,OE=3﹣1=2,
过O作OG⊥CD于G,则CD=2DG,
∵∠DEB=30°,∠EGO=90°,
∴OG=OE=1,
由勾股定理得:DG===2,
∴CD=2DG=4.
20.解:∵,
∴,
即:,
∴AB=CD.
一.选择题(共10小题,满分50分)
1.下列说法正确的是( )
A.等弧所对的弦相等 B.平分弦的直径垂直弦并平分弦所对的弧
C.相等的弦所对的圆心角相等 D.相等的圆心角所对的弧相等
2.下列命题是真命题的是( )
A.相等的弦所对的弧相等
B.圆心角相等,其所对的弦相等
C.在同圆或等圆中,圆心角不等,所对的弦不相等
D.弦相等,它所对的圆心角相等
3.如图,AB,CD是⊙O的直径,=,若∠AOE=32°,则∠COE的度数是( )
A.32° B.60° C.68° D.64°
4.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,则⊙O的周长为( )
A.5πcm B.6πcm C.9πcm D.8πcm
5.如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
A.AB=AD B.BC=CD C. D.∠BCA=∠DCA
6.如图,AB是圆O的直径,BC、CD、DA是圆O的弦,且BC=CD=DA,则∠BCD等于( )
A.100° B.110° C.120° D.135°
7.如图,AB是⊙O的弦(AB不是直径),以点A为圆心,以AB长为半径画弧交⊙O于点C,连接AC、BC、OB、OC.若∠ABC=65°,则∠BOC的度数是( )
A.50° B.65° C.100° D.130°
8.如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是( )
A.51° B.56° C.68° D.78°
9.如图,四边形ABCD内接于半圆O,AB为直径,AB=4,AD=DC=1,则弦BC的长为( )
A.3.5 B.2 C. D.
10.如图D、A、C、B为⊙O上的点,DC=AB,则AD与BC的大小关系是( )
A.AD>BC B.AD=BC C.AD<BC D.不能确定
二.填空题(共5小题,满分30分)
11.如图所示,四边形AB∥CD,AD=DC=DB=p,BC=q,则AC= (用p、q表示).
12.弦AB分圆为1:3两部分,则劣弧所对圆心角为 .
13.一条弦把圆分成1:3两部分,则弦所对的圆心角为 度.
14.如图,在⊙O中,,∠A=40°,则∠B= 度.
15.在半径为9cm的圆中,60°的圆心角所对的弦长为 cm.
三.解答题(共5小题,满分40分)
16.已知锐角∠POQ,如图,在射线OP上取一点A,以点O为圆心,OA长为半径作,交射线OQ于点B,连接AB,分别以点A,B为圆心,AB长为半径作弧,交于点E,F,连接OE,EF.
(1)证明:∠EAO=∠BAO;
(2)若OE=EF.求∠POQ的度数.
17.如图,MB,MD是⊙O的两条弦,点A,C分别在,上,且AB=CD,M是的中点.
(1)求证:MB=MD;
(2)过O作OE⊥MB于点E,当OE=1,MD=4时,求⊙O的半径.
18.已知:如图,C,D是以AB为直径的⊙O上的两点,且OD∥BC.求证:AD=DC.
19.如图所示,⊙O的直径AB和弦CD相交于点E,且点B是劣弧DF的中点.
(1)求证:△EBD≌△EBF;
(2)已知AE=1,EB=5,∠DEB=30°,求CD的长.
20.如图,已知AB、CD为⊙O的两条弦,,求证:AB=CD.
参考答案
一.选择题(共10小题,满分50分)
1.解:A、正确.本选项符合题意.
B、错误.应该是平分弦(此弦非直径)的直径垂直弦并平分弦所对的弧,本选项不符合题意.
C、错误,必须在同圆或等圆中,本选项不符合题意.
D、错误.必须在同圆或等圆中,本选项不符合题意.
故选:A.
2.解:A、B、D结论若成立,都必须以“在同圆或等圆中”为前提条件,所以A、B、D错误;
故选:C.
3.解:∵=,
∴∠BOD=∠AOE=32°,
∵∠BOD=∠AOC,
∴∠AOC=32°
∴∠COE=32°+32°=64°.故选:D.
4.解:如图,连接OD、OC.
∵AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,
∴==,
∴∠AOD=∠DOC=∠BOC=60°.
又OA=OD,
∴△AOD是等边三角形,
∴OA=AD=4cm,
∴⊙O的周长=2×4π=8π(cm).故选:D.
5.解:A、∵∠ACB与∠ACD的大小关系不确定,∴AB与AD不一定相等,故本选项错误;
B、∵AC平分∠BAD,∴∠BAC=∠DAC,∴=,∴BC=CD,故本选项正确;
C、∵∠ACB与∠ACD的大小关系不确定,∴与不一定相等,故本选项错误;
D、∠BCA与∠DCA的大小关系不确定,故本选项错误.
故选:B.
6.解:连接OC、OD,
∵BC=CD=DA,
∴∠COB=∠COD=∠DOA,
∵∠COB+∠COD+∠DOA=180°,
∴∠COB=∠COD=∠DOA=60°,
∴∠BCD=×2(180°﹣60°)=120°.
故选:C.
7.解:由题意可得:AB=AC,
∵∠ABC=65°,
∴∠ACB=65°,
∴∠A=50°,
∴∠BOC=100°,
故选:C.
8.解:如图,∵==,∠COD=34°,
∴∠BOC=∠EOD=∠COD=34°,
∴∠AOE=180°﹣∠EOD﹣∠COD﹣∠BOC=78°.
又∵OA=OE,
∴∠AEO=∠OAE,
∴∠AEO=×(180°﹣78°)=51°.
故选:A.
9.解:如图,连AC、BD,过D作DE⊥AC于E.
∴∠ADB=∠ACB=90°,∠ABD=∠CAD.
∵BD==.
∵AD=DC=1,
∴∠DAC=∠DCA,
∵∠DCA=∠ABD,
cos∠CAD=cos∠ABD==.
∴AE=AD cos∠CAD=,
∴AC=2AE=,
∴BC==.
故选:A.
10.解:∵DC=AB,
∴=,
∴=,
∴AD=BD.
故选:B.
二.填空题(共5小题,满分30分)
11.解:延长CD交半径为p的⊙D于E点,连接AE.显然A、B、C在⊙D上.
∵AB∥CD
∴=,
∴BC=AE=q.
在△ACE中,∠CAE=90°,CE=2p,AE=q,
故AC==.
故答案为:.
12.解:设弦AB分圆的两部分别为x,3x,
∴x+3x=360°,
解得:x=90,
则劣弧所对圆心角为90°.
故答案为:90°
13.解:∵一条弦把圆分成1:3两部分,
∴整个圆分为四等分,
则劣弧的度数为360°÷4=90°,
∴弦所对的圆心角为90°.
14.解:∵,
∴AB=AC,
∵∠A=40°,
∴∠B=∠C=(180°﹣∠A)÷2=70°.
15.解:由题意知,设圆心为O,60°的圆心角的两边与圆的交点分别为A,B,则△AOB是等边三角形,∴AO=AB=OB=9cm.
三.解答题(共5小题,满分40分)
16.(1)证明:连接AE、OE、OF,如图所示,
由题意得:OB=OE=OA,AE=AB,
∴∠EAO=∠AEO,∠BAO=∠ABO,,
∴∠AOE=∠AOB,
∴∠EAO=∠BAO;
(2)解:∵OE=OF,OE=EF,
∴OE=OF=EF,
∴∠EOF=60°,
∵AE=BF=AB,
∴,
∴∠AOE=∠BOF=∠AOB,
∴∠POQ=∠EOF=20°.
17.(1)证明:∵AB=CD,
∴=,
∵M是的中点,
∴=,
∴=,
∴BM=DM.
(2)解:如图,连接OM.
∵DM=BM=4,OE⊥BM,
∴EM=BE=2,
∵OE=1,∠OEM=90°,
∴OM===,
∴⊙O的半径为.
18.证明:连接OC,如图,
∵OD∥BC,
∴∠1=∠B,∠2=∠3,
又∵OB=OC,
∴∠B=∠3,
∴∠1=∠2,
∴AD=DC.
19.解:(1)连接OD、OF,
∵B是劣弧DF的中点.
∴,
∴,
∴BD=BF,∠DBE=∠EBF,
在△EBD和△EBF中,
∵,
∴△EBD≌△EBF(SAS);
(2)∵AE=1,EB=5,
∴AB=6,
∵AB是⊙O的直径,
∴OD=OA=3,OE=3﹣1=2,
过O作OG⊥CD于G,则CD=2DG,
∵∠DEB=30°,∠EGO=90°,
∴OG=OE=1,
由勾股定理得:DG===2,
∴CD=2DG=4.
20.解:∵,
∴,
即:,
∴AB=CD.
