2021_2022学年数学五年级下册 探索图形同步练习(含答案)人教版
文档属性
| 名称 | 2021_2022学年数学五年级下册 探索图形同步练习(含答案)人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 167.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 06:50:12 | ||
图片预览




文档简介
探索图形
一、选择题(共13题)
1.用8个相同的小正方体拼成一个大正方体,拿走一个小正方体后表面积( )原来拼成的大正方体的表面积。
A.小于 B.等于 C.大于
2.将一个表面涂色的大正方体切成27个小正方体,三面涂色的小正方体有( )个.
A.8 B.15 C.27
3.下图由( )个小立方体组成的。
A.12 B.13 C.14 D.15
4.一个表面涂色的长方体木块,长、宽、高都是整数厘米,把它切割成若干棱长为的小正方体木块。如果存在恰有五个面涂色的小正方体,那么这样的小正方体最多有( )个。(请选择)
A.许多 B.8 C.4 D.2
5.如下图,把一个棱长的正方体木块六个面都涂上红色,然后锯成棱长都是的小正方体木块,可以得到涂色面数不同的小正方体木块,那么得到的小正方体块数最多的一类是( )。
A.0面涂色 B.一面涂色 C.两面涂色 D.三面涂色
6.棱长是2dm的正方体能切成( )个棱长为1dm的正方体。
A.2 B.4 C.8 D.16
7.用棱长1cm的小正方体拼成如上的大正方体后,把它们的表面积涂上颜色。三面、两面、一面涂色的分别为( )个。
A.6、8、12 B.8、12、6 C.12、6、8 D.8、6、12
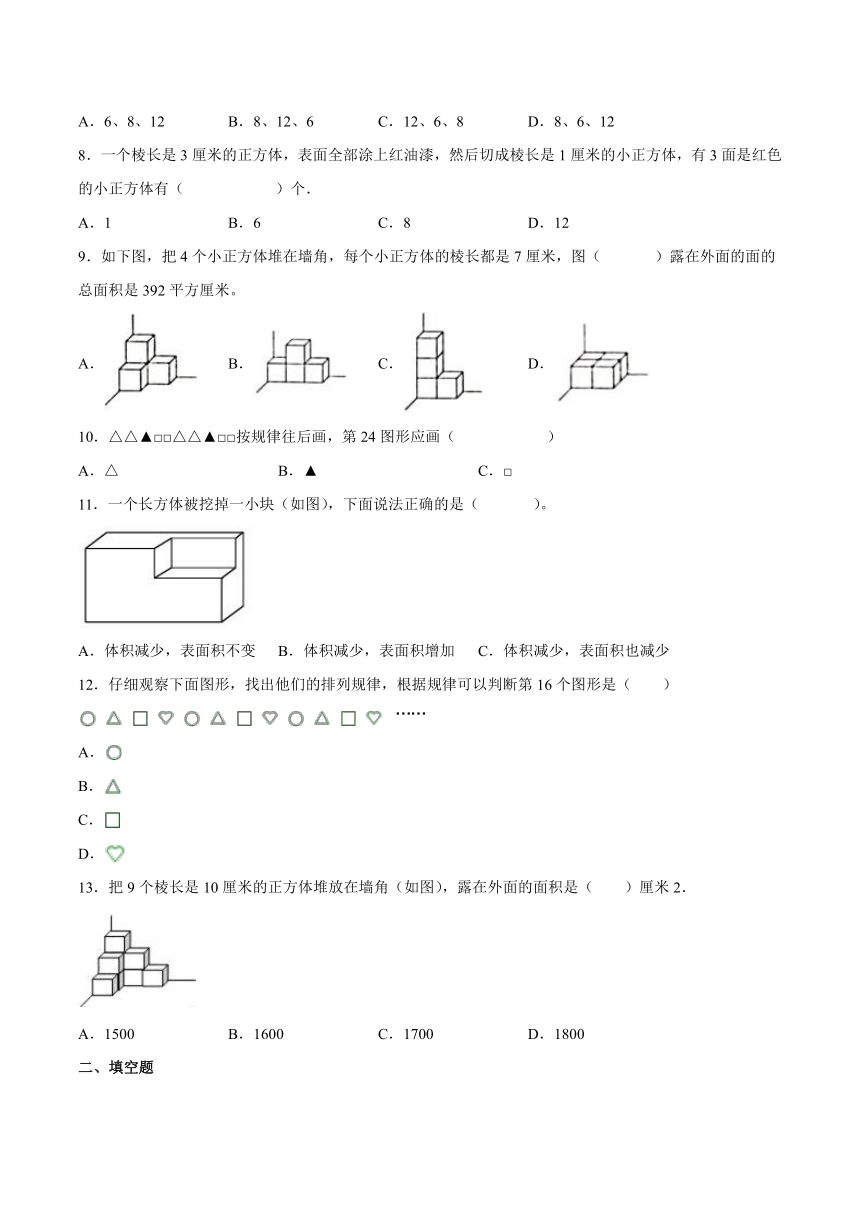
一个棱长是3厘米的正方体,表面全部涂上红油漆,然后切成棱长是1厘米的小正方体,有3面是红色的小正方体有( )个.
A.1 B.6 C.8 D.12
9.如下图,把4个小正方体堆在墙角,每个小正方体的棱长都是7厘米,图( )露在外面的面的总面积是392平方厘米。
A. B. C. D.
10.△△▲□□△△▲□□按规律往后画,第24图形应画( )
A.△ B.▲ C.□
11.一个长方体被挖掉一小块(如图),下面说法正确的是( )。
A.体积减少,表面积不变 B.体积减少,表面积增加 C.体积减少,表面积也减少
12.仔细观察下面图形,找出他们的排列规律,根据规律可以判断第16个图形是( )
A.
B.
C.
D.
13.把9个棱长是10厘米的正方体堆放在墙角(如图),露在外面的面积是( )厘米2.
A.1500 B.1600 C.1700 D.1800
二、填空题
14.用棱长1cm的小正方体拼成棱长是4cm的大正方体,然后把大正方体的表面涂上颜色。那么小正方体中,三面涂色的有( )个,没有涂色的有( )个。
15.图中每个正方体的棱长都是3厘米.下面各图的表面积分别是多少?
平方厘米; 平方厘米; 平方厘米; 个面积是1854平方厘米.
16.如图是由若干个棱长都是1厘米的小正方体拼成的
(1)左图中共有 个小正方体,至少加上 个这样的小正方体就变成一个长方体.
(2)如图的表面积是 平方厘米.
(3)从右边看这图形的形状是 .
17.淘气用11个大小相同的正方体搭成如左下图所示的几何体,然后把所有表面(含底面)涂成了红色,那么恰好有四个面涂色的正方体有( )个。
三、解答题
18.将一个长4cm,宽3cm,高2cm的长方体的六个面涂上红色,然后把这个长方体切割成棱长为1cm的小正方体。这些小正方体中恰好有两个面涂上红色的有多少个?
19.如图,是一个长为5厘米,宽为4厘米、高为3厘米的长方体,在它的表面涂上颜色后再截成棱长为1厘米的小正方体,其中三面、两面和一面被涂色的小正方体有多少个?
20.一个大正方体,先在它的每个面上都涂上红色,再把它切成棱长是的小正方体。已知两面涂色的小正方体有96个,原来大正方体的体积是多少立方厘米?
21.一个长方体木块(如图),长是,宽是,高是,先在它的六个面上都涂上色,然后把它锯成棱长都是
的小正方体木块。在锯成的小正方体木块中,三面涂色的有多少块?两面、一面涂色的各有多少块?六个面都没有涂色的有多少块?
参考答案:
1.B
【详解】
拿走一个小正方体后表面积等于原来拼成的大正方体的表面积;
故答案为:B。
2.A
【详解】
仔细观察由27个小正方体组成的大正方体,三面涂色的小正方体在顶点处,因为有8个顶点,所以有8个这样的小正方体。
故答案为A。
3.B
【详解】
该立体图形由7+5+1=13(个)个小立方体组成的
故答案为:B
4.D
【详解】
由分析可知只有长方体两端的两个小正方体是5个面涂色,如下图:(图形不唯一)
故答案为:D。
5.C
【详解】
根据分析,中间只有1个小正方体,正方体有6个面,一面涂色的有6个;有12条棱,两面涂色的有12个;有8个顶点,三面涂色的有8个。
故答案为:C
6.C
【详解】
2÷1=2(个)
2×2×2=8(个)
故答案为:C。
7.B
【详解】
根据分析可得:
一面涂色:(3-2)×(3-2)×6
=1×1×6
=6(个)
两面涂色:(3-2)×12
=1×12
=12(个)
三面涂色:8个
故答案为:B。
8.C
【详解】
因为3面图色的在8个顶点上,所以一共有8个。
故答案为:C
9.D
【详解】
A.(3+3+3)×(7×7)
=9×49
=441(平方厘米);
B.(4+2+3)×(7×7)
=9×49
=441(平方厘米);
C.(4+3+2)×(7×7)
=9×49
=441(平方厘米);
D.(2+2+4)×(7×7)
=8×49
=392(平方厘米)
故答案为:D。
10.C
【详解】
24÷5=4(组) 4(个),说明第24个图形应该是第5组中的第4个,即是□。
故答案为:C
11.A
【详解】
如图中一个长方体被挖掉一小块,体积减少,表面积不变。
故答案为:A
12.D
【详解】
由图可知图形时按圆形、三角形、正方形、心形循环排列的,每四个图形一循环,因为16÷4=4,所以16个图形为心形.
13.C
【详解】
(10×10)×(6+5+6),
=100×17
=1700(厘米2)
答:露在外面的面积是1700厘米2.
故选C
14. 8 8
【详解】
由分析可知:三面涂色的有8个;没有涂色的有(4-2)×(4-2)×(4-2)=8个。
15.54;90;126;51
【详解】
试题分析:每个正方体的棱长都是3厘米,则每个小正方形面的面积都是32平方厘米;所以1个正方体的表面积是6×32平方厘米,可以写成(2+4)×32平方厘米,
2个正方体拼组后减少了两个面,所以表面积是10×32平方厘米;可以写成(2+2×4)×32平方厘米,
3个正方体拼组在一起减少了4个面,表面积是14×32平方厘米,可以写成(2+3×4)×32平方厘米,
所以每增加一个小正方体就增加了4个面…
由此若是n个正方体拼组一起表面积就可以写成(2+n×4)×32平方厘米,由此即可解决问题.
解:1个正方体的表面积是(2+4)×32=54平方厘米;
2个正方体的表面积是(2+2×4)×32=90平方厘米;
3个正方体的表面积是(2+3×4)×32=126平方厘米;
(2+n×4)×32=1854,
(2+n×4)×9=1854,
2+n×4=206,
n×4=204,
n=51.
答:1个正方体的表面积是54平方厘米;2个正方体的表面积是90平方厘米;3个正方体的表面积是126平方厘米;51个面积是1854平方厘米.
故答案为54;90;126;51.
16.(1)14;13;(2)46;(3).
【详解】
试题分析:(1)观察图形可知:最下面一行中有3×3=9个小正方体,中间一行中有4个小正方体,上面一行只有1个小正方体;可以组成的正方体的棱长最少是3个小正方体的棱长,由此可以求得需要的小正方体的总个数解决问题;
(2)上下面看到的正方体的面有3×3=9个面;前后、左右看到的小正方体的面都是3+3+1=7个面;
(3)从右边看到的图形是:下面3个正方形,中间3个正方形,上面1个正方形.
解:(1)图形中小正方体的个数为:9+4+1=14(个),
组成一个大正方体至少还需要小正方体的个数为:3×3×3﹣14=27﹣14=13(个),
(2)1×1×(9×2+7×4),
=1×46,
=46(平方厘米),
答:这个图形的表面积是46平方厘米;
(3)从右边看这图形的形状是:
故答案为(1)14;13;(2)46;(3).
17.6
【详解】
由分析可知:有四个面涂色的正方体上层有2个,下层有4个,共6个。
18.12个
【详解】
2×4+1×4=12(个)
19.8个;24个;22个
【详解】
长方体有8个顶点,所以三面被涂色的小正方体有8个。
长方体有12条棱,其中每条长上有3个小正方体,宽上有2个小正方体,高上有1个小正方体,所以两面被涂色的小正方体有:(3+2+1)×4=24(个)。
长方体有6个面,前面和后面,每个面上中间部分的小正方体有3个;左面和右面,每个面上中间部分的小正方体有2个;上面和下面,每个面上中间部分的小正方体有6个,所以一面被涂色的小正方体有:(3+2+6)×2=22(个)。
答:三面被涂色的小正方体有8个,两面被涂色的小正方体有24个,一面被涂色的小正方体有22个。
20.
【详解】
(个)
答:原来大正方体的体积是。
21.在锯成的小正方体木块中,三面涂色的有8块,两面涂色的有24块,一面涂色的有22块,六个面都没有涂色的有6块。
【详解】
由分析得:
三面涂色的有:1×8=8(块)
两面涂色的有:
(块)
一面涂色的有:
(块)
(块)
一、选择题(共13题)
1.用8个相同的小正方体拼成一个大正方体,拿走一个小正方体后表面积( )原来拼成的大正方体的表面积。
A.小于 B.等于 C.大于
2.将一个表面涂色的大正方体切成27个小正方体,三面涂色的小正方体有( )个.
A.8 B.15 C.27
3.下图由( )个小立方体组成的。
A.12 B.13 C.14 D.15
4.一个表面涂色的长方体木块,长、宽、高都是整数厘米,把它切割成若干棱长为的小正方体木块。如果存在恰有五个面涂色的小正方体,那么这样的小正方体最多有( )个。(请选择)
A.许多 B.8 C.4 D.2
5.如下图,把一个棱长的正方体木块六个面都涂上红色,然后锯成棱长都是的小正方体木块,可以得到涂色面数不同的小正方体木块,那么得到的小正方体块数最多的一类是( )。
A.0面涂色 B.一面涂色 C.两面涂色 D.三面涂色
6.棱长是2dm的正方体能切成( )个棱长为1dm的正方体。
A.2 B.4 C.8 D.16
7.用棱长1cm的小正方体拼成如上的大正方体后,把它们的表面积涂上颜色。三面、两面、一面涂色的分别为( )个。
A.6、8、12 B.8、12、6 C.12、6、8 D.8、6、12
一个棱长是3厘米的正方体,表面全部涂上红油漆,然后切成棱长是1厘米的小正方体,有3面是红色的小正方体有( )个.
A.1 B.6 C.8 D.12
9.如下图,把4个小正方体堆在墙角,每个小正方体的棱长都是7厘米,图( )露在外面的面的总面积是392平方厘米。
A. B. C. D.
10.△△▲□□△△▲□□按规律往后画,第24图形应画( )
A.△ B.▲ C.□
11.一个长方体被挖掉一小块(如图),下面说法正确的是( )。
A.体积减少,表面积不变 B.体积减少,表面积增加 C.体积减少,表面积也减少
12.仔细观察下面图形,找出他们的排列规律,根据规律可以判断第16个图形是( )
A.
B.
C.
D.
13.把9个棱长是10厘米的正方体堆放在墙角(如图),露在外面的面积是( )厘米2.
A.1500 B.1600 C.1700 D.1800
二、填空题
14.用棱长1cm的小正方体拼成棱长是4cm的大正方体,然后把大正方体的表面涂上颜色。那么小正方体中,三面涂色的有( )个,没有涂色的有( )个。
15.图中每个正方体的棱长都是3厘米.下面各图的表面积分别是多少?
平方厘米; 平方厘米; 平方厘米; 个面积是1854平方厘米.
16.如图是由若干个棱长都是1厘米的小正方体拼成的
(1)左图中共有 个小正方体,至少加上 个这样的小正方体就变成一个长方体.
(2)如图的表面积是 平方厘米.
(3)从右边看这图形的形状是 .
17.淘气用11个大小相同的正方体搭成如左下图所示的几何体,然后把所有表面(含底面)涂成了红色,那么恰好有四个面涂色的正方体有( )个。
三、解答题
18.将一个长4cm,宽3cm,高2cm的长方体的六个面涂上红色,然后把这个长方体切割成棱长为1cm的小正方体。这些小正方体中恰好有两个面涂上红色的有多少个?
19.如图,是一个长为5厘米,宽为4厘米、高为3厘米的长方体,在它的表面涂上颜色后再截成棱长为1厘米的小正方体,其中三面、两面和一面被涂色的小正方体有多少个?
20.一个大正方体,先在它的每个面上都涂上红色,再把它切成棱长是的小正方体。已知两面涂色的小正方体有96个,原来大正方体的体积是多少立方厘米?
21.一个长方体木块(如图),长是,宽是,高是,先在它的六个面上都涂上色,然后把它锯成棱长都是
的小正方体木块。在锯成的小正方体木块中,三面涂色的有多少块?两面、一面涂色的各有多少块?六个面都没有涂色的有多少块?
参考答案:
1.B
【详解】
拿走一个小正方体后表面积等于原来拼成的大正方体的表面积;
故答案为:B。
2.A
【详解】
仔细观察由27个小正方体组成的大正方体,三面涂色的小正方体在顶点处,因为有8个顶点,所以有8个这样的小正方体。
故答案为A。
3.B
【详解】
该立体图形由7+5+1=13(个)个小立方体组成的
故答案为:B
4.D
【详解】
由分析可知只有长方体两端的两个小正方体是5个面涂色,如下图:(图形不唯一)
故答案为:D。
5.C
【详解】
根据分析,中间只有1个小正方体,正方体有6个面,一面涂色的有6个;有12条棱,两面涂色的有12个;有8个顶点,三面涂色的有8个。
故答案为:C
6.C
【详解】
2÷1=2(个)
2×2×2=8(个)
故答案为:C。
7.B
【详解】
根据分析可得:
一面涂色:(3-2)×(3-2)×6
=1×1×6
=6(个)
两面涂色:(3-2)×12
=1×12
=12(个)
三面涂色:8个
故答案为:B。
8.C
【详解】
因为3面图色的在8个顶点上,所以一共有8个。
故答案为:C
9.D
【详解】
A.(3+3+3)×(7×7)
=9×49
=441(平方厘米);
B.(4+2+3)×(7×7)
=9×49
=441(平方厘米);
C.(4+3+2)×(7×7)
=9×49
=441(平方厘米);
D.(2+2+4)×(7×7)
=8×49
=392(平方厘米)
故答案为:D。
10.C
【详解】
24÷5=4(组) 4(个),说明第24个图形应该是第5组中的第4个,即是□。
故答案为:C
11.A
【详解】
如图中一个长方体被挖掉一小块,体积减少,表面积不变。
故答案为:A
12.D
【详解】
由图可知图形时按圆形、三角形、正方形、心形循环排列的,每四个图形一循环,因为16÷4=4,所以16个图形为心形.
13.C
【详解】
(10×10)×(6+5+6),
=100×17
=1700(厘米2)
答:露在外面的面积是1700厘米2.
故选C
14. 8 8
【详解】
由分析可知:三面涂色的有8个;没有涂色的有(4-2)×(4-2)×(4-2)=8个。
15.54;90;126;51
【详解】
试题分析:每个正方体的棱长都是3厘米,则每个小正方形面的面积都是32平方厘米;所以1个正方体的表面积是6×32平方厘米,可以写成(2+4)×32平方厘米,
2个正方体拼组后减少了两个面,所以表面积是10×32平方厘米;可以写成(2+2×4)×32平方厘米,
3个正方体拼组在一起减少了4个面,表面积是14×32平方厘米,可以写成(2+3×4)×32平方厘米,
所以每增加一个小正方体就增加了4个面…
由此若是n个正方体拼组一起表面积就可以写成(2+n×4)×32平方厘米,由此即可解决问题.
解:1个正方体的表面积是(2+4)×32=54平方厘米;
2个正方体的表面积是(2+2×4)×32=90平方厘米;
3个正方体的表面积是(2+3×4)×32=126平方厘米;
(2+n×4)×32=1854,
(2+n×4)×9=1854,
2+n×4=206,
n×4=204,
n=51.
答:1个正方体的表面积是54平方厘米;2个正方体的表面积是90平方厘米;3个正方体的表面积是126平方厘米;51个面积是1854平方厘米.
故答案为54;90;126;51.
16.(1)14;13;(2)46;(3).
【详解】
试题分析:(1)观察图形可知:最下面一行中有3×3=9个小正方体,中间一行中有4个小正方体,上面一行只有1个小正方体;可以组成的正方体的棱长最少是3个小正方体的棱长,由此可以求得需要的小正方体的总个数解决问题;
(2)上下面看到的正方体的面有3×3=9个面;前后、左右看到的小正方体的面都是3+3+1=7个面;
(3)从右边看到的图形是:下面3个正方形,中间3个正方形,上面1个正方形.
解:(1)图形中小正方体的个数为:9+4+1=14(个),
组成一个大正方体至少还需要小正方体的个数为:3×3×3﹣14=27﹣14=13(个),
(2)1×1×(9×2+7×4),
=1×46,
=46(平方厘米),
答:这个图形的表面积是46平方厘米;
(3)从右边看这图形的形状是:
故答案为(1)14;13;(2)46;(3).
17.6
【详解】
由分析可知:有四个面涂色的正方体上层有2个,下层有4个,共6个。
18.12个
【详解】
2×4+1×4=12(个)
19.8个;24个;22个
【详解】
长方体有8个顶点,所以三面被涂色的小正方体有8个。
长方体有12条棱,其中每条长上有3个小正方体,宽上有2个小正方体,高上有1个小正方体,所以两面被涂色的小正方体有:(3+2+1)×4=24(个)。
长方体有6个面,前面和后面,每个面上中间部分的小正方体有3个;左面和右面,每个面上中间部分的小正方体有2个;上面和下面,每个面上中间部分的小正方体有6个,所以一面被涂色的小正方体有:(3+2+6)×2=22(个)。
答:三面被涂色的小正方体有8个,两面被涂色的小正方体有24个,一面被涂色的小正方体有22个。
20.
【详解】
(个)
答:原来大正方体的体积是。
21.在锯成的小正方体木块中,三面涂色的有8块,两面涂色的有24块,一面涂色的有22块,六个面都没有涂色的有6块。
【详解】
由分析得:
三面涂色的有:1×8=8(块)
两面涂色的有:
(块)
一面涂色的有:
(块)
(块)
