华东师大版八年级下册数学19.2.2 菱形的判定课件 (共14张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学19.2.2 菱形的判定课件 (共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 275.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 00:00:00 | ||
图片预览



文档简介
(共14张PPT)
菱形的判定
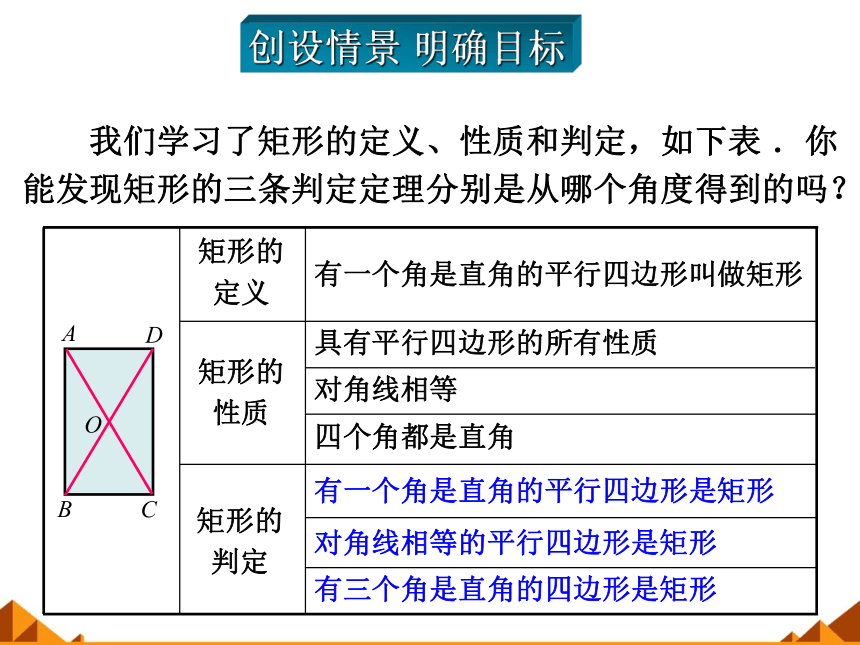
我们学习了矩形的定义、性质和判定,如下表 .你
能发现矩形的三条判定定理分别是从哪个角度得到的吗?
矩形的
定义
有一个角是直角的平行四边形叫做矩形
矩形的
性质
具有平行四边形的所有性质
对角线相等
四个角都是直角
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
C
D
A
B
O
矩形的
判定
创设情景 明确目标
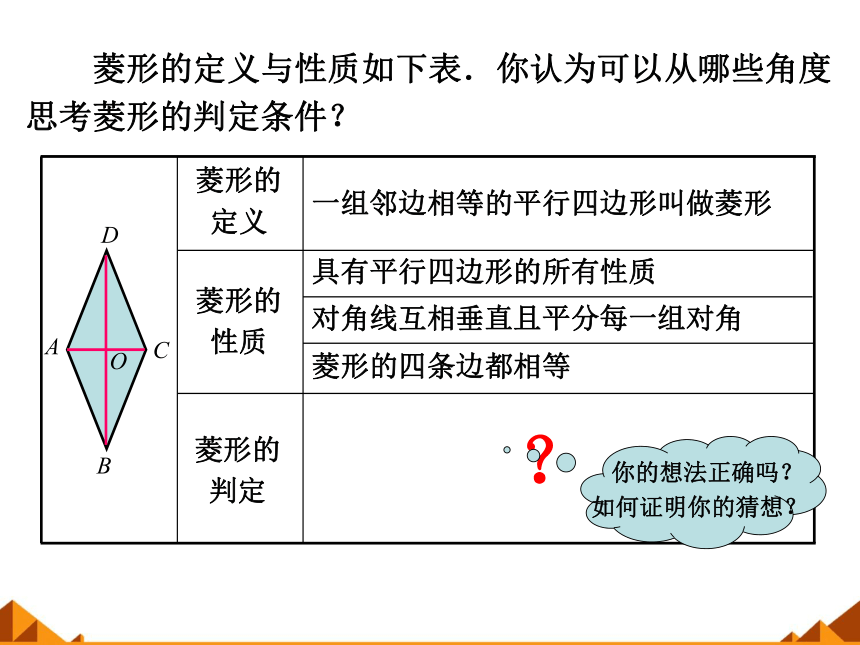
菱形的定义与性质如下表.你认为可以从哪些角度
思考菱形的判定条件?
菱形的
定义
一组邻边相等的平行四边形叫做菱形
菱形的
性质
具有平行四边形的所有性质
对角线互相垂直且平分每一组对角
菱形的四条边都相等
菱形的
判定
C
D
A
B
O
?
你的想法正确吗?
如何证明你的猜想?
1.掌握菱形的三种判定方法,能根据不同的已知条
件,选择适当的判定定理进行推理和计算;
2.经历菱形判定定理的探究过程,渗透类比思想,
体会研究图形判定的一般思路.
定理1:对角线互相垂直的平行四边形是菱形。
探究点一 菱形的判定
求证:对角线互相垂直的平行四边形是菱形。
如图, ABCD中,对角线AC,BD相交于点O,且
AC⊥BD.求证: ABCD是菱形。
B
C
A
D
O
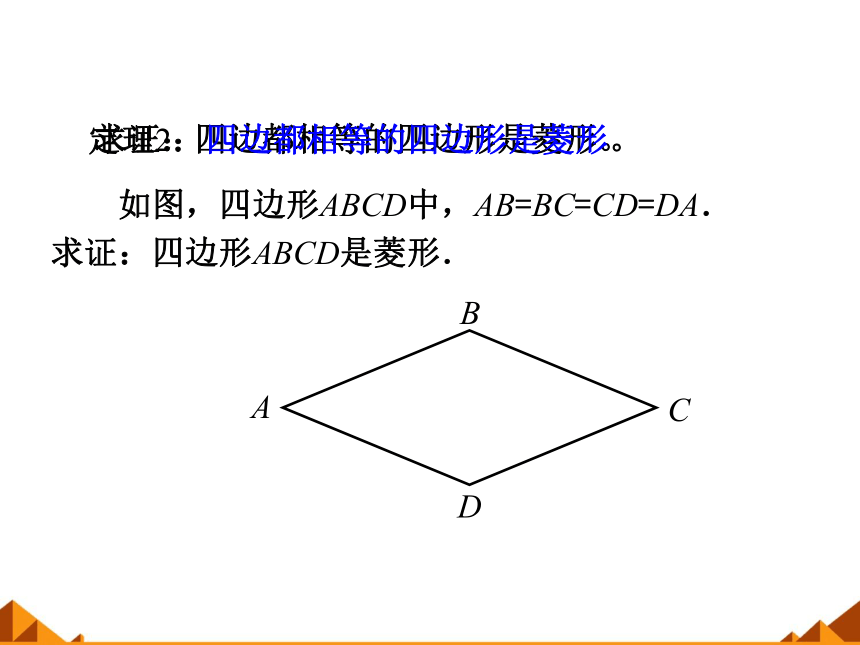
求证:四边都相等的四边形是菱形。
如图,四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.
D
C
A
B
定理2:四边都相等的四边形是菱形。
?
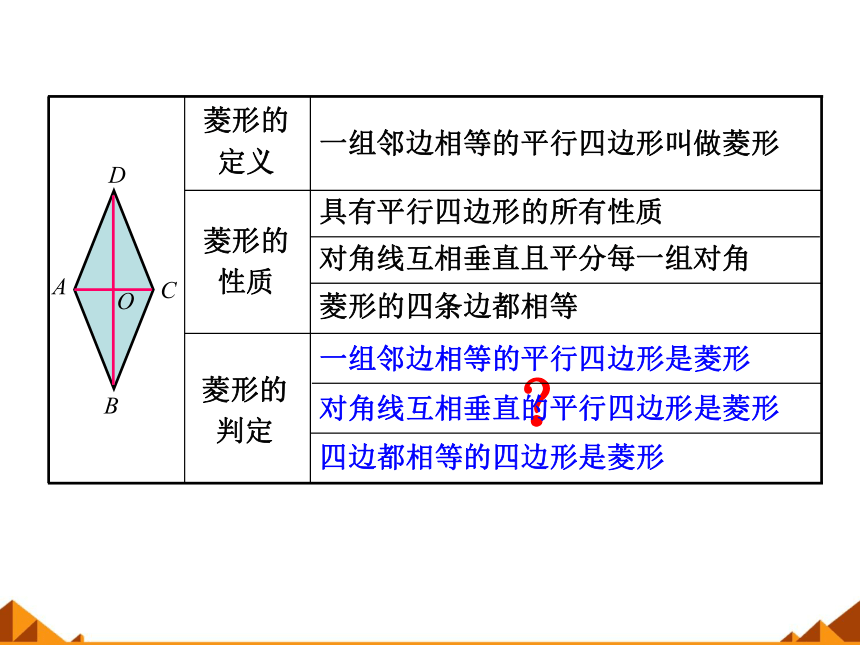
菱形的
定义
一组邻边相等的平行四边形叫做菱形
菱形的
性质
具有平行四边形的所有性质
对角线互相垂直且平分每一组对角
菱形的四条边都相等
菱形的
判定
C
D
A
B
O
一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四边都相等的四边形是菱形
A
B
C
D
O
菱形
证明:∵四边形ABCD是平行四边形,
∴A0= _ ,
又∵AC⊥BD,
∴AB=BC,(线段垂直平分线上的点_________
______________)
∴ ABCD是菱形.(菱形的定义)
⊥
CO
到两个端
点的距离相等
已知:如图,在 ABCD中,AC BD,
求证: ABCD是 .
探究点二 菱形的判定的运用
如图,AD平分∠BAC,DE∥AC交AB于点E,
DF∥AB交AC于点F.求证:四边形AEDF是菱形。
A
B
C
D
E
F
三个角是直角
四条边都相等
一个角是直角
对角线相等
一组邻边相等
对角线互相垂直
两组对边分别平行
一组对边平行且相等
两组对边分别相等
两组对角分别相等
对角线互相平分
四边形
平行四边形
矩形
菱形
总结梳理 内化目标
1、一边长为5cm的平行四边形,两条对角线的长分别为6cm和8cm,那么平行四边形的面积是
.
2、菱形的两条对角线长分别是3和4,则周长和面积分别是 ,
3、菱形周长为80,一对角线为20,则较小的角的度数为____ 、面积为_____ .
24
10cm
6
60°
c㎡
c㎡
达标检测 反思目标
4、如图,用一长一短两根木条,在它们的中点处固定一个小钉,做成一个可转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?请说明理由。
达标检测 反思目标
A
B
C
D
5、如图,先画两条等长的线段AB,AD,然后分别
以B,D为圆心,AB长为半径画弧,两弧交点为C,连接
BC,CD.得到的四边形ABCD是菱形吗?请说明理由。
F
A
B
C
D
E
O
6 如图, ABCD的对角线AC的垂直平分线与
AD,BC分别交于点E,F.求证:四边形AFCE是菱形。
菱形的判定
我们学习了矩形的定义、性质和判定,如下表 .你
能发现矩形的三条判定定理分别是从哪个角度得到的吗?
矩形的
定义
有一个角是直角的平行四边形叫做矩形
矩形的
性质
具有平行四边形的所有性质
对角线相等
四个角都是直角
有一个角是直角的平行四边形是矩形
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
C
D
A
B
O
矩形的
判定
创设情景 明确目标
菱形的定义与性质如下表.你认为可以从哪些角度
思考菱形的判定条件?
菱形的
定义
一组邻边相等的平行四边形叫做菱形
菱形的
性质
具有平行四边形的所有性质
对角线互相垂直且平分每一组对角
菱形的四条边都相等
菱形的
判定
C
D
A
B
O
?
你的想法正确吗?
如何证明你的猜想?
1.掌握菱形的三种判定方法,能根据不同的已知条
件,选择适当的判定定理进行推理和计算;
2.经历菱形判定定理的探究过程,渗透类比思想,
体会研究图形判定的一般思路.
定理1:对角线互相垂直的平行四边形是菱形。
探究点一 菱形的判定
求证:对角线互相垂直的平行四边形是菱形。
如图, ABCD中,对角线AC,BD相交于点O,且
AC⊥BD.求证: ABCD是菱形。
B
C
A
D
O
求证:四边都相等的四边形是菱形。
如图,四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形.
D
C
A
B
定理2:四边都相等的四边形是菱形。
?
菱形的
定义
一组邻边相等的平行四边形叫做菱形
菱形的
性质
具有平行四边形的所有性质
对角线互相垂直且平分每一组对角
菱形的四条边都相等
菱形的
判定
C
D
A
B
O
一组邻边相等的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
四边都相等的四边形是菱形
A
B
C
D
O
菱形
证明:∵四边形ABCD是平行四边形,
∴A0= _ ,
又∵AC⊥BD,
∴AB=BC,(线段垂直平分线上的点_________
______________)
∴ ABCD是菱形.(菱形的定义)
⊥
CO
到两个端
点的距离相等
已知:如图,在 ABCD中,AC BD,
求证: ABCD是 .
探究点二 菱形的判定的运用
如图,AD平分∠BAC,DE∥AC交AB于点E,
DF∥AB交AC于点F.求证:四边形AEDF是菱形。
A
B
C
D
E
F
三个角是直角
四条边都相等
一个角是直角
对角线相等
一组邻边相等
对角线互相垂直
两组对边分别平行
一组对边平行且相等
两组对边分别相等
两组对角分别相等
对角线互相平分
四边形
平行四边形
矩形
菱形
总结梳理 内化目标
1、一边长为5cm的平行四边形,两条对角线的长分别为6cm和8cm,那么平行四边形的面积是
.
2、菱形的两条对角线长分别是3和4,则周长和面积分别是 ,
3、菱形周长为80,一对角线为20,则较小的角的度数为____ 、面积为_____ .
24
10cm
6
60°
c㎡
c㎡
达标检测 反思目标
4、如图,用一长一短两根木条,在它们的中点处固定一个小钉,做成一个可转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?请说明理由。
达标检测 反思目标
A
B
C
D
5、如图,先画两条等长的线段AB,AD,然后分别
以B,D为圆心,AB长为半径画弧,两弧交点为C,连接
BC,CD.得到的四边形ABCD是菱形吗?请说明理由。
F
A
B
C
D
E
O
6 如图, ABCD的对角线AC的垂直平分线与
AD,BC分别交于点E,F.求证:四边形AFCE是菱形。
