华东师大版八年级下册数学18.2 从角、对角线的角度判定平行四边形(1) 教案
文档属性
| 名称 | 华东师大版八年级下册数学18.2 从角、对角线的角度判定平行四边形(1) 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 57.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 07:31:08 | ||
图片预览

文档简介
平行四边形判定
学习目标:1、探索判定平行四边形所需的条件。
2、掌握综合运用平行四边形性质定理和判定定理解决相关问题。
学习重点:探索判定平行四边形所需的条件
学习难点:掌握综合运用平行四边形性质定理和判定定理解决相关问题。
学习程序:
一、温故而知新
说说你学过的平行四边形的判定有哪些?
二、探索与交流
1.作一个两条对角线互相平分的四边形
(可以参考课本85页)
2.观察你和你的同伴所作的四边形是平行四边形吗?
3.尝试用演绎推理证明你的结论。
对角线互相平分的四边形是平行四边形
已知:(如图)在四边形ABCD中,对角线AC和BD相交于点O,OA=OC,OB=OD
求证:四边形ABCD是平行四边形
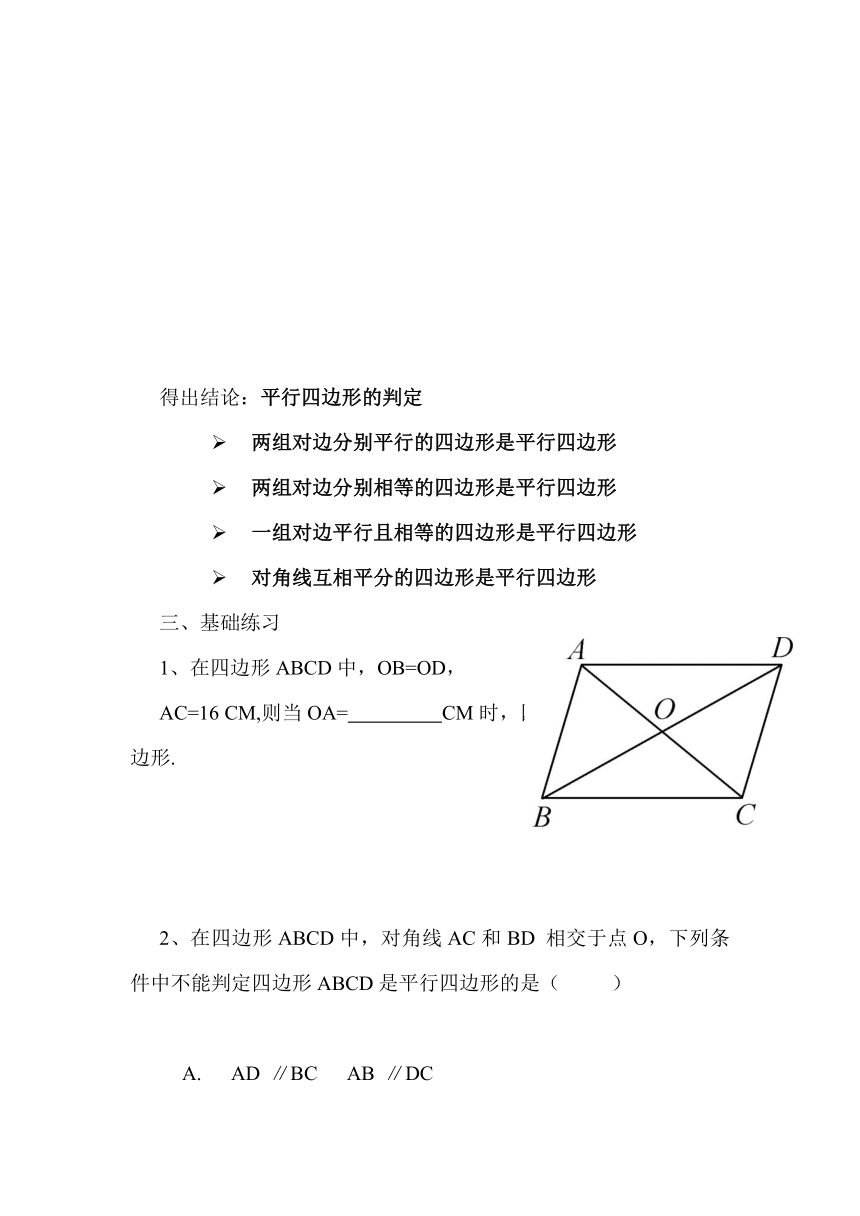
得出结论:平行四边形的判定
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
三、基础练习
1、在四边形ABCD中,OB=OD,
AC=16 CM,则当OA= CM时,四边形ABCD是平行四边形.
2、在四边形ABCD中,对角线AC和BD 相交于点O,下列条件中不能判定四边形ABCD是平行四边形的是( )
A. AD ∥BC AB ∥DC
B. AD =BC AB =DC
C OA=OC OB=OD
D. AB ∥DC AD =BC
3、如图:AD为三角形ABC的中线,AB=9,
AC=12,延长AD至点E,使DE=AD,
连接BE\CE,则四边形ABEC的周长是
4、 如图:反比例函数图象与正比例函数y=k1x和y=k2x的图象有四个交点,则顺次连结这四个点所构成的四边形的形状是
开放探究题
如图,已知四边形ABCD的对角形
AC、BD相交于点O,给出下列5个条件:
(1)AB ∥DC (2)OA=OC (3)AB=DC
(4)∠BAD= ∠ DCB (5) AD ∥BC
(1)从以上5个条件中任意选取哪2个条件,可推出四边形ABCD是平行四边形,并说明理由;
(2)对由以上5个条件中任意选取2个条件,不能推出四边形ABCD是平行四边形的,请选取一种情形举例说明.
四、课堂小结:谈谈本节收获
五、课后作业;
学习目标:1、探索判定平行四边形所需的条件。
2、掌握综合运用平行四边形性质定理和判定定理解决相关问题。
学习重点:探索判定平行四边形所需的条件
学习难点:掌握综合运用平行四边形性质定理和判定定理解决相关问题。
学习程序:
一、温故而知新
说说你学过的平行四边形的判定有哪些?
二、探索与交流
1.作一个两条对角线互相平分的四边形
(可以参考课本85页)
2.观察你和你的同伴所作的四边形是平行四边形吗?
3.尝试用演绎推理证明你的结论。
对角线互相平分的四边形是平行四边形
已知:(如图)在四边形ABCD中,对角线AC和BD相交于点O,OA=OC,OB=OD
求证:四边形ABCD是平行四边形
得出结论:平行四边形的判定
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
三、基础练习
1、在四边形ABCD中,OB=OD,
AC=16 CM,则当OA= CM时,四边形ABCD是平行四边形.
2、在四边形ABCD中,对角线AC和BD 相交于点O,下列条件中不能判定四边形ABCD是平行四边形的是( )
A. AD ∥BC AB ∥DC
B. AD =BC AB =DC
C OA=OC OB=OD
D. AB ∥DC AD =BC
3、如图:AD为三角形ABC的中线,AB=9,
AC=12,延长AD至点E,使DE=AD,
连接BE\CE,则四边形ABEC的周长是
4、 如图:反比例函数图象与正比例函数y=k1x和y=k2x的图象有四个交点,则顺次连结这四个点所构成的四边形的形状是
开放探究题
如图,已知四边形ABCD的对角形
AC、BD相交于点O,给出下列5个条件:
(1)AB ∥DC (2)OA=OC (3)AB=DC
(4)∠BAD= ∠ DCB (5) AD ∥BC
(1)从以上5个条件中任意选取哪2个条件,可推出四边形ABCD是平行四边形,并说明理由;
(2)对由以上5个条件中任意选取2个条件,不能推出四边形ABCD是平行四边形的,请选取一种情形举例说明.
四、课堂小结:谈谈本节收获
五、课后作业;
