2.3查理定律和盖—吕萨克定律课后练习-2021-2022学年高二下学期物理沪教版(2019)选择性必修第三册(word 含答案)
文档属性
| 名称 | 2.3查理定律和盖—吕萨克定律课后练习-2021-2022学年高二下学期物理沪教版(2019)选择性必修第三册(word 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 240.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-21 00:00:00 | ||
图片预览



文档简介
2.3查理定律和盖—吕萨克定律
一、选择题(共15题)
1.夏天开空调,冷气从空调中吹进室内,则室内气体分子的
A.热运动剧烈程度加剧
B.平均动能变大
C.每个分子速率都会相应的减小
D.速率小的分子数所占的比例升高
2.一根两端封闭粗细均匀的直玻璃中有一段长57厘米的水银柱,在水银柱两边各有一段空气柱(如图).当玻璃管水平放置,两段空气柱长度均为30厘米,压强都是一个标准大气压,现将玻璃管缓慢竖立起来,则上下两段空气柱的长度分别为( )
A.30厘米,30厘米
B.35厘米,25厘米
C.40厘米,20厘米
D.45厘米,15厘米
3.压强的微观原因是气体分子对容器壁的作用,关于气体的压强,下列说法正确的是( )
A.气体压强的大小只与分子平均动能有关
B.单位体积内的分子数越多,分子平均速率越大,压强就越大
C.一定质量的气体,体积越小,温度越高,压强就越小
D.气体膨胀对外做功且温度降低,气体的压强可能不变
4.负压病房是收治传染性极强的呼吸道疾病病人所用的医疗设施,可以大大减少医务人员被感染的机会,病房中气压小于外界环境的大气压。若负压病房的温度和外界温度相同,负压病房内气体和外界环境中气体都可以看成理想气体,则以下说法正确的是( )
A.负压病房内气体分子的平均速率小于外界环境中气体分子的平均速率
B.负压病房内每个气体分子的运动速率都小于外界环境中每个气体分子的运动速率
C.负压病房内单位体积气体分子的个数小于外界环境中单位体积气体分子的个数
D.相同面积下,负压病房内壁受到的气体压力等于外壁受到的气体压力
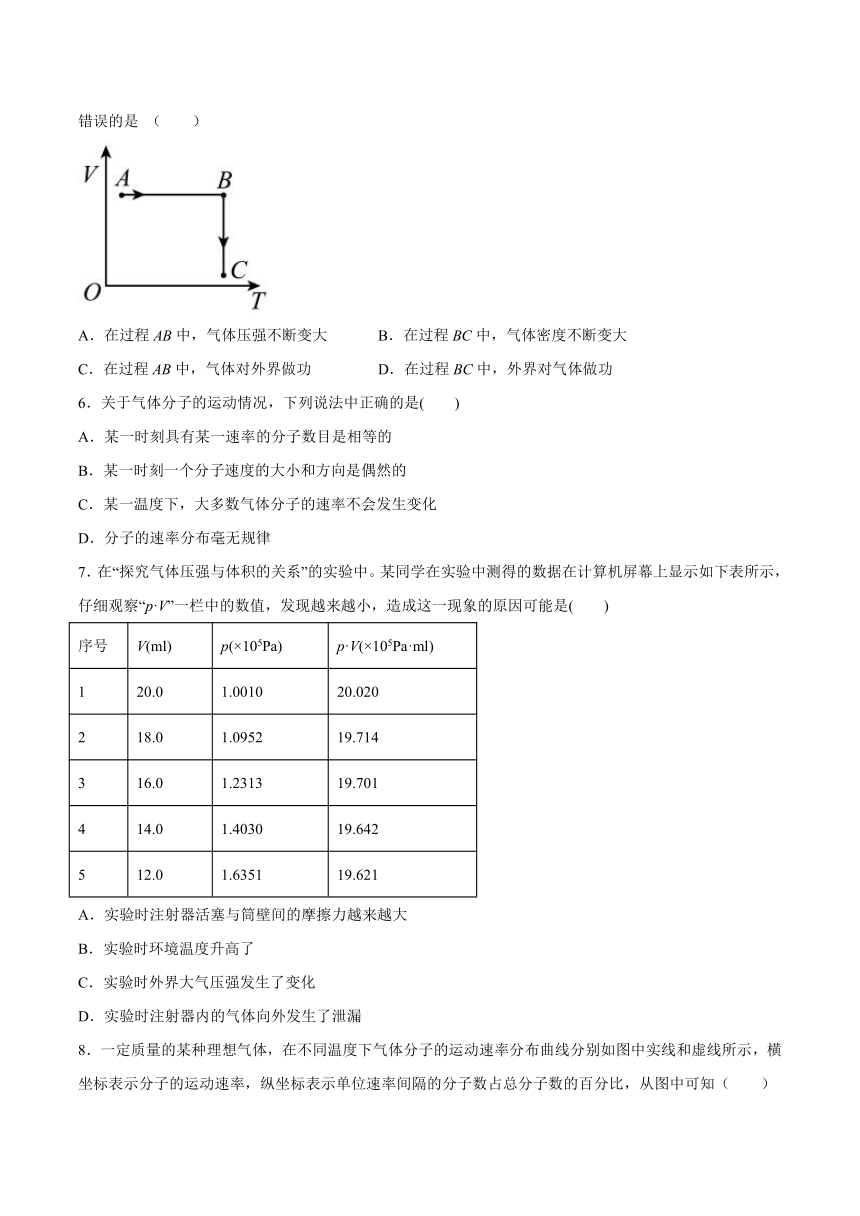
5.一定质量的理想气体自状态A经状态B变化到状态C,这一过程在V-T图中表示如图所示,则下述结论错误的是 ( )
A.在过程AB中,气体压强不断变大 B.在过程BC中,气体密度不断变大
C.在过程AB中,气体对外界做功 D.在过程BC中,外界对气体做功
6.关于气体分子的运动情况,下列说法中正确的是( )
A.某一时刻具有某一速率的分子数目是相等的
B.某一时刻一个分子速度的大小和方向是偶然的
C.某一温度下,大多数气体分子的速率不会发生变化
D.分子的速率分布毫无规律
7.在“探究气体压强与体积的关系”的实验中。某同学在实验中测得的数据在计算机屏幕上显示如下表所示,仔细观察“p·V”一栏中的数值,发现越来越小,造成这一现象的原因可能是( )
序号 V(ml) p(×105Pa) p·V(×105Pa·ml)
1 20.0 1.0010 20.020
2 18.0 1.0952 19.714
3 16.0 1.2313 19.701
4 14.0 1.4030 19.642
5 12.0 1.6351 19.621
A.实验时注射器活塞与筒壁间的摩擦力越来越大
B.实验时环境温度升高了
C.实验时外界大气压强发生了变化
D.实验时注射器内的气体向外发生了泄漏
8.一定质量的某种理想气体,在不同温度下气体分子的运动速率分布曲线分别如图中实线和虚线所示,横坐标表示分子的运动速率,纵坐标表示单位速率间隔的分子数占总分子数的百分比,从图中可知( )
A.虚线对应的温度高 B.实线对应的分子平均动能大
C.相同体积下,虚线对应的气体压强大 D.相同压强下,实线对应的气体密度大
9.下列说法中正确的是
A.布朗运动反映了固体微粒中的分子运动的无规则性
B.对不同种类的物体,只要温度相同,分子的平均动能一定相同
C.分子间距离增大时,分子间的引力增大而斥力减小
D.一定质量的气体,温度升高时,分子间的平均距离一定增大
10.如图所示,一个横截面积为S的圆筒形容器竖直放置。金属圆板形活塞的下表面是水平的,上表面是倾斜的,上表面与水平面的夹角为θ,圆板的质量为M。不计圆板与容器内壁之间的摩擦。若大气压强为p0,则被圆板封闭在容器中的气体的压强p等于( )
A. B. C. D.
11.一定质量的理想气体,保持体积不变,压强减为原来的一半,则其温度由原来的27℃变为( )
A.127K B.150K C.13.5℃ D.-23.5℃
12.如图所示为某种一定质量的理想气体,由初态a经不同过程到达终态b,则关于a、b两点压强下列判断中正确的是( )
A. B. C. D.不能确定
13.活塞可以在气缸内自由移动,缸内贮有一定质量的理想气体,则气体可能发生的状态变化是( )
A.温度升高,压强减小,体积减小 B.温度降低,压强增大,体积减小
C.温度升高,压强减小,密度减小 D.温度降低,压强增大,密度不变
14.下面关于气体压强的说法正确的是( )
A.气体对器壁产生的压强是由于大量气体分子频繁碰撞器壁而产生的
B.气体对器壁产生的压强等于作用在器壁单位面积上的平均作用力
C.从微观角度看,气体压强的大小跟气体分子的平均动能和分子密集程度有关
D.从宏观角度看,气体压强的大小跟气体的温度和体积有关
15.如图所示,导热的汽缸固定在水平地面上,用活塞把一定质量的理想气体封闭在汽缸中,汽缸的内壁光滑.现用水平外力F作用于活塞杆,使活塞缓慢地向右移动,由状态①变化到状态②,在此过程中如果环境保持恒温,下列说法正确的是 ( )
A.每个气体分子的速率都不变
B.气体分子平均动能不变
C.水平外力F逐渐变大
D.气体内能减小
二、填空题
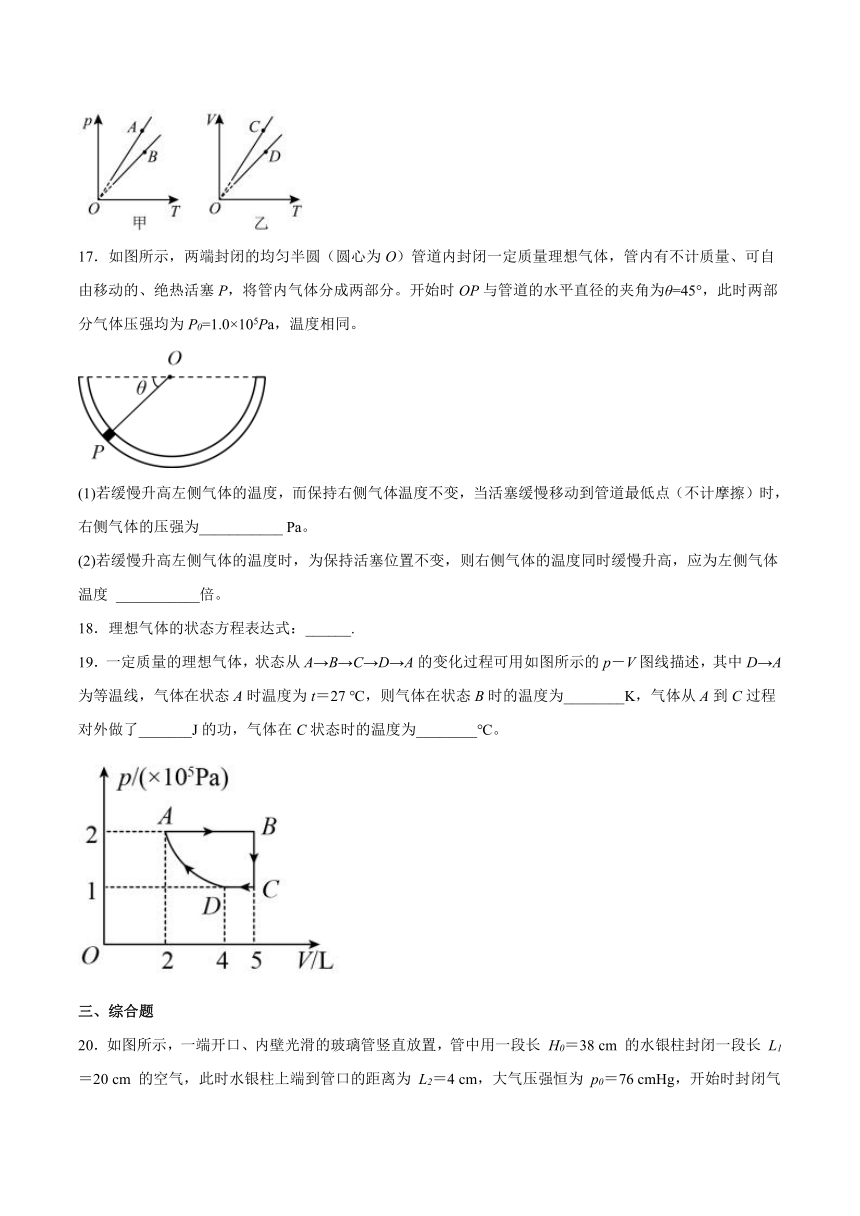
16.对于一定质量的理想气体,以p、V、T三个状态参量中的两个为坐标轴建立直角坐标系,在坐标系上描点能直观地表示这两个参量的数值.如图所示,两个坐标系中,两个点都表示相同质量某种理想气体的两个状态。根据坐标系中不同点的位置来比较第三个参量的大小。
(1)p T图象(图甲)中A、B两个状态,________状态体积小;
(2)V T图象(图乙)中C、D两个状态,________状态压强小。
17.如图所示,两端封闭的均匀半圆(圆心为O)管道内封闭一定质量理想气体,管内有不计质量、可自由移动的、绝热活塞P,将管内气体分成两部分。开始时OP与管道的水平直径的夹角为θ=45°,此时两部分气体压强均为P0=1.0×105Pa,温度相同。
(1)若缓慢升高左侧气体的温度,而保持右侧气体温度不变,当活塞缓慢移动到管道最低点(不计摩擦)时,右侧气体的压强为___________ Pa。
(2)若缓慢升高左侧气体的温度时,为保持活塞位置不变,则右侧气体的温度同时缓慢升高,应为左侧气体温度 ___________倍。
18.理想气体的状态方程表达式:______.
19.一定质量的理想气体,状态从A→B→C→D→A的变化过程可用如图所示的p-V图线描述,其中D→A为等温线,气体在状态A时温度为t=27 ℃,则气体在状态B时的温度为________K,气体从A到C过程对外做了_______J的功,气体在C状态时的温度为________℃。
三、综合题
20.如图所示,一端开口、内壁光滑的玻璃管竖直放置,管中用一段长 H0=38 cm 的水银柱封闭一段长 L1=20 cm 的空气,此时水银柱上端到管口的距离为 L2=4 cm,大气压强恒为 p0=76 cmHg,开始时封闭气体温度为 t1=27 ℃,取 0 ℃为 273 K.求:
(1)缓慢升高封闭气体温度至水银开始从管口溢出,此时封闭气体的温度;
(2)保持封闭气体初始温度 27 ℃不变,在竖直平面内从图示位置缓慢转动至玻璃管水平
过程中,求从管口溢出的水银柱的长度.(转动过程中没有发生漏气)
21.如图所示,一活塞将一定质量的理想气体封闭在固定导热汽缸内,活塞可沿汽缸无摩擦地滑动,活塞横截面积为,质量不计。开始时活塞距离汽缸底部为,外界大气压强,环境温度为℃。
(1)当环境温度缓慢升高至57℃时,活塞距离汽缸底部的距离为多少?
(2)当环境温度升高至57℃时,为使活塞距离汽缸底部的距离仍为,可对活塞施加一水平向左的推力F使活塞处于平衡状态,求推力F应为多大?
22.一定质量的空气,27℃时的体积为1.0×10-2m3,在压强不变的情况下,温度升高到127℃时体积是多大?
23.如图所示,粗细均匀、横截面积相等的U形管竖直放置,左管上端封闭,右管上端开口,两管高度均为。右管中有高的水银柱,水银柱上表面离管口的距离,管底水平段的体积可忽略。环境温度为。大气压强。现将型管水平放置,使左右两管均在同一水平面上。求∶
(1)此时水银柱与大气相通的表面到管口的距离;
(2)再将环境温度缓慢升高,使水银柱与大气相通的表面恰好与管口相平时的环境温度。
试卷第1页,共3页
参考答案:
1.D
【详解】
试题分析:冷气从空调中吹进室内,室内温度减小,分子热运动剧烈程度减小,分子平均动能减小,即速率小的分子数所占的比例升高,但不是每个分子的速率都减小,D正确.
2.C
【详解】
,
设左侧气体参数为
,
右侧气体为
,
根据理想气体状态方程
联立上述方程可以求得
3.B
【详解】
A.气体压强的大小与分子平均动能和分子的数密度有关,故A错误;
B.单位体积内的分子数越多,分子平均速率越大,压强就越大,故B正确;
C.一定质量的气体,体积越小,温度越高,压强就越大,故C错误;
D.根据理想气体状态方程可知,气体膨胀对外做功且温度降低,气体的压强一定变小,故D错误。
故选B。
4.C
【详解】
A.负压病房的温度和外界温度相同,故负压病房内气体分子的平均速率等于外界环境中气体分子的平均速率,故A错误;
B.负压病房内气体分子的平均运动速率相等,故不可能负压病房内每个气体分子的运动速率都小于外界环境中每个气体分子的运动速率,故B错误;
C.决定气体压强的微观因素:单位体积气体分子数和气体分子的平均速率,现内外温度相等,即气体分子平均速率相等,压强要减小形成负压,则要求负压病房内单位体积气体分子的个数小于外界环境中单位体积气体分子的个数,故C正确;
D.压力,内外压强不等,相同面积下,负压病房内壁受到的气体压力小于外壁受到的气体压力,故D错误。
故选C。
5.C
【详解】
C.在过程AB中,为等容变化,气体对外界做功为零,所以C项正确;
A.根据理想气体状态方程,温度升高过程中压强增大,所以A项错误;
D.在过程BC中,为等温变化,体积减小,外界对气体做功,D项错误;
B.一定质量的气体,体积减小,密度增大,B项错误。
故选C。
6.B
【详解】
AD.具有某一速率的分子数目并不是相等的,呈“中间多,两头少”的统计规律分布,故AD错误;
B.由于分子之间不断地碰撞,分子随时都会改变自己的运动情况,因此在某一时刻,一个分子速度的大小和方向完全是偶然的,故B正确;
C.某一温度下,每个分子的速率仍然是随时变化的,只是分子运动的平均速率不变,故C错误。
故选B。
7.D
【详解】
A.实验时注射器活塞与筒壁间的摩擦力不断增大,不会影响气压与体积,故A错误;
B.实验时环境温度增大了,根据理想气体状态方程
PV乘积变大,故B错误;
C.封闭气体压强与外界大气压强无关,故C错误;
D.实验时注射器的空气向外发生了泄漏,根据理想气体状态方程
常数C与质量有关,变小,故PV乘积减小,故D正确;
故选D。
8.B
【详解】
AB.由图可知图中实线对应的速率较大,由于温度越高,速率大的分子占的比例越大,则实线对应的气体分子温度较高,温度是平均动能的标志,图中实线对应的温度高,则分子平均动能大,故B正确,A错误;
C.由理想气体状态方程
可得相同体积下,实线对应的气体压强大,故C错误;
D.由
联立可得
可得质量相同,压强相同,温度越高,密度越小,故D错误。
故选B。
9.B
【详解】
A:布朗运动反映了液体中分子运动的无规则性.故A项错误.
B:温度是分子平均动能的标志,对不同种类的物体,只要温度相同,分子的平均动能一定相同.故B项正确.
C:分子间距离增大时,分子间的引力、斥力均减小.故C项错误.
D:一定质量的气体,温度升高时,压强如果同时也有变化,则气体体积的变化不能确定,因而气体分子间的平均距离不一定增大.故D项错误.
10.D
【详解】
以活塞为研究对象,分析受力有:重力Mg、外界大气压力p0S,气缸壁的压力N和缸内气体的压力F,受力分析图如下
其中
F = p
根据平衡条件得
p0S + mg = Fcosθ
联立求解得
p = p0 +
故选D。
11.B
【详解】
根据气体做等容变化有
则压强减为原来的一半时,热力学温度也减为原来的一半,则有
所以B正确;ACD错误;
故选B。
12.C
【详解】
根据理想气体状态方程有
由此可得图像的斜率,即斜率越大,压强越小,如图所示
所以有,故选C。
13.BC
【详解】
AC.根据
可知,温度升高,压强减小,体积必然要增大,密度减小,选项A错误,C正确;
BD.根据
可知,温度降低,压强增大,体积减小,密度增大,选项B正确,D错误;
故选BC。
14.ABCD
【详解】
A.气体对器壁产生的压强是由于大量气体分子频繁碰撞器壁而产生的,选项A正确;
B.气体对器壁产生的压强等于作用在器壁上单位面积的平均作用力,选项B正确;
C.从微观角度看,气体压强的大小跟气体分子的平均动能和分子密集程度有关,分子平均动能越大,则分子撞击器壁的作用力越大,压强越大;分子密度越大,则单位时间撞击器壁单位面积上的分子数越多,则压强越大,选项C正确;
D.从宏观的角度看,温度越高,分子的平均速率越大,分子的平均动能越大,体积越小,单位时间内的气体分子数越多,分子对器壁的碰撞越频繁,气体对器壁的压强就越大,否则压强就越小,选项D正确。
故选ABCD。
15.BC
【详解】
试题分析:封闭气体等温膨胀过程,温度是分子热运动平均动能的标志,故分子热运动的平均动能不变,不是每个分子动能都不变,所以A错误;气体等温膨胀,温度不变,则气体分子的平均动能不变,B正确;温度不变,体积增大,根据,则压强P减小,以活塞为研究对象,根据平衡条件:,得:,压强P减小,则F增大,C正确;理想气体的内能只与温度有关,温度不变,则内能不变,故D错误.
16. A C
【详解】
甲图画出的倾斜直线为等容线,斜率越小,体积越大,所以VB>VA。
乙图画出的倾斜直线为等压线,斜率越小,压强越大,所以pD>pC。
17. 1.5×105 1
【详解】
(1)对于管道右侧气体,由于气体做等温变化,则有:
p0V1=p2V2
解得
p2=1.5×105Pa
(2)左右两边气体的体积均不变,则对左侧气体
对右侧气体
p左=p右
则
T左=T右
即右侧气体的温度应为左侧气体温度1倍。
18. =C.
19. 750 6×105 102
【详解】
A到B过程气体做等压变化,则
TA=27 ℃+273 K=300 K
解得
TB=750 K
从A到B过程气体对外界做功
W=pΔV=6×105 J
从B到C过程体积不变,所以外界对气体不做功,所以气体从A到C过程气体对外界做功为6×105 J;
气体在C状态压强为B时的一半,则温度也为B时的一半,即
tC=375 K=102 ℃
20.(1)87 ℃;(2)6cm
【详解】
试题分析:(1)设玻璃管横截面积为 S,初状态
V1=L1S,T1=t1+273 K
末状态
V2=(L1+L2)S,T2=t2+273 K
据盖—吕萨克定律有
代入数据解得
T2=360K 或 t2=87 ℃
(2)初状态
V1=L1S,p1=p0+38 cmHg
末状态
V2=L 1S,p2=p0
据玻意尔定律有
p1V1=p2V2
解得
L 1=30cm
则从管口溢出的水银柱长度为
ΔL=6cm
21.(1)11cm;(2)100N
【详解】
(1)初态:,V0=h0S T0=t0+273=300K
末态:,V1=h1S T1=t1+273=330K
由盖吕萨克定律可得
解得
h1=11cm
(2)活塞距离汽缸底部的距离仍为10cm,由查理定律得
带入数据解得
对活塞
代入数据解得
F=100N
22.1.33×10-2m3
【详解】
一定质量的空气,在等压变化过程中,可以运用盖—吕萨克定律进行求解,空气的初、末状态参量分别为
初状态:T1=(273+27) K=300K,V1=1.0×10-2m3
末状态:T2=(273+127) K=400K
由盖—吕萨克定律得,气体温度升高127℃时的体积为
23.(1)12cm;(2)
【详解】
(1)密封气体初始体积
密封气体初始压强
左右两管均在同一水平面上时,体积
由玻意耳定律有
代入题给数据得
(2)密封气体再经等压膨胀过程体积变为
温度变为,由盖—吕萨克定律有
代入题给数据得
一、选择题(共15题)
1.夏天开空调,冷气从空调中吹进室内,则室内气体分子的
A.热运动剧烈程度加剧
B.平均动能变大
C.每个分子速率都会相应的减小
D.速率小的分子数所占的比例升高
2.一根两端封闭粗细均匀的直玻璃中有一段长57厘米的水银柱,在水银柱两边各有一段空气柱(如图).当玻璃管水平放置,两段空气柱长度均为30厘米,压强都是一个标准大气压,现将玻璃管缓慢竖立起来,则上下两段空气柱的长度分别为( )
A.30厘米,30厘米
B.35厘米,25厘米
C.40厘米,20厘米
D.45厘米,15厘米
3.压强的微观原因是气体分子对容器壁的作用,关于气体的压强,下列说法正确的是( )
A.气体压强的大小只与分子平均动能有关
B.单位体积内的分子数越多,分子平均速率越大,压强就越大
C.一定质量的气体,体积越小,温度越高,压强就越小
D.气体膨胀对外做功且温度降低,气体的压强可能不变
4.负压病房是收治传染性极强的呼吸道疾病病人所用的医疗设施,可以大大减少医务人员被感染的机会,病房中气压小于外界环境的大气压。若负压病房的温度和外界温度相同,负压病房内气体和外界环境中气体都可以看成理想气体,则以下说法正确的是( )
A.负压病房内气体分子的平均速率小于外界环境中气体分子的平均速率
B.负压病房内每个气体分子的运动速率都小于外界环境中每个气体分子的运动速率
C.负压病房内单位体积气体分子的个数小于外界环境中单位体积气体分子的个数
D.相同面积下,负压病房内壁受到的气体压力等于外壁受到的气体压力
5.一定质量的理想气体自状态A经状态B变化到状态C,这一过程在V-T图中表示如图所示,则下述结论错误的是 ( )
A.在过程AB中,气体压强不断变大 B.在过程BC中,气体密度不断变大
C.在过程AB中,气体对外界做功 D.在过程BC中,外界对气体做功
6.关于气体分子的运动情况,下列说法中正确的是( )
A.某一时刻具有某一速率的分子数目是相等的
B.某一时刻一个分子速度的大小和方向是偶然的
C.某一温度下,大多数气体分子的速率不会发生变化
D.分子的速率分布毫无规律
7.在“探究气体压强与体积的关系”的实验中。某同学在实验中测得的数据在计算机屏幕上显示如下表所示,仔细观察“p·V”一栏中的数值,发现越来越小,造成这一现象的原因可能是( )
序号 V(ml) p(×105Pa) p·V(×105Pa·ml)
1 20.0 1.0010 20.020
2 18.0 1.0952 19.714
3 16.0 1.2313 19.701
4 14.0 1.4030 19.642
5 12.0 1.6351 19.621
A.实验时注射器活塞与筒壁间的摩擦力越来越大
B.实验时环境温度升高了
C.实验时外界大气压强发生了变化
D.实验时注射器内的气体向外发生了泄漏
8.一定质量的某种理想气体,在不同温度下气体分子的运动速率分布曲线分别如图中实线和虚线所示,横坐标表示分子的运动速率,纵坐标表示单位速率间隔的分子数占总分子数的百分比,从图中可知( )
A.虚线对应的温度高 B.实线对应的分子平均动能大
C.相同体积下,虚线对应的气体压强大 D.相同压强下,实线对应的气体密度大
9.下列说法中正确的是
A.布朗运动反映了固体微粒中的分子运动的无规则性
B.对不同种类的物体,只要温度相同,分子的平均动能一定相同
C.分子间距离增大时,分子间的引力增大而斥力减小
D.一定质量的气体,温度升高时,分子间的平均距离一定增大
10.如图所示,一个横截面积为S的圆筒形容器竖直放置。金属圆板形活塞的下表面是水平的,上表面是倾斜的,上表面与水平面的夹角为θ,圆板的质量为M。不计圆板与容器内壁之间的摩擦。若大气压强为p0,则被圆板封闭在容器中的气体的压强p等于( )
A. B. C. D.
11.一定质量的理想气体,保持体积不变,压强减为原来的一半,则其温度由原来的27℃变为( )
A.127K B.150K C.13.5℃ D.-23.5℃
12.如图所示为某种一定质量的理想气体,由初态a经不同过程到达终态b,则关于a、b两点压强下列判断中正确的是( )
A. B. C. D.不能确定
13.活塞可以在气缸内自由移动,缸内贮有一定质量的理想气体,则气体可能发生的状态变化是( )
A.温度升高,压强减小,体积减小 B.温度降低,压强增大,体积减小
C.温度升高,压强减小,密度减小 D.温度降低,压强增大,密度不变
14.下面关于气体压强的说法正确的是( )
A.气体对器壁产生的压强是由于大量气体分子频繁碰撞器壁而产生的
B.气体对器壁产生的压强等于作用在器壁单位面积上的平均作用力
C.从微观角度看,气体压强的大小跟气体分子的平均动能和分子密集程度有关
D.从宏观角度看,气体压强的大小跟气体的温度和体积有关
15.如图所示,导热的汽缸固定在水平地面上,用活塞把一定质量的理想气体封闭在汽缸中,汽缸的内壁光滑.现用水平外力F作用于活塞杆,使活塞缓慢地向右移动,由状态①变化到状态②,在此过程中如果环境保持恒温,下列说法正确的是 ( )
A.每个气体分子的速率都不变
B.气体分子平均动能不变
C.水平外力F逐渐变大
D.气体内能减小
二、填空题
16.对于一定质量的理想气体,以p、V、T三个状态参量中的两个为坐标轴建立直角坐标系,在坐标系上描点能直观地表示这两个参量的数值.如图所示,两个坐标系中,两个点都表示相同质量某种理想气体的两个状态。根据坐标系中不同点的位置来比较第三个参量的大小。
(1)p T图象(图甲)中A、B两个状态,________状态体积小;
(2)V T图象(图乙)中C、D两个状态,________状态压强小。
17.如图所示,两端封闭的均匀半圆(圆心为O)管道内封闭一定质量理想气体,管内有不计质量、可自由移动的、绝热活塞P,将管内气体分成两部分。开始时OP与管道的水平直径的夹角为θ=45°,此时两部分气体压强均为P0=1.0×105Pa,温度相同。
(1)若缓慢升高左侧气体的温度,而保持右侧气体温度不变,当活塞缓慢移动到管道最低点(不计摩擦)时,右侧气体的压强为___________ Pa。
(2)若缓慢升高左侧气体的温度时,为保持活塞位置不变,则右侧气体的温度同时缓慢升高,应为左侧气体温度 ___________倍。
18.理想气体的状态方程表达式:______.
19.一定质量的理想气体,状态从A→B→C→D→A的变化过程可用如图所示的p-V图线描述,其中D→A为等温线,气体在状态A时温度为t=27 ℃,则气体在状态B时的温度为________K,气体从A到C过程对外做了_______J的功,气体在C状态时的温度为________℃。
三、综合题
20.如图所示,一端开口、内壁光滑的玻璃管竖直放置,管中用一段长 H0=38 cm 的水银柱封闭一段长 L1=20 cm 的空气,此时水银柱上端到管口的距离为 L2=4 cm,大气压强恒为 p0=76 cmHg,开始时封闭气体温度为 t1=27 ℃,取 0 ℃为 273 K.求:
(1)缓慢升高封闭气体温度至水银开始从管口溢出,此时封闭气体的温度;
(2)保持封闭气体初始温度 27 ℃不变,在竖直平面内从图示位置缓慢转动至玻璃管水平
过程中,求从管口溢出的水银柱的长度.(转动过程中没有发生漏气)
21.如图所示,一活塞将一定质量的理想气体封闭在固定导热汽缸内,活塞可沿汽缸无摩擦地滑动,活塞横截面积为,质量不计。开始时活塞距离汽缸底部为,外界大气压强,环境温度为℃。
(1)当环境温度缓慢升高至57℃时,活塞距离汽缸底部的距离为多少?
(2)当环境温度升高至57℃时,为使活塞距离汽缸底部的距离仍为,可对活塞施加一水平向左的推力F使活塞处于平衡状态,求推力F应为多大?
22.一定质量的空气,27℃时的体积为1.0×10-2m3,在压强不变的情况下,温度升高到127℃时体积是多大?
23.如图所示,粗细均匀、横截面积相等的U形管竖直放置,左管上端封闭,右管上端开口,两管高度均为。右管中有高的水银柱,水银柱上表面离管口的距离,管底水平段的体积可忽略。环境温度为。大气压强。现将型管水平放置,使左右两管均在同一水平面上。求∶
(1)此时水银柱与大气相通的表面到管口的距离;
(2)再将环境温度缓慢升高,使水银柱与大气相通的表面恰好与管口相平时的环境温度。
试卷第1页,共3页
参考答案:
1.D
【详解】
试题分析:冷气从空调中吹进室内,室内温度减小,分子热运动剧烈程度减小,分子平均动能减小,即速率小的分子数所占的比例升高,但不是每个分子的速率都减小,D正确.
2.C
【详解】
,
设左侧气体参数为
,
右侧气体为
,
根据理想气体状态方程
联立上述方程可以求得
3.B
【详解】
A.气体压强的大小与分子平均动能和分子的数密度有关,故A错误;
B.单位体积内的分子数越多,分子平均速率越大,压强就越大,故B正确;
C.一定质量的气体,体积越小,温度越高,压强就越大,故C错误;
D.根据理想气体状态方程可知,气体膨胀对外做功且温度降低,气体的压强一定变小,故D错误。
故选B。
4.C
【详解】
A.负压病房的温度和外界温度相同,故负压病房内气体分子的平均速率等于外界环境中气体分子的平均速率,故A错误;
B.负压病房内气体分子的平均运动速率相等,故不可能负压病房内每个气体分子的运动速率都小于外界环境中每个气体分子的运动速率,故B错误;
C.决定气体压强的微观因素:单位体积气体分子数和气体分子的平均速率,现内外温度相等,即气体分子平均速率相等,压强要减小形成负压,则要求负压病房内单位体积气体分子的个数小于外界环境中单位体积气体分子的个数,故C正确;
D.压力,内外压强不等,相同面积下,负压病房内壁受到的气体压力小于外壁受到的气体压力,故D错误。
故选C。
5.C
【详解】
C.在过程AB中,为等容变化,气体对外界做功为零,所以C项正确;
A.根据理想气体状态方程,温度升高过程中压强增大,所以A项错误;
D.在过程BC中,为等温变化,体积减小,外界对气体做功,D项错误;
B.一定质量的气体,体积减小,密度增大,B项错误。
故选C。
6.B
【详解】
AD.具有某一速率的分子数目并不是相等的,呈“中间多,两头少”的统计规律分布,故AD错误;
B.由于分子之间不断地碰撞,分子随时都会改变自己的运动情况,因此在某一时刻,一个分子速度的大小和方向完全是偶然的,故B正确;
C.某一温度下,每个分子的速率仍然是随时变化的,只是分子运动的平均速率不变,故C错误。
故选B。
7.D
【详解】
A.实验时注射器活塞与筒壁间的摩擦力不断增大,不会影响气压与体积,故A错误;
B.实验时环境温度增大了,根据理想气体状态方程
PV乘积变大,故B错误;
C.封闭气体压强与外界大气压强无关,故C错误;
D.实验时注射器的空气向外发生了泄漏,根据理想气体状态方程
常数C与质量有关,变小,故PV乘积减小,故D正确;
故选D。
8.B
【详解】
AB.由图可知图中实线对应的速率较大,由于温度越高,速率大的分子占的比例越大,则实线对应的气体分子温度较高,温度是平均动能的标志,图中实线对应的温度高,则分子平均动能大,故B正确,A错误;
C.由理想气体状态方程
可得相同体积下,实线对应的气体压强大,故C错误;
D.由
联立可得
可得质量相同,压强相同,温度越高,密度越小,故D错误。
故选B。
9.B
【详解】
A:布朗运动反映了液体中分子运动的无规则性.故A项错误.
B:温度是分子平均动能的标志,对不同种类的物体,只要温度相同,分子的平均动能一定相同.故B项正确.
C:分子间距离增大时,分子间的引力、斥力均减小.故C项错误.
D:一定质量的气体,温度升高时,压强如果同时也有变化,则气体体积的变化不能确定,因而气体分子间的平均距离不一定增大.故D项错误.
10.D
【详解】
以活塞为研究对象,分析受力有:重力Mg、外界大气压力p0S,气缸壁的压力N和缸内气体的压力F,受力分析图如下
其中
F = p
根据平衡条件得
p0S + mg = Fcosθ
联立求解得
p = p0 +
故选D。
11.B
【详解】
根据气体做等容变化有
则压强减为原来的一半时,热力学温度也减为原来的一半,则有
所以B正确;ACD错误;
故选B。
12.C
【详解】
根据理想气体状态方程有
由此可得图像的斜率,即斜率越大,压强越小,如图所示
所以有,故选C。
13.BC
【详解】
AC.根据
可知,温度升高,压强减小,体积必然要增大,密度减小,选项A错误,C正确;
BD.根据
可知,温度降低,压强增大,体积减小,密度增大,选项B正确,D错误;
故选BC。
14.ABCD
【详解】
A.气体对器壁产生的压强是由于大量气体分子频繁碰撞器壁而产生的,选项A正确;
B.气体对器壁产生的压强等于作用在器壁上单位面积的平均作用力,选项B正确;
C.从微观角度看,气体压强的大小跟气体分子的平均动能和分子密集程度有关,分子平均动能越大,则分子撞击器壁的作用力越大,压强越大;分子密度越大,则单位时间撞击器壁单位面积上的分子数越多,则压强越大,选项C正确;
D.从宏观的角度看,温度越高,分子的平均速率越大,分子的平均动能越大,体积越小,单位时间内的气体分子数越多,分子对器壁的碰撞越频繁,气体对器壁的压强就越大,否则压强就越小,选项D正确。
故选ABCD。
15.BC
【详解】
试题分析:封闭气体等温膨胀过程,温度是分子热运动平均动能的标志,故分子热运动的平均动能不变,不是每个分子动能都不变,所以A错误;气体等温膨胀,温度不变,则气体分子的平均动能不变,B正确;温度不变,体积增大,根据,则压强P减小,以活塞为研究对象,根据平衡条件:,得:,压强P减小,则F增大,C正确;理想气体的内能只与温度有关,温度不变,则内能不变,故D错误.
16. A C
【详解】
甲图画出的倾斜直线为等容线,斜率越小,体积越大,所以VB>VA。
乙图画出的倾斜直线为等压线,斜率越小,压强越大,所以pD>pC。
17. 1.5×105 1
【详解】
(1)对于管道右侧气体,由于气体做等温变化,则有:
p0V1=p2V2
解得
p2=1.5×105Pa
(2)左右两边气体的体积均不变,则对左侧气体
对右侧气体
p左=p右
则
T左=T右
即右侧气体的温度应为左侧气体温度1倍。
18. =C.
19. 750 6×105 102
【详解】
A到B过程气体做等压变化,则
TA=27 ℃+273 K=300 K
解得
TB=750 K
从A到B过程气体对外界做功
W=pΔV=6×105 J
从B到C过程体积不变,所以外界对气体不做功,所以气体从A到C过程气体对外界做功为6×105 J;
气体在C状态压强为B时的一半,则温度也为B时的一半,即
tC=375 K=102 ℃
20.(1)87 ℃;(2)6cm
【详解】
试题分析:(1)设玻璃管横截面积为 S,初状态
V1=L1S,T1=t1+273 K
末状态
V2=(L1+L2)S,T2=t2+273 K
据盖—吕萨克定律有
代入数据解得
T2=360K 或 t2=87 ℃
(2)初状态
V1=L1S,p1=p0+38 cmHg
末状态
V2=L 1S,p2=p0
据玻意尔定律有
p1V1=p2V2
解得
L 1=30cm
则从管口溢出的水银柱长度为
ΔL=6cm
21.(1)11cm;(2)100N
【详解】
(1)初态:,V0=h0S T0=t0+273=300K
末态:,V1=h1S T1=t1+273=330K
由盖吕萨克定律可得
解得
h1=11cm
(2)活塞距离汽缸底部的距离仍为10cm,由查理定律得
带入数据解得
对活塞
代入数据解得
F=100N
22.1.33×10-2m3
【详解】
一定质量的空气,在等压变化过程中,可以运用盖—吕萨克定律进行求解,空气的初、末状态参量分别为
初状态:T1=(273+27) K=300K,V1=1.0×10-2m3
末状态:T2=(273+127) K=400K
由盖—吕萨克定律得,气体温度升高127℃时的体积为
23.(1)12cm;(2)
【详解】
(1)密封气体初始体积
密封气体初始压强
左右两管均在同一水平面上时,体积
由玻意耳定律有
代入题给数据得
(2)密封气体再经等压膨胀过程体积变为
温度变为,由盖—吕萨克定律有
代入题给数据得
同课章节目录
- 第1章 分子动理论
- 1.1 走进分子世界
- 1.2 无序中的有序
- 1.3 分子动理论 内能
- 第2章 气体定律与人类生活
- 2.1 气体的状态
- 2.2 玻意耳定律
- 2.3 查理定律和盖-吕萨克定律
- 第3章 固体、液体与新材料
- 3.1 固体的性质
- 3.2 液体的表面性质
- 3.3 液晶与显示器
- 3.4 半导体材料和纳米材料
- 第4章 热力学定律
- 4.1 热力学第一定律
- 4.2 能量守恒定律
- 4.3 热力学第二定律
- 第5章 原子世界探秘
- 5.1 电子的发现
- 5.2 原子模型的提出
- 5.3 量子论视野下的原子模型
- 第6章 波粒二象性
- 6.1 光电效应现象
- 6.2 光电效应的理论解释
- 6.3 光的波粒二象性
- 6.4 实物粒子具有波动性
- 第7章 原子核与核能
- 7.1 原子核结构探秘
- 7.2 原子核的衰变
- 7.3 原子核的结合能
- 7.4 裂变与聚变
- 7.5 粒子物理与宇宙起源
