第五章一次函数的导数及其应用 达标测试卷-2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册(含答案)
文档属性
| 名称 | 第五章一次函数的导数及其应用 达标测试卷-2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册(含答案) | 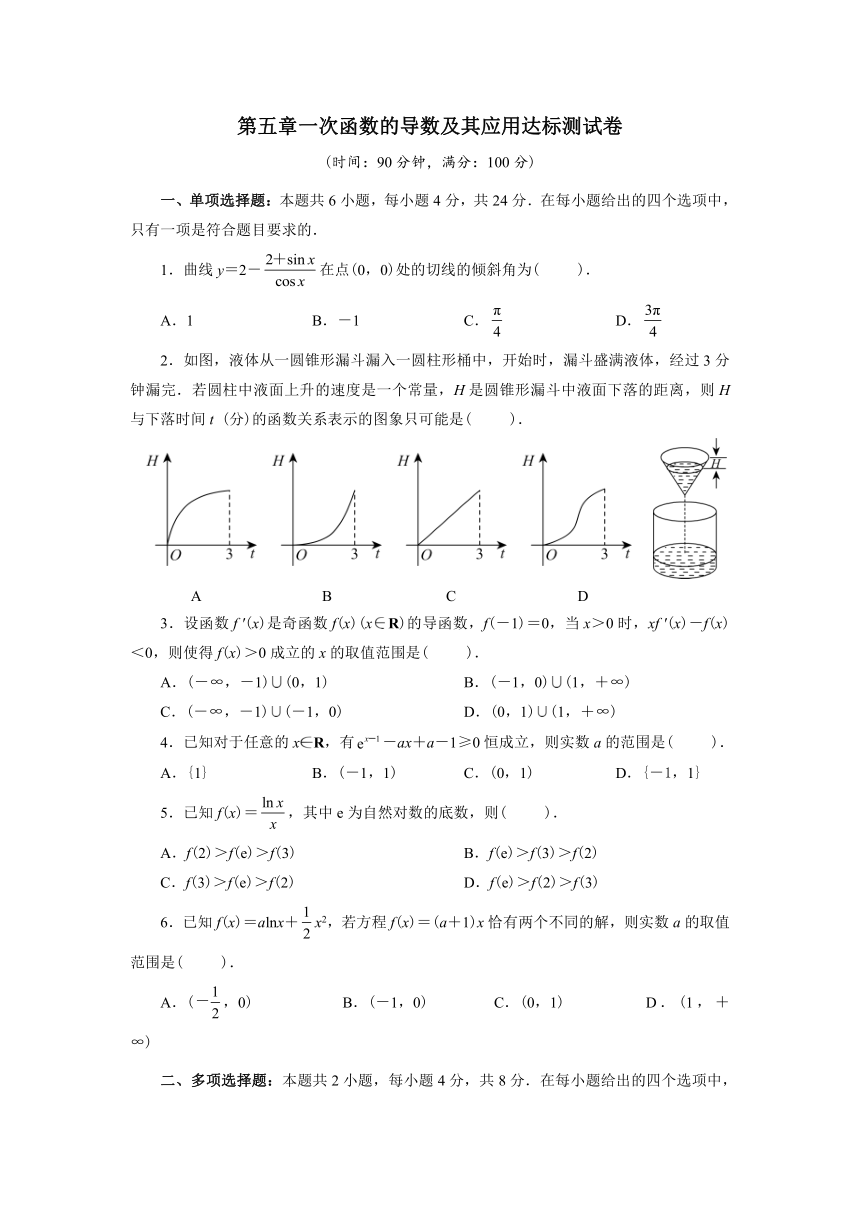 | |
| 格式 | docx | ||
| 文件大小 | 216.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 20:20:08 | ||
图片预览




文档简介
第五章一次函数的导数及其应用达标测试卷
(时间:90分钟,满分:100分)
一、单项选择题:本题共6小题,每小题4分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.曲线y=2-在点(0,0)处的切线的倾斜角为( ).
A.1 B.-1 C. D.
2.如图,液体从一圆锥形漏斗漏入一圆柱形桶中,开始时,漏斗盛满液体,经过3分钟漏完.若圆柱中液面上升的速度是一个常量,H是圆锥形漏斗中液面下落的距离,则H与下落时间t (分)的函数关系表示的图象只可能是( ).
A B C D
3.设函数f '(x)是奇函数f(x)(xR)的导函数,f(-1)=0,当x>0时,xf '(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是( ).
A.(-∞,-1)(0,1) B.(-1,0)(1,+∞)
C.(-∞,-1)(-1,0) D.(0,1)(1,+∞)
4.已知对于任意的xR,有-ax+a-1≥0恒成立,则实数a的范围是( ).
A.{1} B.(-1,1) C.(0,1) D.{-1,1}
5.已知f(x)=,其中e为自然对数的底数,则( ).
A.f(2)>f(e)>f(3) B.f(e)>f(3)>f(2)
C.f(3)>f(e)>f(2) D.f(e)>f(2)>f(3)
6.已知f(x)=alnx+x2,若方程f(x)=(a+1)x恰有两个不同的解,则实数a的取值范围是( ).
A.(,0) B.(-1,0) C.(0,1) D.(1,+∞)
二、多项选择题:本题共2小题,每小题4分,共8分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得4分,部分选对的得2分,有选错的得0分.
7.已知函数f(x)=ex·x3,则以下结论正确的是( ).
A.f(x)在R上单调递增
B.f(log5 2)<<f(ln π)
C.方程f(x)=-1有实数解
D.存在实数,使得方程f(x)=x有4个实数解
8.设f(x)=xa·cos x,x的最大值为M,则( ).
A.当a=-1时,M< B.当a=1时,M>
C.当a=2时,M< D.当a=3时,M<
三、填空题:本题共5小题,每小题4分,共20分.将答案填在题后的横线上.
9.设f(x)=cos(2x+φ),若y=2f(x)+f '(x)为奇函数,则常数φ的一个取值为_______
_____.
10.函数f(x)=cos3x+sin2x-cosx的最大值等于__________.
11.一艘轮船在航行中的燃料费和它的速度的立方成正比,且轮船的最大速度为每小时m海里.已知速度为每小时10海里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元.要使轮船每海里的总费用最少,则轮船的速度为__________.
12.已知函数f(x)=-x3+9x2-26x+27,f(x)在x=x1,x2(x1≠x2)处导数相等,则x1+x2=__________.
13.已知函数f(x)=x3-ax,对于任意的x[-1,1],有|f(x)|≤恒成立,则a的取值范围是__________.
四、解答题:本题共5小题,共48分.解答应写出文字说明、证明过程或演算步骤.
14.(8分)已知函数f(x)=aex-2x2.
(1)当a=1时,求函数f(x)在x=2处的切线方程;
(2)若不等式f '(x)≥0在R上恒成立,试求a的取值范围.
15.(10分)已知函数f(x)=x3+2bx2+cx-2的图象在与x轴交点处的切线方程是y=5x-10.
(1)求函数f(x)的解析式;
(2)设函数g(x)=f(x)+mx,若g(x)的极值存在,求实数m的取值范围,并求函数g(x)的极值点.
16.(10分)已知f(x)=x2+lnx.
(1)求函数f(x)的单调区间;
(2)当x[t,t+1]时(t为大于0的常数),求f(x)的最大值;
(3)若当≤x2<x1≤1时,不等式f(x1)-f(x2)<(x1-x2)恒成立,求的取值范围.
17.(10分)设函数f(x)=ex-ax+3(aR).
(1)讨论函数f(x)的单调性;
(2)若函数f(x)在区间[1,2]上的最小值是4,求a的值.
18.(10分)数据显示,公园中每天空气质量指数近似满足函数f(x)=mlnx-x+-6(4≤x≤22,mR),其中x为每天的时刻.若凌晨6时,测得空气质量指数为29.6.
(1)求实数m的值;
(2)求近期每天空气质量指数最高的时刻.(参考数值:ln6=1.8)
参考答案
一、单项选择题.
1.D.
2.B.
3.A.
提示:由导数的运算法则可得,因此当x(0,+∞)时,<0,单调递减.又f(-1)=0,f(x)(xR)是奇函数,所以当x(-∞,-1)或x(0,1)时,f(x)>0.
4.A.
5.B.
6.A.
二、多项选择题.
7.BCD.
提示:f(x)=ex·x3,则f '(x)=ex·x3+ex·3x2=x2ex(x+3),
故函数在(-∞,-3)上单调递减,在(-3,+∞)上单调递增,A错误;
0<log52<,<<1,ln π>1,根据单调性知f(log52)<<f(ln π),B正确;
f(0)=0,f(-3)=-<-1,故方程f(x)=-1有实数解,C正确;
f(x)=x,易知当x=0时成立,当x≠0时,==exx2,设g(x)=exx2,
则g '(x)=exx(x+2),故函数在(0,+∞)上单调递增,在(-2,-0)内单调递减,在(-∞,-2)上单调递增,且g(-2)=.
画出函数图象如图所示,当0<<时有3个交点.
综上所述:存在实数,使得方程f(x)=x有4个实数解,D正确.故选BCD.
8.AC.
提示:对于选项A,当a=-1时,f(x)=在区间上单调递减,
所以M=,故A正确.
对于选项B,当a=1时,当x时,恒成立,
所以当x时,f(x)=xcos x<tan x cos x=sin x≤,所以M<,故B错误.
对于选项C,当a=2时,f(x)=x2·cos x,则f '(x)=xcos x(2-xtan x)>0,
所以f(x)在区间上单调递增,即M=,故C正确.
对于选项D,当a=3时,f(x)=x3·cos x,则f '(x)=x2 cos x(3-xtan x)>0,
所以f(x)在区间上单调递增,所以M=·>,故D错误.故选AC.
三、填空题.
9.(答案不唯一,满足φ=π+(Z)的任意一个值均可).
10..
11.v=
12.6.
13..
四、解答题.
14.解:(1)因为f(x)=aex-2x2,所以f '(x)=aex-4x.
当a=1时,f(2)=e2-8,f '(2)=e2-8,所以f(x)在x=2处的切线方程为y-(e2-8)=(e2-8)(x-2),即y=(e2-8)(x-1).
(2)根据题意,若函数f(x)为R上的单调递增函数,则f '(x)=aex-4x≥0恒成立,即a≥恒成立,则有a≥g(x)max.
令g(x)=,则g'(x)=.
当x>1时,g'(x)<0;当x<1时,g'(x)>0,所以g(x)max=g(1)=.
所以a的取值范围是a≥.
15.解:(1)由已知,切点为(2,0),故有f(2)=0,即4b+c+3=0. ①
又f '(x)=3x2+4bx+c,由已知f '(2)=12+8b+c=5得8b+c+7=0. ②
联立①②,解得b=-1,c=1.所以函数的解析式为f(x)=x3-2x2+x-2.
(2)因为g(x)=x3-2x2+x-2+mx,则g'(x)=3x2-4x+1+m=0.
当函数有极值时,则≥0,方程3x2-4x+1+m=0有实数解.
由=4(1-m)≥0,得m≤1.
当m=1时,g'(x)=0有实数x=,在x=左右两侧均有g'(x)>0,
此时函数g(x)无极值;
当m<1时,g'(x)=0有两个实数根x1=,x2=,列表讨论如下:
x (-∞,x1) x1 (x1,x2) x2 (x2,+∞)
g'(x) + 0 - 0 +
g(x) 极大值 极小值
所以在m(-∞,1)时,函数g(x)有极值,且g(x)的极大值点是x=;极小值点是x=.
16.解:(1)由f(x)=x2+lnx,可知x(0,+∞),f '(x)=-x+=.
由f '(x)=>0,x>0,得0<x<1;由f '(x)=<0,x>0,得x>1.
所以函数f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞).
(2)①当0<t≤1时,1[t,t+1],所以f(x)max=f(1)=.
②当t>1时,f(x)在[t,t+1]为减函数,所以f(x)max=f(t)=t2+lnt.
(3)当≤x2<x1≤1时,不等式f(x1)-f(x2)<(x1-x2),即f(x1)-x1<f(x2)-x2恒成立.令g(x)=f(x)-x,则g(x1)<g(x2),则g(x)在[,1]为是减函数,所以g '(x)=f '(x)-=-x+-≤0,即≥-x恒成立.
所以≥(-x)max=.
17.解:(1)f '(x)=ex-a,当a≤0时,f '(x)>0,f(x)在R上单调递增;
当a>0时,f '(x)>0解得x>lna,由f '(x)<0解得x<lna.
综上所述:当a≤0时,函数f(x)在R上单调递增;
当a>0时,函数f(x)在(lna,+∞)上单调递增,在(-∞,lna)上单调递减.
(2)由(1)知,当a≤0时,函数f(x)在R上单调递增,
所以函数f(x)在[1,2]上的最小值为f(1)=e-a+3=4,即a=e-1>0,矛盾.
当a>0时,x=lna是函数f(x)在R上的极小值点.
①当lna≤1即0<a<e时,函数f(x)在[1,2]上单调递增,
则函数f(x)的最小值为f(1)=e-a+3=4,即a=e-1>0,符合条件.
②当lna≥2即a≥e2时,函数f(x)在[1,2]上单调递减,
则函数f(x)的最小值为f(2)=e2-2a+3=4即a=<e2,矛盾.
③当1<lna<2即e<lna<e2时,函数f(x)在[1,lna]上单调递减,函数f(x)在[lna,2]上单调递增,则函数f(x)的最小值为f(lna)=elna-alna+3=4,即a-alna-1=0.
令h(a)=a-alna-1(e<a<e2),则h'(a)=-lna<0,
所以h(a)在(e,e2)上单调递减,而h(e)=-1,所以h(a)在(e,e2)上没有零点,
即当e<a<e2时,a-alna-1=0无解.
综上,实数a的值为e-1.
18.解:(1)由f(6)=29.6,代入f(x)=mlnx-x+-6,解得m=,12.
(2)由已知函数求导,得f '(x)=,令f '(x)=0,得x=12.
列表,得
x [4,12) 12 (12,22]
f '(x) + 0 -
f(x) 单调递增 极大值 单调递减
所以函数在x=12时,取极大值,也是最大值,
即每天时段空气质量指数最高时刻为12时.
答:(1)实数m的值为12;(2)空气质量指数最高的时刻为12时.
(时间:90分钟,满分:100分)
一、单项选择题:本题共6小题,每小题4分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.曲线y=2-在点(0,0)处的切线的倾斜角为( ).
A.1 B.-1 C. D.
2.如图,液体从一圆锥形漏斗漏入一圆柱形桶中,开始时,漏斗盛满液体,经过3分钟漏完.若圆柱中液面上升的速度是一个常量,H是圆锥形漏斗中液面下落的距离,则H与下落时间t (分)的函数关系表示的图象只可能是( ).
A B C D
3.设函数f '(x)是奇函数f(x)(xR)的导函数,f(-1)=0,当x>0时,xf '(x)-f(x)<0,则使得f(x)>0成立的x的取值范围是( ).
A.(-∞,-1)(0,1) B.(-1,0)(1,+∞)
C.(-∞,-1)(-1,0) D.(0,1)(1,+∞)
4.已知对于任意的xR,有-ax+a-1≥0恒成立,则实数a的范围是( ).
A.{1} B.(-1,1) C.(0,1) D.{-1,1}
5.已知f(x)=,其中e为自然对数的底数,则( ).
A.f(2)>f(e)>f(3) B.f(e)>f(3)>f(2)
C.f(3)>f(e)>f(2) D.f(e)>f(2)>f(3)
6.已知f(x)=alnx+x2,若方程f(x)=(a+1)x恰有两个不同的解,则实数a的取值范围是( ).
A.(,0) B.(-1,0) C.(0,1) D.(1,+∞)
二、多项选择题:本题共2小题,每小题4分,共8分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得4分,部分选对的得2分,有选错的得0分.
7.已知函数f(x)=ex·x3,则以下结论正确的是( ).
A.f(x)在R上单调递增
B.f(log5 2)<<f(ln π)
C.方程f(x)=-1有实数解
D.存在实数,使得方程f(x)=x有4个实数解
8.设f(x)=xa·cos x,x的最大值为M,则( ).
A.当a=-1时,M< B.当a=1时,M>
C.当a=2时,M< D.当a=3时,M<
三、填空题:本题共5小题,每小题4分,共20分.将答案填在题后的横线上.
9.设f(x)=cos(2x+φ),若y=2f(x)+f '(x)为奇函数,则常数φ的一个取值为_______
_____.
10.函数f(x)=cos3x+sin2x-cosx的最大值等于__________.
11.一艘轮船在航行中的燃料费和它的速度的立方成正比,且轮船的最大速度为每小时m海里.已知速度为每小时10海里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元.要使轮船每海里的总费用最少,则轮船的速度为__________.
12.已知函数f(x)=-x3+9x2-26x+27,f(x)在x=x1,x2(x1≠x2)处导数相等,则x1+x2=__________.
13.已知函数f(x)=x3-ax,对于任意的x[-1,1],有|f(x)|≤恒成立,则a的取值范围是__________.
四、解答题:本题共5小题,共48分.解答应写出文字说明、证明过程或演算步骤.
14.(8分)已知函数f(x)=aex-2x2.
(1)当a=1时,求函数f(x)在x=2处的切线方程;
(2)若不等式f '(x)≥0在R上恒成立,试求a的取值范围.
15.(10分)已知函数f(x)=x3+2bx2+cx-2的图象在与x轴交点处的切线方程是y=5x-10.
(1)求函数f(x)的解析式;
(2)设函数g(x)=f(x)+mx,若g(x)的极值存在,求实数m的取值范围,并求函数g(x)的极值点.
16.(10分)已知f(x)=x2+lnx.
(1)求函数f(x)的单调区间;
(2)当x[t,t+1]时(t为大于0的常数),求f(x)的最大值;
(3)若当≤x2<x1≤1时,不等式f(x1)-f(x2)<(x1-x2)恒成立,求的取值范围.
17.(10分)设函数f(x)=ex-ax+3(aR).
(1)讨论函数f(x)的单调性;
(2)若函数f(x)在区间[1,2]上的最小值是4,求a的值.
18.(10分)数据显示,公园中每天空气质量指数近似满足函数f(x)=mlnx-x+-6(4≤x≤22,mR),其中x为每天的时刻.若凌晨6时,测得空气质量指数为29.6.
(1)求实数m的值;
(2)求近期每天空气质量指数最高的时刻.(参考数值:ln6=1.8)
参考答案
一、单项选择题.
1.D.
2.B.
3.A.
提示:由导数的运算法则可得,因此当x(0,+∞)时,<0,单调递减.又f(-1)=0,f(x)(xR)是奇函数,所以当x(-∞,-1)或x(0,1)时,f(x)>0.
4.A.
5.B.
6.A.
二、多项选择题.
7.BCD.
提示:f(x)=ex·x3,则f '(x)=ex·x3+ex·3x2=x2ex(x+3),
故函数在(-∞,-3)上单调递减,在(-3,+∞)上单调递增,A错误;
0<log52<,<<1,ln π>1,根据单调性知f(log52)<<f(ln π),B正确;
f(0)=0,f(-3)=-<-1,故方程f(x)=-1有实数解,C正确;
f(x)=x,易知当x=0时成立,当x≠0时,==exx2,设g(x)=exx2,
则g '(x)=exx(x+2),故函数在(0,+∞)上单调递增,在(-2,-0)内单调递减,在(-∞,-2)上单调递增,且g(-2)=.
画出函数图象如图所示,当0<<时有3个交点.
综上所述:存在实数,使得方程f(x)=x有4个实数解,D正确.故选BCD.
8.AC.
提示:对于选项A,当a=-1时,f(x)=在区间上单调递减,
所以M=,故A正确.
对于选项B,当a=1时,当x时,恒成立,
所以当x时,f(x)=xcos x<tan x cos x=sin x≤,所以M<,故B错误.
对于选项C,当a=2时,f(x)=x2·cos x,则f '(x)=xcos x(2-xtan x)>0,
所以f(x)在区间上单调递增,即M=,故C正确.
对于选项D,当a=3时,f(x)=x3·cos x,则f '(x)=x2 cos x(3-xtan x)>0,
所以f(x)在区间上单调递增,所以M=·>,故D错误.故选AC.
三、填空题.
9.(答案不唯一,满足φ=π+(Z)的任意一个值均可).
10..
11.v=
12.6.
13..
四、解答题.
14.解:(1)因为f(x)=aex-2x2,所以f '(x)=aex-4x.
当a=1时,f(2)=e2-8,f '(2)=e2-8,所以f(x)在x=2处的切线方程为y-(e2-8)=(e2-8)(x-2),即y=(e2-8)(x-1).
(2)根据题意,若函数f(x)为R上的单调递增函数,则f '(x)=aex-4x≥0恒成立,即a≥恒成立,则有a≥g(x)max.
令g(x)=,则g'(x)=.
当x>1时,g'(x)<0;当x<1时,g'(x)>0,所以g(x)max=g(1)=.
所以a的取值范围是a≥.
15.解:(1)由已知,切点为(2,0),故有f(2)=0,即4b+c+3=0. ①
又f '(x)=3x2+4bx+c,由已知f '(2)=12+8b+c=5得8b+c+7=0. ②
联立①②,解得b=-1,c=1.所以函数的解析式为f(x)=x3-2x2+x-2.
(2)因为g(x)=x3-2x2+x-2+mx,则g'(x)=3x2-4x+1+m=0.
当函数有极值时,则≥0,方程3x2-4x+1+m=0有实数解.
由=4(1-m)≥0,得m≤1.
当m=1时,g'(x)=0有实数x=,在x=左右两侧均有g'(x)>0,
此时函数g(x)无极值;
当m<1时,g'(x)=0有两个实数根x1=,x2=,列表讨论如下:
x (-∞,x1) x1 (x1,x2) x2 (x2,+∞)
g'(x) + 0 - 0 +
g(x) 极大值 极小值
所以在m(-∞,1)时,函数g(x)有极值,且g(x)的极大值点是x=;极小值点是x=.
16.解:(1)由f(x)=x2+lnx,可知x(0,+∞),f '(x)=-x+=.
由f '(x)=>0,x>0,得0<x<1;由f '(x)=<0,x>0,得x>1.
所以函数f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞).
(2)①当0<t≤1时,1[t,t+1],所以f(x)max=f(1)=.
②当t>1时,f(x)在[t,t+1]为减函数,所以f(x)max=f(t)=t2+lnt.
(3)当≤x2<x1≤1时,不等式f(x1)-f(x2)<(x1-x2),即f(x1)-x1<f(x2)-x2恒成立.令g(x)=f(x)-x,则g(x1)<g(x2),则g(x)在[,1]为是减函数,所以g '(x)=f '(x)-=-x+-≤0,即≥-x恒成立.
所以≥(-x)max=.
17.解:(1)f '(x)=ex-a,当a≤0时,f '(x)>0,f(x)在R上单调递增;
当a>0时,f '(x)>0解得x>lna,由f '(x)<0解得x<lna.
综上所述:当a≤0时,函数f(x)在R上单调递增;
当a>0时,函数f(x)在(lna,+∞)上单调递增,在(-∞,lna)上单调递减.
(2)由(1)知,当a≤0时,函数f(x)在R上单调递增,
所以函数f(x)在[1,2]上的最小值为f(1)=e-a+3=4,即a=e-1>0,矛盾.
当a>0时,x=lna是函数f(x)在R上的极小值点.
①当lna≤1即0<a<e时,函数f(x)在[1,2]上单调递增,
则函数f(x)的最小值为f(1)=e-a+3=4,即a=e-1>0,符合条件.
②当lna≥2即a≥e2时,函数f(x)在[1,2]上单调递减,
则函数f(x)的最小值为f(2)=e2-2a+3=4即a=<e2,矛盾.
③当1<lna<2即e<lna<e2时,函数f(x)在[1,lna]上单调递减,函数f(x)在[lna,2]上单调递增,则函数f(x)的最小值为f(lna)=elna-alna+3=4,即a-alna-1=0.
令h(a)=a-alna-1(e<a<e2),则h'(a)=-lna<0,
所以h(a)在(e,e2)上单调递减,而h(e)=-1,所以h(a)在(e,e2)上没有零点,
即当e<a<e2时,a-alna-1=0无解.
综上,实数a的值为e-1.
18.解:(1)由f(6)=29.6,代入f(x)=mlnx-x+-6,解得m=,12.
(2)由已知函数求导,得f '(x)=,令f '(x)=0,得x=12.
列表,得
x [4,12) 12 (12,22]
f '(x) + 0 -
f(x) 单调递增 极大值 单调递减
所以函数在x=12时,取极大值,也是最大值,
即每天时段空气质量指数最高时刻为12时.
答:(1)实数m的值为12;(2)空气质量指数最高的时刻为12时.
