2021-2022学年 北师大版七年级数学下册 1.4 整式的乘法 同步练习题(Word版 含答案)
文档属性
| 名称 | 2021-2022学年 北师大版七年级数学下册 1.4 整式的乘法 同步练习题(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 95.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 22:21:55 | ||
图片预览


文档简介
2021-2022学年北师大版七年级数学下册《1-4整式的乘法》同步练习题(附答案)
1.计算8a3x3 (﹣2ax)3的结果是( )
A.0 B.﹣64a6x6 C.﹣16a6x6 D.﹣48x4a6
2.小明在做作业的时候,不小心把墨水滴到了作业本上,▄×2ab=4a2b+2ab3,阴影部分即为被墨汁弄污的部分,那么被墨汁遮住的一项是( )
A.(2a+b2) B.(a+2b) C.(3ab+2b2) D.(2ab+b2)
3.计算(﹣2x+1)(﹣3x2)的结果为( )
A.6x3+1 B.6x3﹣3 C.6x3﹣3x2 D.6x3+3x2
4.如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( )
A.﹣3 B.3 C.0 D.1
5.通过计算几何图形的面积可表示一些代数恒等式,右图可表示的代数恒等式是( )
A.(a﹣b)2=a2﹣2ab+b2 B.2a(a+b)=2a2+2ab
C.(a+b)2=a2+2ab+b2 D.(a+b)(a﹣b)=a2﹣b2
6.一个长方体的长、宽、高分别是3m﹣4,2m和m,则它的体积是( )
A.3m3﹣4m2 B.3m2﹣4m3 C.6m3﹣8m2 D.6m2﹣8m3
7.如图,正方形卡片A类,B类和长方形卡片C类若干张,如果要拼一个长为(a+2b),宽为(3a+b)的大长方形,则需要C类卡片( )张.
A.5 B.6 C.7 D.8
8.如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式,你认为其中正确的有( )
①(2a+b)(m+n); ②2a(m+n)+b(m+n);
③m(2a+b)+n(2a+b);④2am+2an+bm+bn.
A.①② B.③④ C.①②③ D.①②③④
9.若(x+m)(x﹣8)=x2+2x+n,则代数式m﹣n的值为( )
A.90 B.﹣70 C.﹣90 D.58
10.已知m+n=2,mn=﹣2,则(1﹣m)(1﹣n)的值为( )
A.﹣1 B.1 C.﹣3 D.5
11.计算:(3x2)2 2x3= .
12.光的速度每秒约3×105千米,太阳光射到地球上需要的时间约是5×102秒,则地球与太阳的距离约是 千米.
13.若x+y=3且xy=1,则代数式(1+x)(1+y)= .
14.化简:(2x﹣y)(x+3y)= .
15.关于x的代数式(3﹣ax)(x2+2x﹣1)的展开式中不含x2项,则a= .
16.对于实数a,b,c,d,规定一种运算=ad﹣bc,如=1×(﹣2)﹣0×2=﹣2,那么当=27时,则x= .
17.计算:(﹣2a2)2﹣3a4+2a (﹣3a3)
18.计算:(x+2)(x﹣7)﹣3x.
19.先阅读材料,再解答问题:
例:已知x=123456789×123456786,y=123456788×123456787,试比较x、y的大小.
解:设123456788=a,则x=(a+1)(a﹣2)=a2﹣a﹣2,y=a(a﹣1)=a2﹣a,
∵x﹣y=(a2﹣a﹣2)﹣(a2﹣a)=﹣2,∴x<y.
问题:已知x=20222022×20222026﹣20222023×20222025,
y=20222023×20222027﹣20222024×20222026,试比较x、y的大小.
20.某市有一块长为3a+b米,宽为2a+b米的长方形地块,规划部门计划将阴影部分进行绿化中间修建一座边长是(a﹣b)的正方形雕像.
(1)请用含a,b的代数式表示绿化面积s;
(2)当a=3,b=2时,求绿化面积.
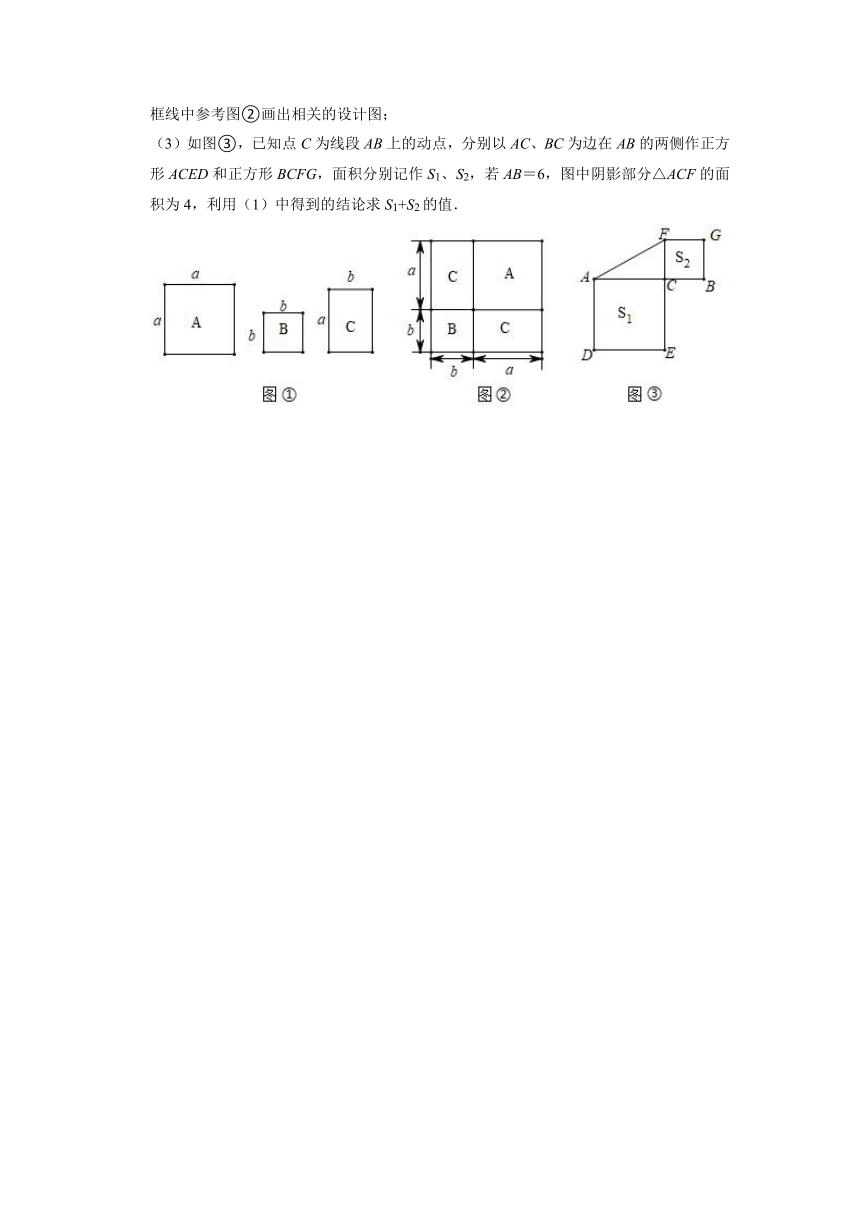
21.数学活动课上,老师用图①中的1张边长为a的正方形A、1张边长为b的正方形B和2张宽和长分别为a与b的长方形C纸片,排成了如图②中的大正方形.观察图形并解答下列问题.
(1)由图①和图②可以得到的等式为 (用含a,b的代数式表示);
(2)小芳想用图①的三种纸片拼出一个面积为(a+b)(a+2b)的大长方形,则需要A纸片 张,B纸片 张,C纸片 张(空格处填写数字),并尝试在框线中参考图②画出相关的设计图;
(3)如图③,已知点C为线段AB上的动点,分别以AC、BC为边在AB的两侧作正方形ACED和正方形BCFG,面积分别记作S1、S2,若AB=6,图中阴影部分△ACF的面积为4,利用(1)中得到的结论求S1+S2的值.
参考答案
1.解:8a3x3 (﹣2ax)3=8a3x3 (﹣8a3x3)=﹣64a6x6.
故选:B.
2.解:被墨汁遮住部分=(4a2b+2ab3)÷2ab=4a2b÷2ab+2ab3÷2ab=2a+b2,
故选:A.
3.解:原式=6x3﹣3x2.
故选:C.
4.解:∵(x+m)(x+3)=x2+3x+mx+3m=x2+(3+m)x+3m,
又∵(x+m)与(x+3)的乘积中不含x的一次项,
∴3+m=0,
解得m=﹣3.
故选:A.
5.解:长方形的面积等于:2a(a+b),
也等于四个小图形的面积之和:a2+a2+ab+ab=2a2+2ab,
即2a(a+b)=2a2+2ab.
故选:B.
6.解:根据长方体体积的计算公式得,(3m﹣4) 2m m=6m3﹣8m2,
故选:C.
7.解:∵(a+2b)(3a+b)
=3a2+7ab+2b2
∵一张C类卡片的面积为ab
∴需要C类卡片7张.
故选:C.
8.解:表示该长方形面积的多项式
①(2a+b)(m+n)正确;
②2a(m+n)+b(m+n)正确;
③m(2a+b)+n(2a+b)正确;
④2am+2an+bm+bn正确.
故选:D.
9.解:(x+m)(x﹣8)=x2+(m﹣8)x﹣8m,
∵(x+m)(x﹣8)=x2+2x+n,
∴m﹣8=2,﹣8m=n,
解得:m=10,n=﹣80,
∴m﹣n=90.
故选:A.
10.解:∵m+n=2,mn=﹣2,
∴(1﹣m)(1﹣n)=1﹣n﹣m+mn=1﹣(n+m)+mn=1﹣2﹣2=﹣3;
故选:C.
11.解:(3x2)2 2x3
=9x4 2x3
=18x7.
故答案为:18x7.
12.解:3×105×5×102=15×107=1.5×108千米.
故答案为:1.5×108.
13.解:(1+x)(1+y)
=1+x+y+xy
∵x+y=3,xy=1,
∴原式=1+3+1
=5.
故答案为:5.
14.解:原式=2x2+6xy﹣xy﹣3y2
=2x2+5xy﹣3y2.
故答案为:2x2+5xy﹣3y2.
15.解:(3﹣ax)(x2+2x﹣1)=(3﹣2a)x2+(a+6)x﹣3﹣ax3,
由展开式中不含x2项,得到3﹣2a=0,
解得:a=,
故答案为:.
16.解:∵=27,
∴(x+1)(x﹣1)﹣(x+2)(x﹣3)=27,
∴x2﹣1﹣(x2﹣x﹣6)=27,
∴x2﹣1﹣x2+x+6=27,
∴x=22;
故答案为:22.
17.解:原式=4a4﹣3a4﹣6a4
=﹣5a4.
18.解:(x+2)(x﹣7)﹣3x
=x2﹣7x+2x﹣14﹣3x
=x2﹣8x﹣14.
19.解:设20222023=a,
那么x=(a﹣1)(a+3)﹣(a+2)a=﹣3,y=a(a+4)﹣(a+1)(a+3)=﹣3,
所以x=y.
20.解:(1)根据题意得:长方形地块的面积=(3a+b)(2a+b)=6a2+5ab+b2,
正方形雕像的面积为:(a﹣b)2=a2﹣2ab+b2,
则绿化面积s=(6a2+5ab+b2)﹣(a2﹣2ab+b2)=5a2+7ab,
即用含a,b的代数式表示绿化面积s=5a2+7ab,
(2)把a=3,b=2代入s=5a2+7ab,
s=5×32+7×3×2=87,
即绿化面积为87平方米.
21.解:(1)由题意得:
(a+b)2=a2+2ab+b2,
故答案为:(a+b)2=a2+2ab+b2;
(2)(a+b)(a+2b)
=a2+3ab+2b2,
故答案为:1,2,3;
(3)设AC=m,BC=n,
由题意得:m+n=6,mn=4,
∴S1+S2=m2+n2=(m+n)2﹣2mn=62﹣2×8=20.
1.计算8a3x3 (﹣2ax)3的结果是( )
A.0 B.﹣64a6x6 C.﹣16a6x6 D.﹣48x4a6
2.小明在做作业的时候,不小心把墨水滴到了作业本上,▄×2ab=4a2b+2ab3,阴影部分即为被墨汁弄污的部分,那么被墨汁遮住的一项是( )
A.(2a+b2) B.(a+2b) C.(3ab+2b2) D.(2ab+b2)
3.计算(﹣2x+1)(﹣3x2)的结果为( )
A.6x3+1 B.6x3﹣3 C.6x3﹣3x2 D.6x3+3x2
4.如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( )
A.﹣3 B.3 C.0 D.1
5.通过计算几何图形的面积可表示一些代数恒等式,右图可表示的代数恒等式是( )
A.(a﹣b)2=a2﹣2ab+b2 B.2a(a+b)=2a2+2ab
C.(a+b)2=a2+2ab+b2 D.(a+b)(a﹣b)=a2﹣b2
6.一个长方体的长、宽、高分别是3m﹣4,2m和m,则它的体积是( )
A.3m3﹣4m2 B.3m2﹣4m3 C.6m3﹣8m2 D.6m2﹣8m3
7.如图,正方形卡片A类,B类和长方形卡片C类若干张,如果要拼一个长为(a+2b),宽为(3a+b)的大长方形,则需要C类卡片( )张.
A.5 B.6 C.7 D.8
8.如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式,你认为其中正确的有( )
①(2a+b)(m+n); ②2a(m+n)+b(m+n);
③m(2a+b)+n(2a+b);④2am+2an+bm+bn.
A.①② B.③④ C.①②③ D.①②③④
9.若(x+m)(x﹣8)=x2+2x+n,则代数式m﹣n的值为( )
A.90 B.﹣70 C.﹣90 D.58
10.已知m+n=2,mn=﹣2,则(1﹣m)(1﹣n)的值为( )
A.﹣1 B.1 C.﹣3 D.5
11.计算:(3x2)2 2x3= .
12.光的速度每秒约3×105千米,太阳光射到地球上需要的时间约是5×102秒,则地球与太阳的距离约是 千米.
13.若x+y=3且xy=1,则代数式(1+x)(1+y)= .
14.化简:(2x﹣y)(x+3y)= .
15.关于x的代数式(3﹣ax)(x2+2x﹣1)的展开式中不含x2项,则a= .
16.对于实数a,b,c,d,规定一种运算=ad﹣bc,如=1×(﹣2)﹣0×2=﹣2,那么当=27时,则x= .
17.计算:(﹣2a2)2﹣3a4+2a (﹣3a3)
18.计算:(x+2)(x﹣7)﹣3x.
19.先阅读材料,再解答问题:
例:已知x=123456789×123456786,y=123456788×123456787,试比较x、y的大小.
解:设123456788=a,则x=(a+1)(a﹣2)=a2﹣a﹣2,y=a(a﹣1)=a2﹣a,
∵x﹣y=(a2﹣a﹣2)﹣(a2﹣a)=﹣2,∴x<y.
问题:已知x=20222022×20222026﹣20222023×20222025,
y=20222023×20222027﹣20222024×20222026,试比较x、y的大小.
20.某市有一块长为3a+b米,宽为2a+b米的长方形地块,规划部门计划将阴影部分进行绿化中间修建一座边长是(a﹣b)的正方形雕像.
(1)请用含a,b的代数式表示绿化面积s;
(2)当a=3,b=2时,求绿化面积.
21.数学活动课上,老师用图①中的1张边长为a的正方形A、1张边长为b的正方形B和2张宽和长分别为a与b的长方形C纸片,排成了如图②中的大正方形.观察图形并解答下列问题.
(1)由图①和图②可以得到的等式为 (用含a,b的代数式表示);
(2)小芳想用图①的三种纸片拼出一个面积为(a+b)(a+2b)的大长方形,则需要A纸片 张,B纸片 张,C纸片 张(空格处填写数字),并尝试在框线中参考图②画出相关的设计图;
(3)如图③,已知点C为线段AB上的动点,分别以AC、BC为边在AB的两侧作正方形ACED和正方形BCFG,面积分别记作S1、S2,若AB=6,图中阴影部分△ACF的面积为4,利用(1)中得到的结论求S1+S2的值.
参考答案
1.解:8a3x3 (﹣2ax)3=8a3x3 (﹣8a3x3)=﹣64a6x6.
故选:B.
2.解:被墨汁遮住部分=(4a2b+2ab3)÷2ab=4a2b÷2ab+2ab3÷2ab=2a+b2,
故选:A.
3.解:原式=6x3﹣3x2.
故选:C.
4.解:∵(x+m)(x+3)=x2+3x+mx+3m=x2+(3+m)x+3m,
又∵(x+m)与(x+3)的乘积中不含x的一次项,
∴3+m=0,
解得m=﹣3.
故选:A.
5.解:长方形的面积等于:2a(a+b),
也等于四个小图形的面积之和:a2+a2+ab+ab=2a2+2ab,
即2a(a+b)=2a2+2ab.
故选:B.
6.解:根据长方体体积的计算公式得,(3m﹣4) 2m m=6m3﹣8m2,
故选:C.
7.解:∵(a+2b)(3a+b)
=3a2+7ab+2b2
∵一张C类卡片的面积为ab
∴需要C类卡片7张.
故选:C.
8.解:表示该长方形面积的多项式
①(2a+b)(m+n)正确;
②2a(m+n)+b(m+n)正确;
③m(2a+b)+n(2a+b)正确;
④2am+2an+bm+bn正确.
故选:D.
9.解:(x+m)(x﹣8)=x2+(m﹣8)x﹣8m,
∵(x+m)(x﹣8)=x2+2x+n,
∴m﹣8=2,﹣8m=n,
解得:m=10,n=﹣80,
∴m﹣n=90.
故选:A.
10.解:∵m+n=2,mn=﹣2,
∴(1﹣m)(1﹣n)=1﹣n﹣m+mn=1﹣(n+m)+mn=1﹣2﹣2=﹣3;
故选:C.
11.解:(3x2)2 2x3
=9x4 2x3
=18x7.
故答案为:18x7.
12.解:3×105×5×102=15×107=1.5×108千米.
故答案为:1.5×108.
13.解:(1+x)(1+y)
=1+x+y+xy
∵x+y=3,xy=1,
∴原式=1+3+1
=5.
故答案为:5.
14.解:原式=2x2+6xy﹣xy﹣3y2
=2x2+5xy﹣3y2.
故答案为:2x2+5xy﹣3y2.
15.解:(3﹣ax)(x2+2x﹣1)=(3﹣2a)x2+(a+6)x﹣3﹣ax3,
由展开式中不含x2项,得到3﹣2a=0,
解得:a=,
故答案为:.
16.解:∵=27,
∴(x+1)(x﹣1)﹣(x+2)(x﹣3)=27,
∴x2﹣1﹣(x2﹣x﹣6)=27,
∴x2﹣1﹣x2+x+6=27,
∴x=22;
故答案为:22.
17.解:原式=4a4﹣3a4﹣6a4
=﹣5a4.
18.解:(x+2)(x﹣7)﹣3x
=x2﹣7x+2x﹣14﹣3x
=x2﹣8x﹣14.
19.解:设20222023=a,
那么x=(a﹣1)(a+3)﹣(a+2)a=﹣3,y=a(a+4)﹣(a+1)(a+3)=﹣3,
所以x=y.
20.解:(1)根据题意得:长方形地块的面积=(3a+b)(2a+b)=6a2+5ab+b2,
正方形雕像的面积为:(a﹣b)2=a2﹣2ab+b2,
则绿化面积s=(6a2+5ab+b2)﹣(a2﹣2ab+b2)=5a2+7ab,
即用含a,b的代数式表示绿化面积s=5a2+7ab,
(2)把a=3,b=2代入s=5a2+7ab,
s=5×32+7×3×2=87,
即绿化面积为87平方米.
21.解:(1)由题意得:
(a+b)2=a2+2ab+b2,
故答案为:(a+b)2=a2+2ab+b2;
(2)(a+b)(a+2b)
=a2+3ab+2b2,
故答案为:1,2,3;
(3)设AC=m,BC=n,
由题意得:m+n=6,mn=4,
∴S1+S2=m2+n2=(m+n)2﹣2mn=62﹣2×8=20.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
