2021-2022学年人教版八年级数学下册17.1勾股定理 同步自主提升训练(Word版 含解析)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册17.1勾股定理 同步自主提升训练(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 241.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 08:45:16 | ||
图片预览


文档简介
2021-2022学年人教版八年级数学下册《17-1勾股定理》同步自主提升训练(附答案)
1.Rt△ABC中,∠C=90°,若a=5,c=13,则b= .
2.如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC、BC为直径作半圆,面积分别记为S1、S2,则S1+S2等于 .
3.直角三角形的两条直角边的长分别是7cm和24cm,则斜边的长是 cm.
4.在Rt△ABC中,∠ACB=90°,AC=12,斜边AB=15,则有另一边BC= .
5.在Rt△ABC中,∠C=90°,CD是斜边AB上的高,AC=8,BC=6,则BD= .
6.如图,△ABC中,∠C=90°,∠1=∠B,CD=5,BD=13,则AC= .
7.如图是由三个正方形和一个直角三角形组成的图形,正方形中的数字均表示该正方形的面积.则正方形A的边长是 .
8.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AC=2,AB=3,则CD为 .
9.如图是在北京召开的国际数学家大会的会标,它是由四个相同的直角三角形与中间一个小正方形拼成的一个大正方形.若每个直角三角形较短的一条直角边长为5cm,小正方形边长为7cm,则大正方形的边长是 cm.
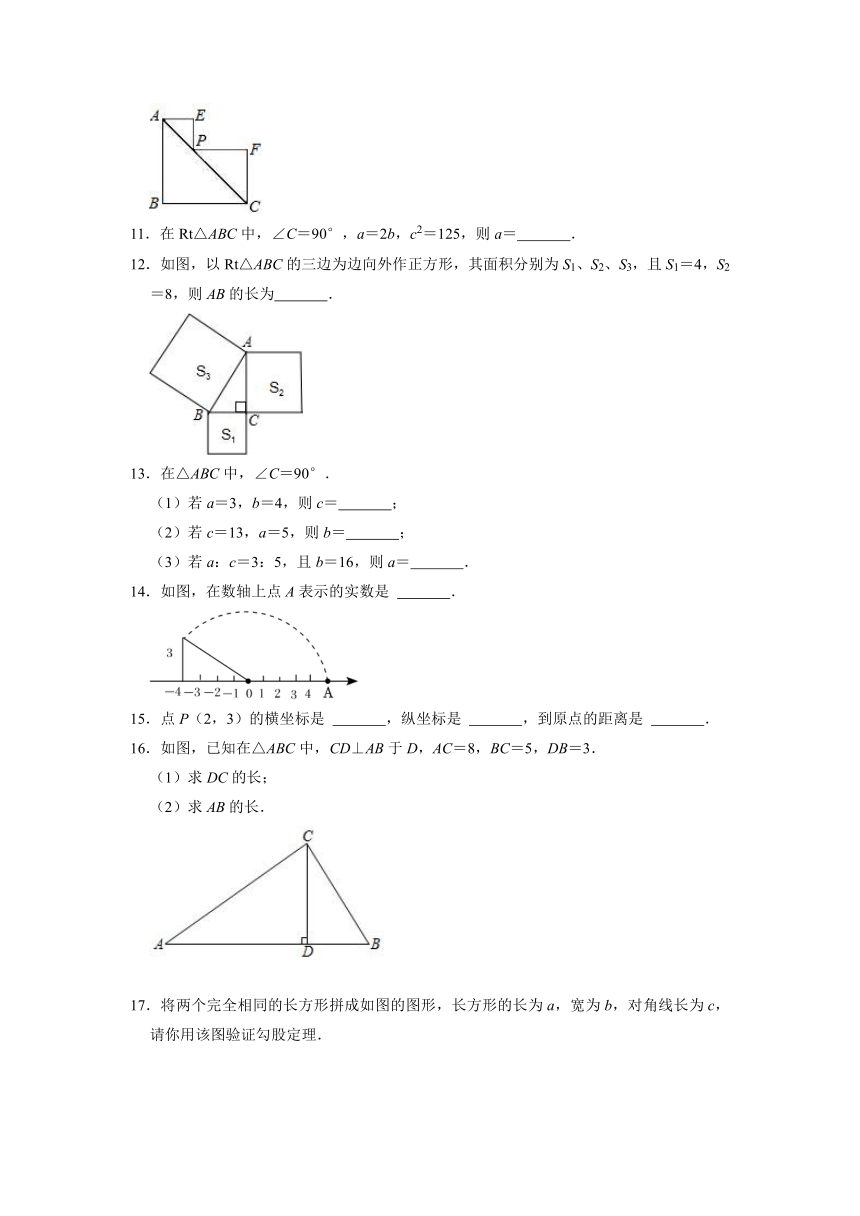
10.已知三个大小不同的等腰直角三角形如图摆放,其中P点在斜边AC上,AP=PF=,则边BC的长为 .
11.在Rt△ABC中,∠C=90°,a=2b,c2=125,则a= .
12.如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S1=4,S2=8,则AB的长为 .
13.在△ABC中,∠C=90°.
(1)若a=3,b=4,则c= ;
(2)若c=13,a=5,则b= ;
(3)若a:c=3:5,且b=16,则a= .
14.如图,在数轴上点A表示的实数是 .
15.点P(2,3)的横坐标是 ,纵坐标是 ,到原点的距离是 .
16.如图,已知在△ABC中,CD⊥AB于D,AC=8,BC=5,DB=3.
(1)求DC的长;
(2)求AB的长.
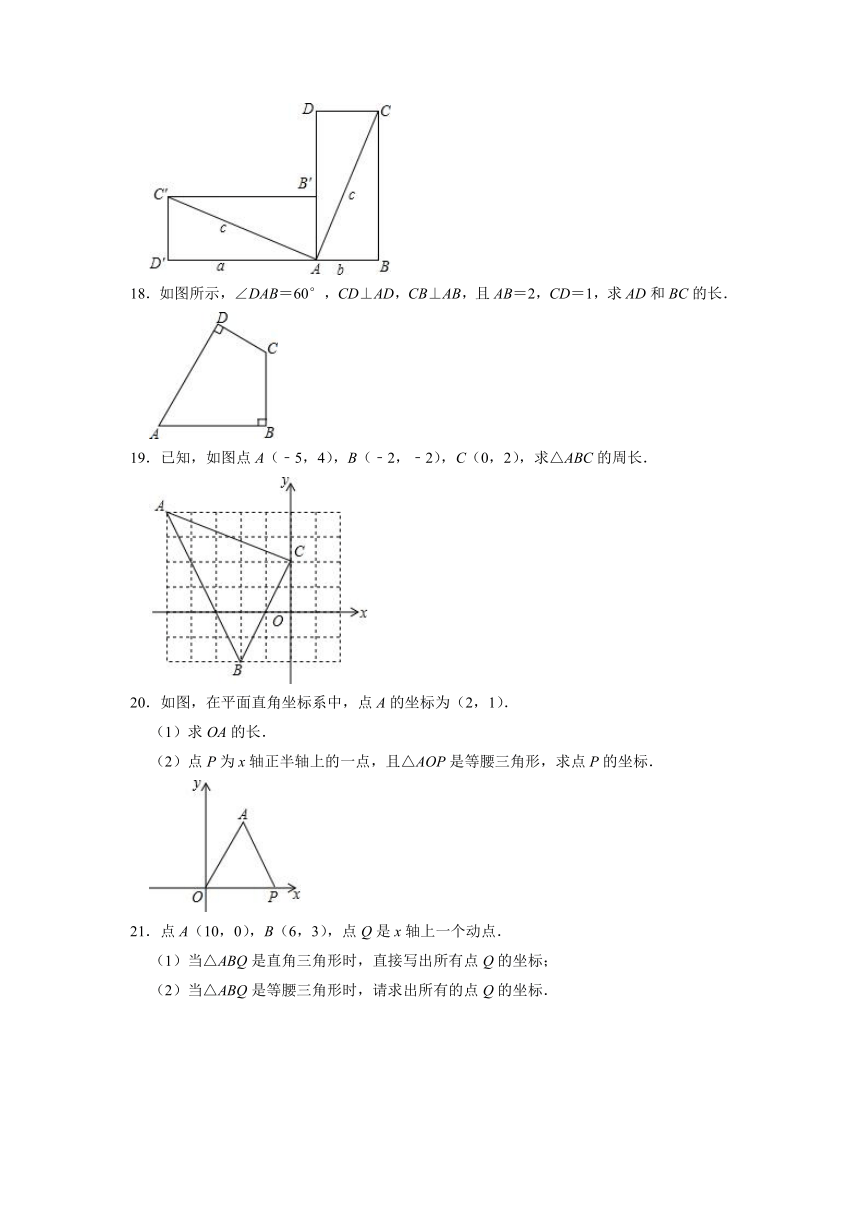
17.将两个完全相同的长方形拼成如图的图形,长方形的长为a,宽为b,对角线长为c,请你用该图验证勾股定理.
18.如图所示,∠DAB=60°,CD⊥AD,CB⊥AB,且AB=2,CD=1,求AD和BC的长.
19.已知,如图点A(﹣5,4),B(﹣2,﹣2),C(0,2),求△ABC的周长.
20.如图,在平面直角坐标系中,点A的坐标为(2,1).
(1)求OA的长.
(2)点P为x轴正半轴上的一点,且△AOP是等腰三角形,求点P的坐标.
21.点A(10,0),B(6,3),点Q是x轴上一个动点.
(1)当△ABQ是直角三角形时,直接写出所有点Q的坐标;
(2)当△ABQ是等腰三角形时,请求出所有的点Q的坐标.
参考答案
1.解:根据勾股定理,得:b===12.
故答案为:12.
2.解:S1=π()2=πAC2,S2=πBC2,
所以S1+S2=π(AC2+BC2)=πAB2=2π.
故答案为:2π.
3.解:∵直角三角形的两条直角边的长分别是7cm和24cm,
∴斜边长==25cm.
故答案为25cm.
4.解:在Rt△ABC中,∠ACB=90°,
则有AC2+BC2=AB2,
∵AB=15,AC=12,
则BC====9.
故答案为9.
5.解:直角△ABC中,AC=8,BC=6,所以62+82=AB2,解得:AB=10,
Rt△ABC的面积为:×AC×BC=,所以CD=4.8.
在Rt△CDB中,BD2=BC2﹣CD2,解得:BD=3.6.
6.解:∵∠1=∠B,
∴AD=BD=13.
在直角三角形ACD中,根据勾股定理,得
AC=12.
7.解:直角三角形的斜边的平方=400+225=625,
∴正方形A的边长==25.
故答案为:25.
8.解:根据题意得:BC===.
∵△ABC的面积= AC BC= AB CD
∴CD===2.
9.解:直角三角形的长直角边=短直角边+小正方形的边长=12cm,
∴大正方形的边长==13cm.
故答案为:13.
10.解:在等腰直角△PFC中,因为PF=,
所以PC2=2×PF2,即PC=2
所以AC=AP+PC=2+
在等腰直角△ABC中,根据勾股定理得:BC=1+.
11.解:在直角三角形ABC中,
∵∠C=90°,∴c为斜边,
根据勾股定理,c2=a2+b2,且a=2b,c2=125,
解得:b=5,a=10,
故a=10.
12.解:∵S1=4,∴BC2=4,
∵S2=8,∴AC2=8,
∴在Rt△ABC中,BC2+AC2=AB2,
∴AB=2.
13.解:(1)由勾股定理得:c==5,
故答案为:5;
(2)由勾股定理得:b==12,
故答案为:12;
(3)设a=3x,c=5x,由勾股定理得:(3x)2+162=(5x)2,
解得:x=±4(负值舍去),
∴a=12,
故答案为:12.
14.解:由勾股定理得:OA2=32+42=25,
∴OA=5,
∴在数轴上点A表示的实数是5,
故答案为:5.
15.解:如图,
∵点P(2,3),
∴点P的横坐标是2,纵坐标是3,AO=2,AP=3,
∴OP===,
∴点P到原点的距离是,
故答案为:2;3;.
16.解:(1)∵CD⊥AB于D,BC=5,DB=3,
∴在Rt△BCD中,CD2=CB2﹣DB2=52﹣32=16,
∴CD=4.
(2)在Rt△ACD中,AD2=AC2﹣CD2=82﹣42=48,
∴AD=4,
∴AB=AD+DB=4+3.
17.证明:如图,连接CC′,
∵S梯形D′C′CB=(C′D′+BC) BD′=(a+b) (a+b)=(a+b)2,
∵Rt△C′D′A≌Rt△CDA,
∴∠C′AD′=∠CAD,
∵∠C′AD′+∠C′AB′=90°,
∴∠C′AB′+∠CAD,
即∠C′AC=90°,
∵S梯形D′C′CB=S△AC′D′+S△ACC′+S△ABC,
∴S梯形D′C′CB=ab+ab+c2,
∴(a+b)2=ab+ab+c2
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
18.解:延长AB,DC相交于点E,
∵∠DAB=60°,CD⊥AD,CB⊥AB,
∴∠E=30°.
设BC=x,则CE=2x,BE=x,
同理,在Rt△ADE中,AD=AE=(2+x),DE=CD+CE=1+2x=AE ,即1+2x=(2+x) ,
∴x=﹣1,
∴AD=AE=[1+(﹣1)]=2﹣;
BC=﹣1.
19.解:∵AC==,
BC==2,
AB==3,
∴△ABC的周长为+2+3=+5.
20.解:(1)如图1,作AE⊥x轴,
∵点A的坐标为(2,1),
∴OE=2,AE=1,
∴OA==.
(2)根据等腰三角形的性质可知,P1(4,0),P2(,0),
设OA解析式为y=kx,
把(2,1)代入解析式得,
1=2k,解得k=,
则解析式为y=x,B点坐标为(,),即B(1,).
设BP3解析式为y=﹣2x+b,把B(1,)代入解析式得=﹣2+b,
解得b=2+=,
则解析式为y=﹣2x+,
当y=0时,﹣2x+=0,解得x=,P3(,0).
21.解:(1)分两种情况:如图1所示:
①当∠AQB=90°时,
点Q的坐标为(6,0);
当∠ABQ=90°时,
点Q的坐标为(,0);
综上所述:点Q的坐标为(6,0)或(,0);
(2)作BD⊥x轴于D,如图2所示:
则∠BDA=90°,OD=6,OA=10,BD=3,
∴AD=4,
∴AB==5,
分三种情况:
①当BQ=BA时,DQ=AD=4,
∴OQ=2,
∴Q(2,0);
②当AQ=AB时,OQ=5,或OQ=15,
∴Q(5,0),或(15,0);
③当AQ=BQ时,Q在AB的垂直平分线上,
点Q的坐标为(,0);
综上所述:点Q的坐标为(2,0)或(5,0)或(15,0)或(,0).
1.Rt△ABC中,∠C=90°,若a=5,c=13,则b= .
2.如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC、BC为直径作半圆,面积分别记为S1、S2,则S1+S2等于 .
3.直角三角形的两条直角边的长分别是7cm和24cm,则斜边的长是 cm.
4.在Rt△ABC中,∠ACB=90°,AC=12,斜边AB=15,则有另一边BC= .
5.在Rt△ABC中,∠C=90°,CD是斜边AB上的高,AC=8,BC=6,则BD= .
6.如图,△ABC中,∠C=90°,∠1=∠B,CD=5,BD=13,则AC= .
7.如图是由三个正方形和一个直角三角形组成的图形,正方形中的数字均表示该正方形的面积.则正方形A的边长是 .
8.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AC=2,AB=3,则CD为 .
9.如图是在北京召开的国际数学家大会的会标,它是由四个相同的直角三角形与中间一个小正方形拼成的一个大正方形.若每个直角三角形较短的一条直角边长为5cm,小正方形边长为7cm,则大正方形的边长是 cm.
10.已知三个大小不同的等腰直角三角形如图摆放,其中P点在斜边AC上,AP=PF=,则边BC的长为 .
11.在Rt△ABC中,∠C=90°,a=2b,c2=125,则a= .
12.如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S1=4,S2=8,则AB的长为 .
13.在△ABC中,∠C=90°.
(1)若a=3,b=4,则c= ;
(2)若c=13,a=5,则b= ;
(3)若a:c=3:5,且b=16,则a= .
14.如图,在数轴上点A表示的实数是 .
15.点P(2,3)的横坐标是 ,纵坐标是 ,到原点的距离是 .
16.如图,已知在△ABC中,CD⊥AB于D,AC=8,BC=5,DB=3.
(1)求DC的长;
(2)求AB的长.
17.将两个完全相同的长方形拼成如图的图形,长方形的长为a,宽为b,对角线长为c,请你用该图验证勾股定理.
18.如图所示,∠DAB=60°,CD⊥AD,CB⊥AB,且AB=2,CD=1,求AD和BC的长.
19.已知,如图点A(﹣5,4),B(﹣2,﹣2),C(0,2),求△ABC的周长.
20.如图,在平面直角坐标系中,点A的坐标为(2,1).
(1)求OA的长.
(2)点P为x轴正半轴上的一点,且△AOP是等腰三角形,求点P的坐标.
21.点A(10,0),B(6,3),点Q是x轴上一个动点.
(1)当△ABQ是直角三角形时,直接写出所有点Q的坐标;
(2)当△ABQ是等腰三角形时,请求出所有的点Q的坐标.
参考答案
1.解:根据勾股定理,得:b===12.
故答案为:12.
2.解:S1=π()2=πAC2,S2=πBC2,
所以S1+S2=π(AC2+BC2)=πAB2=2π.
故答案为:2π.
3.解:∵直角三角形的两条直角边的长分别是7cm和24cm,
∴斜边长==25cm.
故答案为25cm.
4.解:在Rt△ABC中,∠ACB=90°,
则有AC2+BC2=AB2,
∵AB=15,AC=12,
则BC====9.
故答案为9.
5.解:直角△ABC中,AC=8,BC=6,所以62+82=AB2,解得:AB=10,
Rt△ABC的面积为:×AC×BC=,所以CD=4.8.
在Rt△CDB中,BD2=BC2﹣CD2,解得:BD=3.6.
6.解:∵∠1=∠B,
∴AD=BD=13.
在直角三角形ACD中,根据勾股定理,得
AC=12.
7.解:直角三角形的斜边的平方=400+225=625,
∴正方形A的边长==25.
故答案为:25.
8.解:根据题意得:BC===.
∵△ABC的面积= AC BC= AB CD
∴CD===2.
9.解:直角三角形的长直角边=短直角边+小正方形的边长=12cm,
∴大正方形的边长==13cm.
故答案为:13.
10.解:在等腰直角△PFC中,因为PF=,
所以PC2=2×PF2,即PC=2
所以AC=AP+PC=2+
在等腰直角△ABC中,根据勾股定理得:BC=1+.
11.解:在直角三角形ABC中,
∵∠C=90°,∴c为斜边,
根据勾股定理,c2=a2+b2,且a=2b,c2=125,
解得:b=5,a=10,
故a=10.
12.解:∵S1=4,∴BC2=4,
∵S2=8,∴AC2=8,
∴在Rt△ABC中,BC2+AC2=AB2,
∴AB=2.
13.解:(1)由勾股定理得:c==5,
故答案为:5;
(2)由勾股定理得:b==12,
故答案为:12;
(3)设a=3x,c=5x,由勾股定理得:(3x)2+162=(5x)2,
解得:x=±4(负值舍去),
∴a=12,
故答案为:12.
14.解:由勾股定理得:OA2=32+42=25,
∴OA=5,
∴在数轴上点A表示的实数是5,
故答案为:5.
15.解:如图,
∵点P(2,3),
∴点P的横坐标是2,纵坐标是3,AO=2,AP=3,
∴OP===,
∴点P到原点的距离是,
故答案为:2;3;.
16.解:(1)∵CD⊥AB于D,BC=5,DB=3,
∴在Rt△BCD中,CD2=CB2﹣DB2=52﹣32=16,
∴CD=4.
(2)在Rt△ACD中,AD2=AC2﹣CD2=82﹣42=48,
∴AD=4,
∴AB=AD+DB=4+3.
17.证明:如图,连接CC′,
∵S梯形D′C′CB=(C′D′+BC) BD′=(a+b) (a+b)=(a+b)2,
∵Rt△C′D′A≌Rt△CDA,
∴∠C′AD′=∠CAD,
∵∠C′AD′+∠C′AB′=90°,
∴∠C′AB′+∠CAD,
即∠C′AC=90°,
∵S梯形D′C′CB=S△AC′D′+S△ACC′+S△ABC,
∴S梯形D′C′CB=ab+ab+c2,
∴(a+b)2=ab+ab+c2
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
18.解:延长AB,DC相交于点E,
∵∠DAB=60°,CD⊥AD,CB⊥AB,
∴∠E=30°.
设BC=x,则CE=2x,BE=x,
同理,在Rt△ADE中,AD=AE=(2+x),DE=CD+CE=1+2x=AE ,即1+2x=(2+x) ,
∴x=﹣1,
∴AD=AE=[1+(﹣1)]=2﹣;
BC=﹣1.
19.解:∵AC==,
BC==2,
AB==3,
∴△ABC的周长为+2+3=+5.
20.解:(1)如图1,作AE⊥x轴,
∵点A的坐标为(2,1),
∴OE=2,AE=1,
∴OA==.
(2)根据等腰三角形的性质可知,P1(4,0),P2(,0),
设OA解析式为y=kx,
把(2,1)代入解析式得,
1=2k,解得k=,
则解析式为y=x,B点坐标为(,),即B(1,).
设BP3解析式为y=﹣2x+b,把B(1,)代入解析式得=﹣2+b,
解得b=2+=,
则解析式为y=﹣2x+,
当y=0时,﹣2x+=0,解得x=,P3(,0).
21.解:(1)分两种情况:如图1所示:
①当∠AQB=90°时,
点Q的坐标为(6,0);
当∠ABQ=90°时,
点Q的坐标为(,0);
综上所述:点Q的坐标为(6,0)或(,0);
(2)作BD⊥x轴于D,如图2所示:
则∠BDA=90°,OD=6,OA=10,BD=3,
∴AD=4,
∴AB==5,
分三种情况:
①当BQ=BA时,DQ=AD=4,
∴OQ=2,
∴Q(2,0);
②当AQ=AB时,OQ=5,或OQ=15,
∴Q(5,0),或(15,0);
③当AQ=BQ时,Q在AB的垂直平分线上,
点Q的坐标为(,0);
综上所述:点Q的坐标为(2,0)或(5,0)或(15,0)或(,0).
