小学数学 人教版 五年级上册 7 数学广角—《植树问题》(教案)
文档属性
| 名称 | 小学数学 人教版 五年级上册 7 数学广角—《植树问题》(教案) |

|
|
| 格式 | doc | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 00:00:00 | ||
图片预览



文档简介
植树问题
【教学内容】:人教版小学数学五年级上册P106-P107页例1、例2
【设计理念】:数学课程标准指出:“认真听讲、积极思考、动手实践、自主探索、合作交流等,都是学习数学的重要方式。”本设计从简单问题入手,通过学生的动手操作,自己种一种,去发现探讨植树问题中蕴含的规律,建构数学模型,“植树问题”中的“树”可以换成其他事物吗?什么情况下也可以用“植树问题”的知识解决?学生经历建构模型、寻找结果、解决问题的过程,提高学生学习数学的兴趣。
【教材分析】:教材出示示意图,因当数据比较大时,不利于学生发现规律,所以教材在编排上体现了化繁为简和建模的思想,让学生先研究20米长的路,30米、35米等,通过两个小朋友的对话,告诉学生用画示意图或者线段图的方法帮助思考,由简单的问题入手,探讨了两段都栽的情况下,棵数与间隔数的规律,在通过发散思维,探讨两端不栽、只栽一端的情况。
【学情分析】:五年级的学生,具备一定的生活经验,动手能力也比较强了,但对于数学模型的建构经历就比较欠缺。他们不会把问题归类,对于事物中蕴含的规律,缺乏发现的眼光,需要老师引导经历建构模型、寻找结果、解决问题的过程。
【教学目标】:
知识与技能
1.利用学生熟悉的生活情境,通过动手操作的实践活动,让学生发现间隔数与植树棵数之间的关系。
2.通过小组合作、交流,使学生能理解间隔数与植树棵数之间的规律。
3.能够借助图形,利用规律来解决简单植树的问题。
过程与方法
1.进一步培养学生从实际问题中发现规律,应用规律解决问题的能力。
2.渗透数形结合的思想,培养学生借助图形解决问题的意识。
3.培养学生的合作意识,养成良好的交流习惯。
情感态度与价值观
通过实践活动激发热爱数学的情感,感受日常生活中处处有数学、体验学习成功的喜悦。
【教学重点】:理解种树棵数与间隔数之间的关系。
【教学难点】:灵活应用发现的规律解决一些相关的实际问题。
一、观看视频,引入课题
观看公益广告 《植树造林》,说说植树有什么好处?其实,植树也蕴含着很多的数学知识, 我们今天就来研究植树问题。(板书课题:植树问题)
1.一条20米长的路,每5米分一段,共分几段?
2.一条20米长的路,在路的一旁,每隔5米栽一棵树,共栽几棵树?
二、探究新知
1.小组合作设计植树方案。
理解题意:什么是“一边植树”?什么又是“每隔5米栽一棵”呢?
(1)学生小组合作,利用准备的学具模拟植树。
(2)学生汇报方案,学生用实物模拟植树
学生汇报并板演第一种设计方案。
我们一共种了5棵树,这5棵树把这条路分成了4段。
学生汇报并板演第二种设计方案。
师提问:这种情况符合我们的要求吗?什么情况下会遇到这种情况?(可以在小路的一端贴上房子 )当我们一端有障碍物的时候,就会出现这种情况。
学生汇报并板演第三种设计方案。
师提问:这种情况符合我们的要求吗?什么情况下会遇到这种情况?(可以在小路的两端贴上房子 )当我们两端都有障碍物的时候,就会出现这种情况。
同学们真棒,通过自己动手,找出了我们的答案,我们仔细观察,这三种情况,隐藏着什么样的奥秘?
2.探究间隔数的算法。
师:三种不同的栽法有什么相同之处?(引导发现都是在20米的小路上植树,都是每隔5米栽一棵,而且都分成4段)小树把小路分成的段数是4段,也就是有4个间隔,间隔数与路长和间隔长有什么关系?要求间隔数必须知道哪两个条件?(引导学生发现20÷5=4(个)也就是间隔数=路长÷ 间隔长)
举例:如果在全长100米的小路一边植树,每隔10米栽一棵。一共有多少个间隔?每隔20米栽一棵,一共有多少个间隔?
板书:间隔数=路长÷间隔长
师:三种不同的栽法有什么不同之处?(引导发现所需的棵树不同,有的5棵,有的4棵,有的3棵.)
板书:两端都栽 只栽一端 两端都不栽
师:看来,已知条件相同,但是植树要求不同,就会出现不同的结果。
3.探究、验证间隔数与棵树之间的关系
师:那间隔数与棵树之间有怎样的关系呢?我们一起来研究。
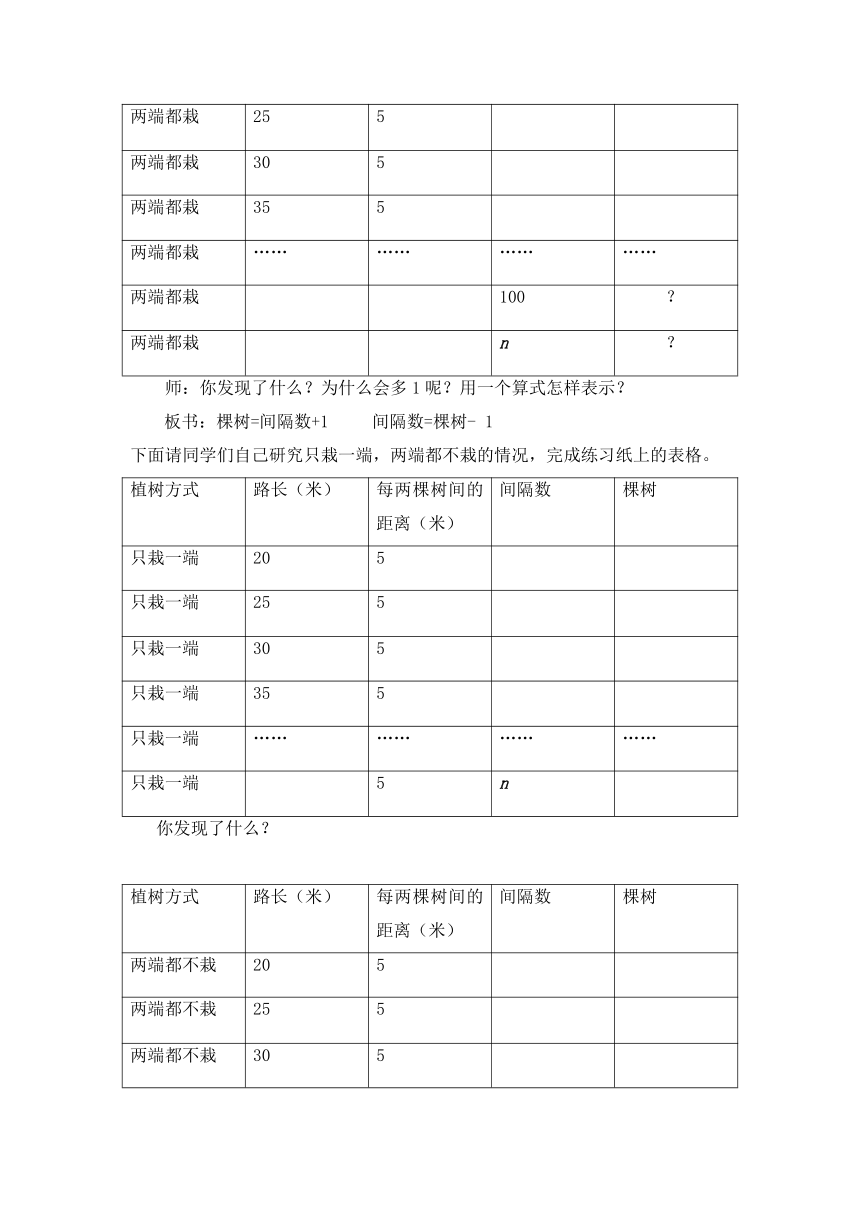
植树方式 路长(米) 每两棵树间的距离(米) 间隔数 棵树
两端都栽 20 5
两端都栽 25 5
两端都栽 30 5
两端都栽 35 5
两端都栽 …… …… …… ……
两端都栽 100 ?
两端都栽 n ?
师:你发现了什么?为什么会多1呢?用一个算式怎样表示?
板书:棵树=间隔数+1 间隔数=棵树- 1
下面请同学们自己研究只栽一端,两端都不栽的情况,完成练习纸上的表格。
植树方式 路长(米) 每两棵树间的距离(米) 间隔数 棵树
只栽一端 20 5
只栽一端 25 5
只栽一端 30 5
只栽一端 35 5
只栽一端 …… …… …… ……
只栽一端 5 n
你发现了什么?
植树方式 路长(米) 每两棵树间的距离(米) 间隔数 棵树
两端都不栽 20 5
两端都不栽 25 5
两端都不栽 30 5
两端都不栽 35 5
两端都不栽 …… …… …… ……
两端都不栽 5 n
你发现了什么?
学生汇报
【设计意图:让学生经历探索的过程,自己寻找规律,体现学生是学习活动的主体,教师是学习活动的引导者,在动手操作过程中,培养学生的动手能力、观察能力、发现问题的能力。】
4.利用规律,解决问题
师:原来植树当中还有那么多的规律,现在就让我们带着规律去解决问题吧。 (1)例1:同学们要在一条全长100米的公路一旁植树,每隔5米种一棵(两端要种)。一共需要多少棵树苗?
学生独立解答:100÷5=20(个)
20+1=21(棵)
答:一共需要21棵树苗。
例2: 动物园的大象馆和猩猩馆相距60米,绿化队要在两馆间的小路两旁栽树,相邻两棵树之间的距离是3米,一共要栽几棵树
师:这道题属于我们今天学习的植树问题中三个类型中的哪一类?你觉得题目中哪些地方需要注意的?自己动手算一下。
60÷3=20(个)
20-1=19(棵)
19×2=38(棵)
答:一共要栽38棵树。
5.在“植树问题”中,一定要是“树”吗?除了“树”,还能换成别的事物吗?
【设计意图:帮助学生建立数学模型,发展学生的数学思维,不局限于仅仅植树,帮助学生总结在什么情况下可以应用植树问题的规律解决问题。】
三、巩固知识
1.为迎接元旦,学校准备在教学楼前60米的道路两旁摆放鲜花(靠墙一端不放),相邻两盆花之间的距离3米。一共需要几盆花?
①20 ②19 ③40
2.一根木头,要把它平均分成5段。每锯下一段需要8分钟,锯完一共要花多少分钟?
①40 ②32 ③48
3.同学们大课间队列,其中一列纵队站了25人,每相邻两人之间的距离是1.2米,这一列纵队,从第一个人到最后一个人 距离有多远?
【设计意图:设计的练习具有代表性,层层递进,通过抢答,复习植树问题中的棵数与间隔数的关系,巩固知识,同时激发学生学习的兴趣,第3道题,从学生生活经验出发,逆用植树问题的规律,多方面发展学生的思维。】
四、观看微课,了解数学难题
著名的二十棵树植树问题
数学史上有个20棵树植树问题,几个世纪以来一直享誉全球,不断给人类智慧的滋养,聪明的启迪。20棵树植树问题,简单地说,就是:有20棵树,若每行四棵,问怎样种植(组排),才能使行数更多?20棵树植树问题,早在十六世纪,古希腊、古罗马、古埃及等都先后完成了十六行的排列并将美丽的图谱广泛应用于高雅装饰建筑、华丽工艺美术(图1)。进入十八世纪,德国数学家高斯猜想20棵树植树问题应能达到十八行,但一直未能见其发表绘制出的十八行图谱。直到十九世纪,此猜想才被美国的娱乐数学大师山姆·劳埃德完成并绘制出了精美的十八行图谱。 进入20世纪七十年代,两位数学爱好者巧妙地运用电子计算机超越了数学大师山姆·劳埃德保持的十八行纪录,成功地绘制出了精湛美丽的二十行图谱,创造了20棵树植树问题新世纪的新纪录并保持至今(图3)。跨入21世纪,20棵树植树问题又被数学家们从新提出:20棵树,每行四棵,还能有更新的进展吗?数学界正翘首以待。【设计意图:拓展学生的知识面,提高学生学习数学的兴趣,体会数学来源于生活,服务于生活,数学的神奇与奥秘,激励他们努力学习,积极去探讨数学的奥秘。】
五、课堂小结
师:通过这节课的学习,你学会了什么?
六、板书设计:
植树问题
两端都栽 棵树=间隔数+1
两端都不栽 棵树=间隔数- 1
棵树=间隔数
只栽一端
【教学内容】:人教版小学数学五年级上册P106-P107页例1、例2
【设计理念】:数学课程标准指出:“认真听讲、积极思考、动手实践、自主探索、合作交流等,都是学习数学的重要方式。”本设计从简单问题入手,通过学生的动手操作,自己种一种,去发现探讨植树问题中蕴含的规律,建构数学模型,“植树问题”中的“树”可以换成其他事物吗?什么情况下也可以用“植树问题”的知识解决?学生经历建构模型、寻找结果、解决问题的过程,提高学生学习数学的兴趣。
【教材分析】:教材出示示意图,因当数据比较大时,不利于学生发现规律,所以教材在编排上体现了化繁为简和建模的思想,让学生先研究20米长的路,30米、35米等,通过两个小朋友的对话,告诉学生用画示意图或者线段图的方法帮助思考,由简单的问题入手,探讨了两段都栽的情况下,棵数与间隔数的规律,在通过发散思维,探讨两端不栽、只栽一端的情况。
【学情分析】:五年级的学生,具备一定的生活经验,动手能力也比较强了,但对于数学模型的建构经历就比较欠缺。他们不会把问题归类,对于事物中蕴含的规律,缺乏发现的眼光,需要老师引导经历建构模型、寻找结果、解决问题的过程。
【教学目标】:
知识与技能
1.利用学生熟悉的生活情境,通过动手操作的实践活动,让学生发现间隔数与植树棵数之间的关系。
2.通过小组合作、交流,使学生能理解间隔数与植树棵数之间的规律。
3.能够借助图形,利用规律来解决简单植树的问题。
过程与方法
1.进一步培养学生从实际问题中发现规律,应用规律解决问题的能力。
2.渗透数形结合的思想,培养学生借助图形解决问题的意识。
3.培养学生的合作意识,养成良好的交流习惯。
情感态度与价值观
通过实践活动激发热爱数学的情感,感受日常生活中处处有数学、体验学习成功的喜悦。
【教学重点】:理解种树棵数与间隔数之间的关系。
【教学难点】:灵活应用发现的规律解决一些相关的实际问题。
一、观看视频,引入课题
观看公益广告 《植树造林》,说说植树有什么好处?其实,植树也蕴含着很多的数学知识, 我们今天就来研究植树问题。(板书课题:植树问题)
1.一条20米长的路,每5米分一段,共分几段?
2.一条20米长的路,在路的一旁,每隔5米栽一棵树,共栽几棵树?
二、探究新知
1.小组合作设计植树方案。
理解题意:什么是“一边植树”?什么又是“每隔5米栽一棵”呢?
(1)学生小组合作,利用准备的学具模拟植树。
(2)学生汇报方案,学生用实物模拟植树
学生汇报并板演第一种设计方案。
我们一共种了5棵树,这5棵树把这条路分成了4段。
学生汇报并板演第二种设计方案。
师提问:这种情况符合我们的要求吗?什么情况下会遇到这种情况?(可以在小路的一端贴上房子 )当我们一端有障碍物的时候,就会出现这种情况。
学生汇报并板演第三种设计方案。
师提问:这种情况符合我们的要求吗?什么情况下会遇到这种情况?(可以在小路的两端贴上房子 )当我们两端都有障碍物的时候,就会出现这种情况。
同学们真棒,通过自己动手,找出了我们的答案,我们仔细观察,这三种情况,隐藏着什么样的奥秘?
2.探究间隔数的算法。
师:三种不同的栽法有什么相同之处?(引导发现都是在20米的小路上植树,都是每隔5米栽一棵,而且都分成4段)小树把小路分成的段数是4段,也就是有4个间隔,间隔数与路长和间隔长有什么关系?要求间隔数必须知道哪两个条件?(引导学生发现20÷5=4(个)也就是间隔数=路长÷ 间隔长)
举例:如果在全长100米的小路一边植树,每隔10米栽一棵。一共有多少个间隔?每隔20米栽一棵,一共有多少个间隔?
板书:间隔数=路长÷间隔长
师:三种不同的栽法有什么不同之处?(引导发现所需的棵树不同,有的5棵,有的4棵,有的3棵.)
板书:两端都栽 只栽一端 两端都不栽
师:看来,已知条件相同,但是植树要求不同,就会出现不同的结果。
3.探究、验证间隔数与棵树之间的关系
师:那间隔数与棵树之间有怎样的关系呢?我们一起来研究。
植树方式 路长(米) 每两棵树间的距离(米) 间隔数 棵树
两端都栽 20 5
两端都栽 25 5
两端都栽 30 5
两端都栽 35 5
两端都栽 …… …… …… ……
两端都栽 100 ?
两端都栽 n ?
师:你发现了什么?为什么会多1呢?用一个算式怎样表示?
板书:棵树=间隔数+1 间隔数=棵树- 1
下面请同学们自己研究只栽一端,两端都不栽的情况,完成练习纸上的表格。
植树方式 路长(米) 每两棵树间的距离(米) 间隔数 棵树
只栽一端 20 5
只栽一端 25 5
只栽一端 30 5
只栽一端 35 5
只栽一端 …… …… …… ……
只栽一端 5 n
你发现了什么?
植树方式 路长(米) 每两棵树间的距离(米) 间隔数 棵树
两端都不栽 20 5
两端都不栽 25 5
两端都不栽 30 5
两端都不栽 35 5
两端都不栽 …… …… …… ……
两端都不栽 5 n
你发现了什么?
学生汇报
【设计意图:让学生经历探索的过程,自己寻找规律,体现学生是学习活动的主体,教师是学习活动的引导者,在动手操作过程中,培养学生的动手能力、观察能力、发现问题的能力。】
4.利用规律,解决问题
师:原来植树当中还有那么多的规律,现在就让我们带着规律去解决问题吧。 (1)例1:同学们要在一条全长100米的公路一旁植树,每隔5米种一棵(两端要种)。一共需要多少棵树苗?
学生独立解答:100÷5=20(个)
20+1=21(棵)
答:一共需要21棵树苗。
例2: 动物园的大象馆和猩猩馆相距60米,绿化队要在两馆间的小路两旁栽树,相邻两棵树之间的距离是3米,一共要栽几棵树
师:这道题属于我们今天学习的植树问题中三个类型中的哪一类?你觉得题目中哪些地方需要注意的?自己动手算一下。
60÷3=20(个)
20-1=19(棵)
19×2=38(棵)
答:一共要栽38棵树。
5.在“植树问题”中,一定要是“树”吗?除了“树”,还能换成别的事物吗?
【设计意图:帮助学生建立数学模型,发展学生的数学思维,不局限于仅仅植树,帮助学生总结在什么情况下可以应用植树问题的规律解决问题。】
三、巩固知识
1.为迎接元旦,学校准备在教学楼前60米的道路两旁摆放鲜花(靠墙一端不放),相邻两盆花之间的距离3米。一共需要几盆花?
①20 ②19 ③40
2.一根木头,要把它平均分成5段。每锯下一段需要8分钟,锯完一共要花多少分钟?
①40 ②32 ③48
3.同学们大课间队列,其中一列纵队站了25人,每相邻两人之间的距离是1.2米,这一列纵队,从第一个人到最后一个人 距离有多远?
【设计意图:设计的练习具有代表性,层层递进,通过抢答,复习植树问题中的棵数与间隔数的关系,巩固知识,同时激发学生学习的兴趣,第3道题,从学生生活经验出发,逆用植树问题的规律,多方面发展学生的思维。】
四、观看微课,了解数学难题
著名的二十棵树植树问题
数学史上有个20棵树植树问题,几个世纪以来一直享誉全球,不断给人类智慧的滋养,聪明的启迪。20棵树植树问题,简单地说,就是:有20棵树,若每行四棵,问怎样种植(组排),才能使行数更多?20棵树植树问题,早在十六世纪,古希腊、古罗马、古埃及等都先后完成了十六行的排列并将美丽的图谱广泛应用于高雅装饰建筑、华丽工艺美术(图1)。进入十八世纪,德国数学家高斯猜想20棵树植树问题应能达到十八行,但一直未能见其发表绘制出的十八行图谱。直到十九世纪,此猜想才被美国的娱乐数学大师山姆·劳埃德完成并绘制出了精美的十八行图谱。 进入20世纪七十年代,两位数学爱好者巧妙地运用电子计算机超越了数学大师山姆·劳埃德保持的十八行纪录,成功地绘制出了精湛美丽的二十行图谱,创造了20棵树植树问题新世纪的新纪录并保持至今(图3)。跨入21世纪,20棵树植树问题又被数学家们从新提出:20棵树,每行四棵,还能有更新的进展吗?数学界正翘首以待。【设计意图:拓展学生的知识面,提高学生学习数学的兴趣,体会数学来源于生活,服务于生活,数学的神奇与奥秘,激励他们努力学习,积极去探讨数学的奥秘。】
五、课堂小结
师:通过这节课的学习,你学会了什么?
六、板书设计:
植树问题
两端都栽 棵树=间隔数+1
两端都不栽 棵树=间隔数- 1
棵树=间隔数
只栽一端
