华东师大版八年级下册数学 20.3.1 方差 课件(共19张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 20.3.1 方差 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 191.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
方差
课堂引入
在统计学中,除了平均数、中位数、众数这类刻画数据集中趋势的量以外,还有一类刻画数据波动程度的量,其中最重要的就是方差.
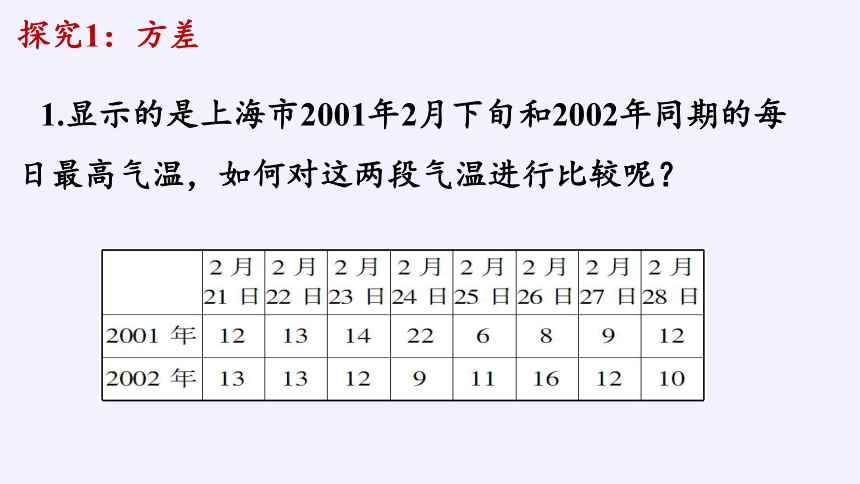
1.显示的是上海市2001年2月下旬和2002年同期的每日最高气温,如何对这两段气温进行比较呢?
探究1:方差
经计算可知这两个时段的平均气温相等,都是12℃,这是不是说,两个时段的气温情况总体上没有什么差异呢?
探究1:方差
观察下图,你感觉它们有没有差异呢?
通过观察,我们可以发现,图(A)中的点的波动范围比图(B)中的点波动范围要大.
图(A)中温度的最大值与最小值之间的差距很大,相差16℃,图(B)中温度的最大值与最小值相差7℃,由此,我们可以判定2001年同期气温波动范围要大.
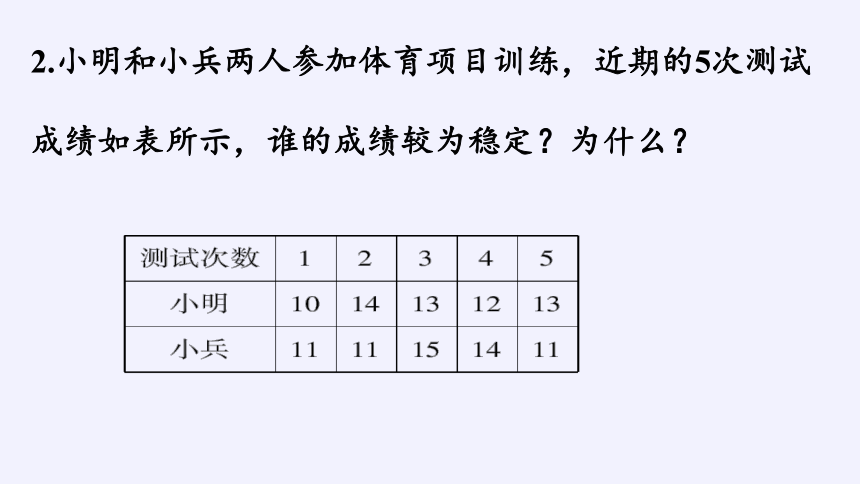
2.小明和小兵两人参加体育项目训练,近期的5次测试成绩如表所示,谁的成绩较为稳定?为什么?
解:通过计算分析,两人测试成绩的平均数都是12.4,成绩的最大值与最小值也都相差4,但从下图中我们可以看到:相比下,小明的成绩大部分集中在平均数附近,而小兵的成绩与其平均数的离散程度略大.
通常,如果一组数据与其平均数的离散程度较小,我们就说它比较稳定.
那么,怎样的指标能反映一组数据与其平均数的离散程度呢?
统计学中常采用下面的做法来量化这组数据的波动大小:
设有n个数据x1,x2,…,xn,各数据与它们的平均
数 的差的平方分别是 ,
我们用这些值的平均数,即用
来衡量这组数据的波动大小,称它为这组数据的方差.
探究新知
方差越大,数据的波动越大;
方差越小,数据的波动越小.
探究新知
例1 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm),如表所示.
应用举例
甲 163 164 164 165 165 165 166 167
乙 163 164 164 165 166 167 167 168
哪个芭蕾舞团女演员的身高更整齐?
解:甲团的平均身高= (163+164+164+165+165+165+166+167)≈165(cm),
乙团的平均身高= (163+164+164+165+166+167+167+168)≈166(cm),
所以S甲2= [(163﹣165)2+(164﹣165)2+(164﹣165)2+(165﹣165)2+(165﹣165)2+(165﹣165)2+(166﹣165)2+(167﹣165)2]≈1.38,
S乙2= [(163﹣166)2+(164﹣166)2+(164﹣166)2+(165﹣166)2+(166﹣166)2+(167﹣166)2+(167﹣166)2+(168﹣166)2]=3,
因为S甲2<S乙2,
所以甲芭蕾舞团女演员的身高更整齐.
1、计算下列各组数据的方差:
(1) 6 6 6 6 6 6 6;
(2) 5 5 6 6 6 7 7;
(3) 3 3 4 6 8 9 9;
(4) 3 3 3 6 9 9 9.
0
学以致用
2.某校从甲、乙两名优秀选手中选1名选手参加全市中学生射击比赛,近期的10次测试成绩得分情况如图所示.
(1)求甲、乙两名选手10次测试成绩的平均数和方差;
(2)请你运用所学过的统计知识做出判断,为了获得冠军,
派哪一位选手参加比赛更好?为什么?
(1)方差怎样计算?
(2)方差的适用条件:
当两组数据的平均数相等或相近时,才利用方差
来判断它们的波动情况.
(3)你如何理解方差的意义?
方差越大,数据的波动越大;
方差越小,数据的波动越小.
课堂小结
谢 谢
方差
课堂引入
在统计学中,除了平均数、中位数、众数这类刻画数据集中趋势的量以外,还有一类刻画数据波动程度的量,其中最重要的就是方差.
1.显示的是上海市2001年2月下旬和2002年同期的每日最高气温,如何对这两段气温进行比较呢?
探究1:方差
经计算可知这两个时段的平均气温相等,都是12℃,这是不是说,两个时段的气温情况总体上没有什么差异呢?
探究1:方差
观察下图,你感觉它们有没有差异呢?
通过观察,我们可以发现,图(A)中的点的波动范围比图(B)中的点波动范围要大.
图(A)中温度的最大值与最小值之间的差距很大,相差16℃,图(B)中温度的最大值与最小值相差7℃,由此,我们可以判定2001年同期气温波动范围要大.
2.小明和小兵两人参加体育项目训练,近期的5次测试成绩如表所示,谁的成绩较为稳定?为什么?
解:通过计算分析,两人测试成绩的平均数都是12.4,成绩的最大值与最小值也都相差4,但从下图中我们可以看到:相比下,小明的成绩大部分集中在平均数附近,而小兵的成绩与其平均数的离散程度略大.
通常,如果一组数据与其平均数的离散程度较小,我们就说它比较稳定.
那么,怎样的指标能反映一组数据与其平均数的离散程度呢?
统计学中常采用下面的做法来量化这组数据的波动大小:
设有n个数据x1,x2,…,xn,各数据与它们的平均
数 的差的平方分别是 ,
我们用这些值的平均数,即用
来衡量这组数据的波动大小,称它为这组数据的方差.
探究新知
方差越大,数据的波动越大;
方差越小,数据的波动越小.
探究新知
例1 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm),如表所示.
应用举例
甲 163 164 164 165 165 165 166 167
乙 163 164 164 165 166 167 167 168
哪个芭蕾舞团女演员的身高更整齐?
解:甲团的平均身高= (163+164+164+165+165+165+166+167)≈165(cm),
乙团的平均身高= (163+164+164+165+166+167+167+168)≈166(cm),
所以S甲2= [(163﹣165)2+(164﹣165)2+(164﹣165)2+(165﹣165)2+(165﹣165)2+(165﹣165)2+(166﹣165)2+(167﹣165)2]≈1.38,
S乙2= [(163﹣166)2+(164﹣166)2+(164﹣166)2+(165﹣166)2+(166﹣166)2+(167﹣166)2+(167﹣166)2+(168﹣166)2]=3,
因为S甲2<S乙2,
所以甲芭蕾舞团女演员的身高更整齐.
1、计算下列各组数据的方差:
(1) 6 6 6 6 6 6 6;
(2) 5 5 6 6 6 7 7;
(3) 3 3 4 6 8 9 9;
(4) 3 3 3 6 9 9 9.
0
学以致用
2.某校从甲、乙两名优秀选手中选1名选手参加全市中学生射击比赛,近期的10次测试成绩得分情况如图所示.
(1)求甲、乙两名选手10次测试成绩的平均数和方差;
(2)请你运用所学过的统计知识做出判断,为了获得冠军,
派哪一位选手参加比赛更好?为什么?
(1)方差怎样计算?
(2)方差的适用条件:
当两组数据的平均数相等或相近时,才利用方差
来判断它们的波动情况.
(3)你如何理解方差的意义?
方差越大,数据的波动越大;
方差越小,数据的波动越小.
课堂小结
谢 谢
