2021-2022学年度高一下数学必修第二册统计单元测试卷(Word含解析)
文档属性
| 名称 | 2021-2022学年度高一下数学必修第二册统计单元测试卷(Word含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 521.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 21:01:37 | ||
图片预览



文档简介
高一下数学必修第二册统计单元测试卷
第I卷(选择题)
一、单选题
1.有一组样本数据,由这组数据得到新样本数据,其中为非零常数,则( )
A.两组样本数据的样本平均数相同
B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差不相同
D.两组样数据的样本极差相同
2.某工厂利用随机数表对生产的600个零件进行抽样测试,先将600个零件进行编号001,002,…,599,600.从中抽取60个样本,根据提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的第6个样本编号是( )
33 21 18 34 29 78 64 56 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
A.457 B.328 C.253 D.072
3.甲 乙两人准备参加驾照科目一的考试,满分为100分,现统计了以往两人10次模拟考试的成绩,如下面茎叶图所示,则下列说法错误的是( )
A.甲成绩的中位数大于乙成绩的中位数 B.甲成绩的众数大于乙成绩的众数
C.甲成绩的极差大于乙成绩的极差 D.甲成绩的平均数小于乙成绩的平均数
4.为调查参加考试的高二级1200名学生的成绩情况,从中抽查了100名学生的成绩,就这个问题来说,下列说法正确的是( )
A.1200名学生是总体 B.每个学生是个体
C.样本容量是100 D.抽取的100名学生是样本
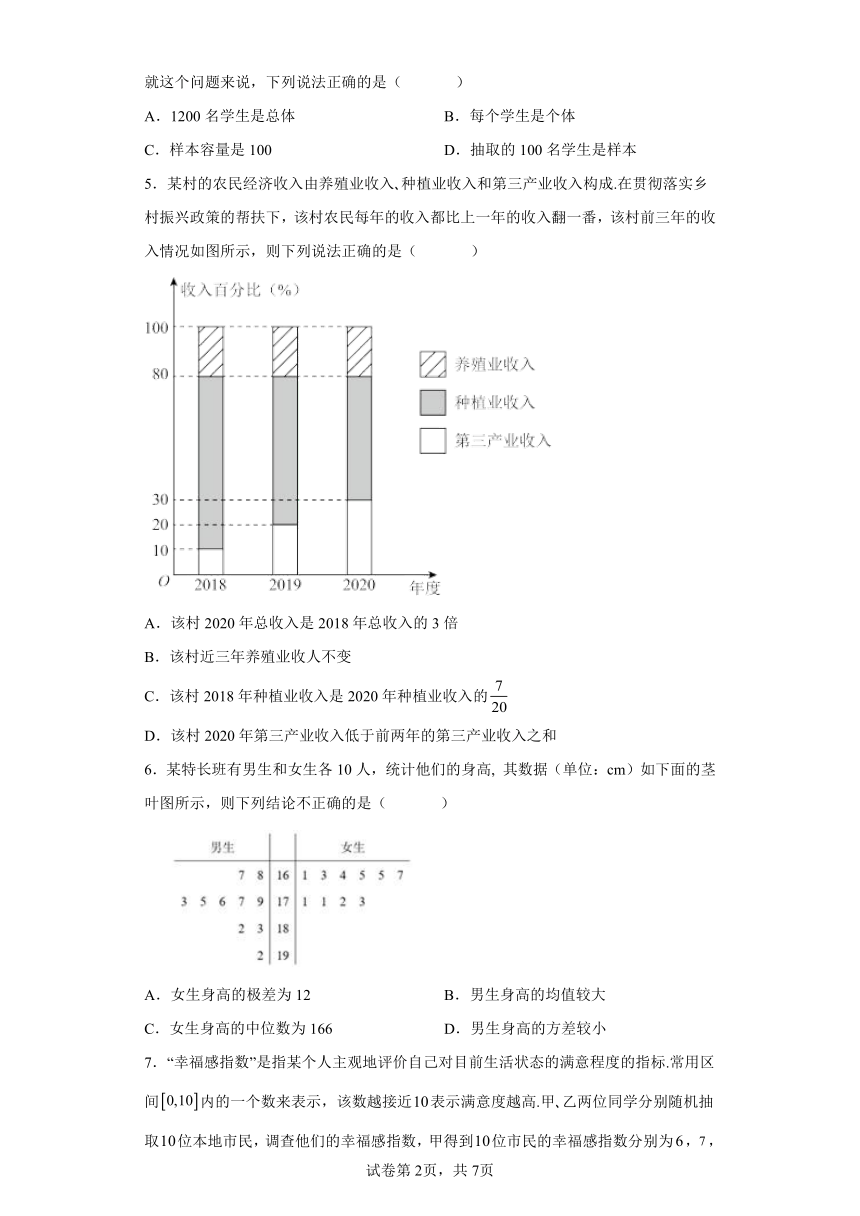
5.某村的农民经济收入由养殖业收入 种植业收入和第三产业收入构成.在贯彻落实乡村振兴政策的帮扶下,该村农民每年的收入都比上一年的收入翻一番,该村前三年的收入情况如图所示,则下列说法正确的是( )
A.该村2020年总收入是2018年总收入的3倍
B.该村近三年养殖业收人不变
C.该村2018年种植业收入是2020年种植业收入的
D.该村2020年第三产业收入低于前两年的第三产业收入之和
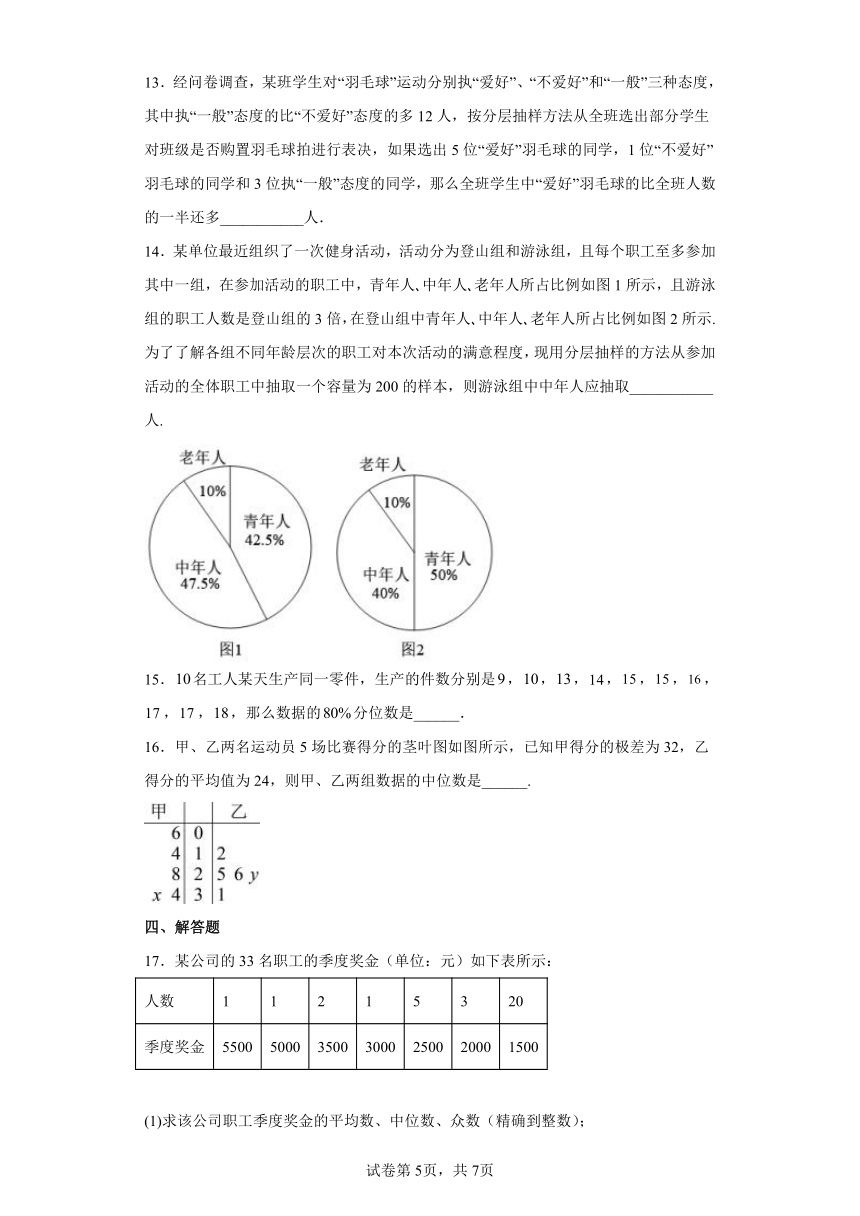
6.某特长班有男生和女生各10人,统计他们的身高, 其数据(单位:cm)如下面的茎叶图所示,则下列结论不正确的是( )
A.女生身高的极差为12 B.男生身高的均值较大
C.女生身高的中位数为166 D.男生身高的方差较小
7.“幸福感指数”是指某个人主观地评价自己对目前生活状态的满意程度的指标.常用区间内的一个数来表示,该数越接近表示满意度越高.甲 乙两位同学分别随机抽取位本地市民,调查他们的幸福感指数,甲得到位市民的幸福感指数分别为,,,,,,,,,,乙得到位市民的幸福感指数的平均数为,方差为,则这位市民幸福感指数的方差为( )
A. B. C. D.
8.下表为12名毕业生的起始月薪:
毕业生 1 2 3 4 5 6 7 8 9 10 11 12
起始月薪 2850 2950 3050 2880 2755 2710 2890 3130 2940 3325 2920 2880
根据表中所给的数据计算75%分位数为( )A.2950 B.3050 C.3130 D.3000
二、多选题
9.下表记录了某地区一年之内的月降水量
月份 1 2 3 4 5 6 7 8 9 10 11 12
月降水量/mm 58 48 53 46 56 56 51 71 56 53 64 66
对于上述表格中的数据,说法正确的是( )A.该年份月降水量的极差是25mm B.该年份月降水量的众数是53mm和56mm
C.该年份月降水量的25%分位数是52mm D.该年份月降水量的中位数是56mm
10.在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.过去10日,甲、乙、丙、丁四地新增疑似病例数据信息如下,则一定符合该标志的是( )
甲地:中位数为2,极差为5;
乙地:总体平均数为1,总体方差大于0;
丙地:总体平均数为2,众数为2;
丁地总体平均数为2,总体方差为3.
A.甲地 B.乙地
C.丙地 D.丁地
11.如图所示的两个扇形统计图分别统计了某地2010年和2020年小学生参加课外兴趣班的情况,已知2020年当地小学生参加课外兴趣班的总人数是2010年当地小学生参加课外兴趣班的总人数的4倍,则下列说法正确的是( )
A.2020年参加音乐兴趣班的小学生人数是2010年参加音乐兴趣班的小学生人数的4倍
B.这10年间,参加编程兴趣班的小学生人数变化最大
C.2020年参加美术兴趣班的小学生人数少于2010年参加美术兴趣班的小学生人数
D.相对于2010年,2020年参加不同课外兴趣班的小学生人数更平均
12.维生素又叫抗坏血酸,是一种水溶性维生素,是高等灵长类动物与其他少数生物的必需营养素,现从猕猴桃、柚子两种食物中测得每克维生素的含量(单位:),得到数据如下.则下列说法不正确的是( )
猕猴桃
柚子
A.每克柚子维生素含量的众数为
B.每克柚子维生素含量的分位数为
C.每克猕猴桃维生素含量的平均数高于每克柚子维生素含量的平均数
D.每克猕猴桃维生素含量的方差高于每克柚子维生素含量的方差
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.经问卷调查,某班学生对“羽毛球”运动分别执“爱好”、“不爱好”和“一般”三种态度,其中执“一般”态度的比“不爱好”态度的多12人,按分层抽样方法从全班选出部分学生对班级是否购置羽毛球拍进行表决,如果选出5位“爱好”羽毛球的同学,1位“不爱好”羽毛球的同学和3位执“一般”态度的同学,那么全班学生中“爱好”羽毛球的比全班人数的一半还多___________人.
14.某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加其中一组,在参加活动的职工中,青年人 中年人 老年人所占比例如图1所示,且游泳组的职工人数是登山组的3倍,在登山组中青年人 中年人 老年人所占比例如图2所示.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本,则游泳组中中年人应抽取___________人.
15.名工人某天生产同一零件,生产的件数分别是,,,,,,,,,,那么数据的分位数是______.
16.甲、乙两名运动员5场比赛得分的茎叶图如图所示,已知甲得分的极差为32,乙得分的平均值为24,则甲、乙两组数据的中位数是______.
四、解答题
17.某公司的33名职工的季度奖金(单位:元)如下表所示:
人数 1 1 2 1 5 3 20
季度奖金 5500 5000 3500 3000 2500 2000 1500
(1)求该公司职工季度奖金的平均数、中位数、众数(精确到整数);
(2)假设将表中的5000元提升到20000元,5500元提升到30000元,求新的平均数,中位数、众数(精确到整数);
(3)你认为哪个统计量更能反映该公司员工的季度奖金情况,结合此问题谈一谈你的看法.
18.为了解决下列问题,要收集什么数据?哪些问题需要应用样本?并就怎样选取样本说出自己的想法.
(1)要了解鱼塘中放养的鳞鱼的生长状况;
(2)某校想了解学生的视力状况.
19.某汽车租赁公司为了调查型汽车与型汽车的出租情况,现随机抽取这两种型号的汽车各辆,分别统计了每辆车在年月日至月日的出租天数,统计数据如下表:
型汽车
出租天数
车辆数
型汽车
出租天数 7
车辆数
(1)试根据上面的统计数据,判断这两种型号的汽车在年月日至月日出租天数的方差的大小关系;
(2)如果型汽车与型汽车每辆车每天出租获得的利润相同,该公司需要购买一辆汽车,请你根据所学的统计知识,给出建议应该购买哪一种车,并说明你的理由.
20.某射手在同一条件下射击30次,结果为:6环及6环以下2次,7环6次,8环7次,9环10次,10环5次.
(1)列出频率分布表;
(2)估计射手击中7~9环的可能性.
21.从某城市抽取100户居民进行月用电量调查,发现他们的用电量都在50到350度之间,将数据按照分成6组,画出的频率分布直方图如下图所示.
(1)求直方图中的值和月平均用电量的众数;
(2)已知该市有200万户居民,估计居民中用电量落在区间内的总户数,并说明理由.
22.已知某地连续10天的最低气温(单位:℃)依次是,,,,,和,,,,,若前5天的平均最低气温为7℃,求后5天的平均最低气温.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
利用平均数、中位数、标准差和极差的定义直接判断即可.
【详解】
解:样本数据,,,,新样本数据,,,,其中,为非零常数;
对于A,第一组数据的平均数为,则第二组数据的平均数为,平均数不同;
对于B,第一组数据的中位数是,则第二组数据的中位数是,中位数不同;
对于C,第一组数据的方差为,则第二组数据的方差也是,方差相同,所以标准差也相同;
对于D,第一组数据的极差为,第二组数据的样本极差是,极差相同.
故选:D.
2.D
【解析】
【分析】
由题设,根据随机数表读取前6个编号,注意编号大小不超过600且不可重复,即可知第6个样本编号.
【详解】
由题设,从第5行第6列开始向右读取数据,依次为253,313,457,860,736,253,007,328,623,457,889,072…
∵将600个零件进行编号001,002,…,599,600.
∴前6个编号分别为253,313,457,007,328,072.
∴第6个样本编号是072.
故选:D.
3.D
【解析】
【分析】
根据茎叶图求甲乙的中位数、众数、极差、平均数判断各选项的正误即可.
【详解】
由茎叶图知:甲成绩为,乙成绩为,
∴甲、乙的中位数分别为、,故A正确;
甲、乙的众数分别为、,故B正确;
甲、乙的极差分别为、,故C正确;
甲的平均数为,乙的平均数为,故D错误;
故选:D
4.C
【解析】
【分析】
根据总体、个体、样本容量、样本的定义,结合题意,即可判断和选择.
【详解】
根据题意,总体是名学生的成绩;个体是每个学生的成绩;
样本容量是,样本是抽取的100名学生的成绩;故正确的是C.
故选:C.
5.C
【解析】
【分析】
根据图表进行数据分析,对四个选项一一验证:
对于A:假设2018年的收入为a,计算出2020年的收入为,即可判断;
对于B:分别表示出近三年的养殖业收入,即可判断;
对于C:分别表示出2018年和2020年的种植业收入,即可判断;
对于D:分别求出2020年第三产业收入和前两年的第三产业收入之和即可判断
【详解】
对于A:假设2018年的收入为a,则2019年的收入为,2020年的收入为,该村2020年总收入是2018年总收入的4倍,故A错误;
对于B:近三年的养殖业收入分别为,故B错误;
对于C:2018年的种植业收入为,2020年的种植业收入为,故C正确;
对于D:该村2020年第三产业收入为,前两年的第三产业收入之和为,故D错误.
故选:C
6.D
【解析】
【分析】
对选项A,极差就是样本中的最大值减去最小值;对选项B,可直接计算出均值;对选项C,中位数就是按顺序排列的一组数据中居于中间位置的数;方差用来计算每一个变量(观察值)与总体均数之间的差异,根据茎叶图可以明显看出男生身高的方差较大.
【详解】
对选项A,女生身高的极差为173-161=12,故选项A正确;
对选项B,男生身高的均值为:
女生身高的均值为: ,故选项B正确;
对选项C,女生身高的中位数为 ,故选项C正确;
对选项D,根据茎叶图可以明显看出男生的身高更离散,而女生的身高更加集中,故男生身高的方差较大,故选项D错误;
故选:D
7.C
【解析】
【分析】
设乙得到位市民的幸福感指数为,甲得到位市民的幸福感指数为,求出,,由甲的方差可得的值,再求出的值,由方差公式即可求解.
【详解】
设乙得到位市民的幸福感指数为,则,
甲得到位市民的幸福感指数为,可得,,
所以这位市民的幸福感指数之和为,平均数为,
由方差的定义,乙所得数据的方差:,
由于,解得:.
因为甲得到位市民的幸福感指数为,,,,,,,,,,
所以,
所以这位市民的幸福感指数的方差为:
,
故选:C.
8.D
【解析】
【分析】
根据百分位数的定义计算即可.
【详解】
由小到大排列12个数据为2710,2757,2850,2880,2880,2890,2920,2940,2950,3050,3130,3325;
因为,
所以75%分位数为,
故选:D
9.ACD
【解析】
【分析】
A. 利用极差的定义判断;B.利用众数的定义判断;C.利用百分位数的定义判断;D.利用中位数的定义判断.
【详解】
A. 该年份月降水量的极差是71-46=25mm,故正确;
B.该年份月降水量的众数是56mm,故错误;
C.该年份月降水量从小到大为46,48,51,53,53,56,56,56,56,58,64,66,71,,
所以年份月降水量的25%分位数是,故正确;
D. 该年份月降水量从小到大为46,48,51,53,53,56,56,56,56,58,64,66,71,
所以该年份月降水量的中位数是,故正确;
故选:ACD
10.AD
【解析】
【分析】
对A,根据中位数和极差判断最大值是否超过7判断;对B,举例判断;对C,举例判断;对D,利用反证法,假设至少有一天疑似病例超过7人,不妨设8人,由方差大于判断.
【详解】
对A,因为甲地中位数为2,极差为5,故最大值不会大于.故A正确.
对B,若乙地过去10日分别为0,0,0,0,0,0,0,0,1,9,则满足总体平均数为1,总体方差大于0,但不满足每天新增疑似病例不超过7人,故B错误.
对C,若丙地过去10日分别为0,0,0,2,2,2,2,2,2,8,满足总体平均数为2,众数为2,但不满足每天新增疑似病例不超过7人,故C错误.
对D,假设至少有一天疑似病例超过7人,不妨设8人,则方差大于.与题设矛盾,故连续10天,每天新增疑似病例不超过7人.故D正确.
故选:AD.
11.ABD
【解析】
【分析】
设2010年参加课外兴趣班的小学生总人数为,则2020年参加课外兴趣班的小学生总人数是,根据扇形统计图中的比例计算,并逐项检验,即可得到结果.
【详解】
设2010年参加课外兴趣班的小学生总人数为,则2020年参加课外兴趣班的小学生总人数是;
由统计图可知,2010年参加音乐兴趣班的小学生人数是,
2020年参加音乐兴趣班的小学生人数是,故A正确.
这10年间参加编程兴趣班的小学生人数变化量为,
这10年间参加语言表演的小学生人数变化量为,
这10年间参加音乐的小学生人数变化量为,
这10年间参加美术的小学生人数变化量为,
所以这10年间参加编程兴趣班的小学生人数变化量最大,故B正确.
2020年参加美术兴趣班的小学生人数为,2010年参加美术兴趣班的小学生人数为,,故C不正确,
根据扇形统计图中的比例分布,可知D正确.
故选:ABD
12.BC
【解析】
【分析】
利用众数的概念可判断A选项;利用百分位数的定义可判断B选项;利用平均数公式可判断C选项;利用方差公式可判断D选项.
【详解】
对于A选项,每克柚子维生素含量的众数为,A对;
对于B选项,每克柚子维生素含量的分位数为,B错;
对于C选项,每克猕猴桃维生素含量的平均数为,
每克柚子维生素含量的平均数为,C错;
对于D选项,每克猕猴桃维生素含量的方差为
,
每克柚子维生素含量的方差为
,D对.
故选:BC.
13.3
【解析】
【分析】
根据分层抽样的比例设出各层人数,然后根据“一般”态度的比“不喜欢”态度的多12人求解出各层人数,由此可知“喜欢羽毛球”的人数以及全班人数,则结果可求.
【详解】
按分层抽样方法从全班选出部分学生对班级是否购置羽毛球拍进行表决,
5位“爱好”羽毛球的同学,1位“不爱好”羽毛球的同学和3位执“一般”态度的同学,
因为采用的是分层抽样且三类同学的人数比例为,
所以可设三类同学的人数分别为,
依题意,解得,
所以“喜欢”羽毛球的同学共有人,全班共有人,
所以人,
那么全班学生中“爱好”羽毛球的比全班人数的一半还多人.
故答案为:3.
14.75
【解析】
【分析】
题目考查分层抽样的方法,已知样本的总人数,所以,要求游泳组中中年人的人数,需要知道两个比例关系,一是游泳组占总人数的比例,题目已知为,二是游泳组中中年人的比例,这个需要结合以上两个图中总人数和登山人数的比例确定,确定之后,即可求出游泳组中中年人的数量
【详解】
设登山组的职工人数为,则游泳组的职工人数为,总人数为,所以容量为200的样本中,游泳组人数为150
根据图1可得:总人数中,老年人的人数为,同理,青年人的人数为 中年人的人数为;根据图2可得:登山组中,老年人的人数为,青年人的人数为,中年人的人数为,所以游泳组中,老年人的人数为,青年人的人数为,中年人的人数为,所以游泳组中,中年人占比为,所以游泳组中中年人的人数为人
故答案为:75
15.
【解析】
【分析】
根据百分位数的含义,计算即可得出数据的分位数.
【详解】
解:将名工人某天生产同一零件个数从小到大排列为,,,,,,,,,.因为,
所以样木数据的分位数为第个和第个数据的平均数,即.
故答案为:.
16.
【解析】
【分析】
先由极差以及平均数得出,进而得出中位数.
【详解】
由可得,,,因为乙得分的平均值为24,所以,所以甲、乙两组数据的中位数是.
故答案为:
17.(1)2091元,1500元, 1500元
(2)3288元,1500元, 1500元
(3)答案见解析
【解析】
【分析】
(1)利用求平均数的公式、中位数、众数的概念即求;
(2)利用求平均数的公式、中位数、众数的概念即求;
(3)结合实际及平均数、中位数、众数的含义可得.
(1)
平均数是
(元),
中位数是1500元,众数是1500元.
(2)
新的平均数是
(元),中位数是1500元,众数是1500元.
(3)
中位数或众数均能反映该公司员工的季度奖金情况.
因为公司中少数人的季度奖金与大多数人的季度奖金差别较大,导致平均数与中位数、众数偏差较大,所以平均数不能反映该公司员工的季度奖金情况.
18.(1)答案见解析
(2)答案见解析
【解析】
【分析】
(1)可判断要收集放养前后鱼的质量和健康状况,需要应用样本;
(2)要收集学生的视力数据,需要应用样本.
(1)
要了解鱼塘中放养的鳞鱼的生长状况,要收集放养前后鱼的质量和健康状况,需要应用样本,可分别从鱼塘的东、西、南、北、中五个方位捞起一定数量的鱼,分别测量其质量,并记录下健康状况,测量后的鱼再放回鱼塘,对测得的数据求平均数及标准差,结合健康状况作出结论.
(2)
要了解学生的视力状况,要收集学生的视力数据,需要应用样本,需要从不同的年级、不同性别的学生中抽取样本,分别测量视力后进行数据分析作出结论.
19.(1)型汽车在年月日至月日出租天数的方差较大;
(2)答案不唯一,理由见解析.
【解析】
【分析】
(1)根据方差的计算公式可直接求得结果;
(2)答案一:根据,可知型汽车的利润较大,则应该购买型汽车;
答案二:根据,可知型汽车的利润不稳定,则应该购买型汽车.
(1)
辆型汽车出租天数的平均数为;
.
辆型汽车出租天数的平均数为;
.
型汽车在年月日至月日出租天数的方差较大.
(2)
答案一:型汽车在年月日至月日出租天数的平均数为,型汽车在年月日至月日出租天数的平均数为,
选择型汽车的利润较大,故应该购买型汽车.
答案二:型汽车在年月日至月日出租天数的平均数为,型汽车在年月日至月日出租天数的平均数为,但型汽车出租天数的方差较大,利润不稳定.
应购买型汽车.
20.(1)频率分布表见解析.
(2)
【解析】
【分析】
(1)根据环数和次数列表即可.
(2)用击中7~9环的总次数除以30所得频率作为概率进行估计.
(1)
所中环数 7 8 9 10
击中次数 2 6 7 10 5
(2)
击中7~9环的总次数为6+7+10=23,频率为,
因此估计击中7~9环的可能性为.
21.(1),众数为度
(2)万户,理由见解析
【解析】
【分析】
(1)根据矩形面积之和为1可得x,由最高矩形底边中点横坐标估计众数;
(2)先求频率,再由总体频率可得.
(1)
根据频率和为1,可知,计算得.
由图可知,最高矩形的数据组为,所以众数为度.
(2)
由频率分布直方图知:用电量落在区间内的频率为
,
所以用电量落在区间内的总户数为万户.
22.10℃
【解析】
【分析】
根据前5天的平均最低气温为7℃可得,即可求出后5天的平均最低气温.
【详解】
因为前5天的平均最低气温为7℃,,则,
所以,
即后5天的平均最低气温为10℃.
答案第1页,共2页
答案第1页,共2页
第I卷(选择题)
一、单选题
1.有一组样本数据,由这组数据得到新样本数据,其中为非零常数,则( )
A.两组样本数据的样本平均数相同
B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差不相同
D.两组样数据的样本极差相同
2.某工厂利用随机数表对生产的600个零件进行抽样测试,先将600个零件进行编号001,002,…,599,600.从中抽取60个样本,根据提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的第6个样本编号是( )
33 21 18 34 29 78 64 56 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
A.457 B.328 C.253 D.072
3.甲 乙两人准备参加驾照科目一的考试,满分为100分,现统计了以往两人10次模拟考试的成绩,如下面茎叶图所示,则下列说法错误的是( )
A.甲成绩的中位数大于乙成绩的中位数 B.甲成绩的众数大于乙成绩的众数
C.甲成绩的极差大于乙成绩的极差 D.甲成绩的平均数小于乙成绩的平均数
4.为调查参加考试的高二级1200名学生的成绩情况,从中抽查了100名学生的成绩,就这个问题来说,下列说法正确的是( )
A.1200名学生是总体 B.每个学生是个体
C.样本容量是100 D.抽取的100名学生是样本
5.某村的农民经济收入由养殖业收入 种植业收入和第三产业收入构成.在贯彻落实乡村振兴政策的帮扶下,该村农民每年的收入都比上一年的收入翻一番,该村前三年的收入情况如图所示,则下列说法正确的是( )
A.该村2020年总收入是2018年总收入的3倍
B.该村近三年养殖业收人不变
C.该村2018年种植业收入是2020年种植业收入的
D.该村2020年第三产业收入低于前两年的第三产业收入之和
6.某特长班有男生和女生各10人,统计他们的身高, 其数据(单位:cm)如下面的茎叶图所示,则下列结论不正确的是( )
A.女生身高的极差为12 B.男生身高的均值较大
C.女生身高的中位数为166 D.男生身高的方差较小
7.“幸福感指数”是指某个人主观地评价自己对目前生活状态的满意程度的指标.常用区间内的一个数来表示,该数越接近表示满意度越高.甲 乙两位同学分别随机抽取位本地市民,调查他们的幸福感指数,甲得到位市民的幸福感指数分别为,,,,,,,,,,乙得到位市民的幸福感指数的平均数为,方差为,则这位市民幸福感指数的方差为( )
A. B. C. D.
8.下表为12名毕业生的起始月薪:
毕业生 1 2 3 4 5 6 7 8 9 10 11 12
起始月薪 2850 2950 3050 2880 2755 2710 2890 3130 2940 3325 2920 2880
根据表中所给的数据计算75%分位数为( )A.2950 B.3050 C.3130 D.3000
二、多选题
9.下表记录了某地区一年之内的月降水量
月份 1 2 3 4 5 6 7 8 9 10 11 12
月降水量/mm 58 48 53 46 56 56 51 71 56 53 64 66
对于上述表格中的数据,说法正确的是( )A.该年份月降水量的极差是25mm B.该年份月降水量的众数是53mm和56mm
C.该年份月降水量的25%分位数是52mm D.该年份月降水量的中位数是56mm
10.在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.过去10日,甲、乙、丙、丁四地新增疑似病例数据信息如下,则一定符合该标志的是( )
甲地:中位数为2,极差为5;
乙地:总体平均数为1,总体方差大于0;
丙地:总体平均数为2,众数为2;
丁地总体平均数为2,总体方差为3.
A.甲地 B.乙地
C.丙地 D.丁地
11.如图所示的两个扇形统计图分别统计了某地2010年和2020年小学生参加课外兴趣班的情况,已知2020年当地小学生参加课外兴趣班的总人数是2010年当地小学生参加课外兴趣班的总人数的4倍,则下列说法正确的是( )
A.2020年参加音乐兴趣班的小学生人数是2010年参加音乐兴趣班的小学生人数的4倍
B.这10年间,参加编程兴趣班的小学生人数变化最大
C.2020年参加美术兴趣班的小学生人数少于2010年参加美术兴趣班的小学生人数
D.相对于2010年,2020年参加不同课外兴趣班的小学生人数更平均
12.维生素又叫抗坏血酸,是一种水溶性维生素,是高等灵长类动物与其他少数生物的必需营养素,现从猕猴桃、柚子两种食物中测得每克维生素的含量(单位:),得到数据如下.则下列说法不正确的是( )
猕猴桃
柚子
A.每克柚子维生素含量的众数为
B.每克柚子维生素含量的分位数为
C.每克猕猴桃维生素含量的平均数高于每克柚子维生素含量的平均数
D.每克猕猴桃维生素含量的方差高于每克柚子维生素含量的方差
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.经问卷调查,某班学生对“羽毛球”运动分别执“爱好”、“不爱好”和“一般”三种态度,其中执“一般”态度的比“不爱好”态度的多12人,按分层抽样方法从全班选出部分学生对班级是否购置羽毛球拍进行表决,如果选出5位“爱好”羽毛球的同学,1位“不爱好”羽毛球的同学和3位执“一般”态度的同学,那么全班学生中“爱好”羽毛球的比全班人数的一半还多___________人.
14.某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加其中一组,在参加活动的职工中,青年人 中年人 老年人所占比例如图1所示,且游泳组的职工人数是登山组的3倍,在登山组中青年人 中年人 老年人所占比例如图2所示.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本,则游泳组中中年人应抽取___________人.
15.名工人某天生产同一零件,生产的件数分别是,,,,,,,,,,那么数据的分位数是______.
16.甲、乙两名运动员5场比赛得分的茎叶图如图所示,已知甲得分的极差为32,乙得分的平均值为24,则甲、乙两组数据的中位数是______.
四、解答题
17.某公司的33名职工的季度奖金(单位:元)如下表所示:
人数 1 1 2 1 5 3 20
季度奖金 5500 5000 3500 3000 2500 2000 1500
(1)求该公司职工季度奖金的平均数、中位数、众数(精确到整数);
(2)假设将表中的5000元提升到20000元,5500元提升到30000元,求新的平均数,中位数、众数(精确到整数);
(3)你认为哪个统计量更能反映该公司员工的季度奖金情况,结合此问题谈一谈你的看法.
18.为了解决下列问题,要收集什么数据?哪些问题需要应用样本?并就怎样选取样本说出自己的想法.
(1)要了解鱼塘中放养的鳞鱼的生长状况;
(2)某校想了解学生的视力状况.
19.某汽车租赁公司为了调查型汽车与型汽车的出租情况,现随机抽取这两种型号的汽车各辆,分别统计了每辆车在年月日至月日的出租天数,统计数据如下表:
型汽车
出租天数
车辆数
型汽车
出租天数 7
车辆数
(1)试根据上面的统计数据,判断这两种型号的汽车在年月日至月日出租天数的方差的大小关系;
(2)如果型汽车与型汽车每辆车每天出租获得的利润相同,该公司需要购买一辆汽车,请你根据所学的统计知识,给出建议应该购买哪一种车,并说明你的理由.
20.某射手在同一条件下射击30次,结果为:6环及6环以下2次,7环6次,8环7次,9环10次,10环5次.
(1)列出频率分布表;
(2)估计射手击中7~9环的可能性.
21.从某城市抽取100户居民进行月用电量调查,发现他们的用电量都在50到350度之间,将数据按照分成6组,画出的频率分布直方图如下图所示.
(1)求直方图中的值和月平均用电量的众数;
(2)已知该市有200万户居民,估计居民中用电量落在区间内的总户数,并说明理由.
22.已知某地连续10天的最低气温(单位:℃)依次是,,,,,和,,,,,若前5天的平均最低气温为7℃,求后5天的平均最低气温.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
利用平均数、中位数、标准差和极差的定义直接判断即可.
【详解】
解:样本数据,,,,新样本数据,,,,其中,为非零常数;
对于A,第一组数据的平均数为,则第二组数据的平均数为,平均数不同;
对于B,第一组数据的中位数是,则第二组数据的中位数是,中位数不同;
对于C,第一组数据的方差为,则第二组数据的方差也是,方差相同,所以标准差也相同;
对于D,第一组数据的极差为,第二组数据的样本极差是,极差相同.
故选:D.
2.D
【解析】
【分析】
由题设,根据随机数表读取前6个编号,注意编号大小不超过600且不可重复,即可知第6个样本编号.
【详解】
由题设,从第5行第6列开始向右读取数据,依次为253,313,457,860,736,253,007,328,623,457,889,072…
∵将600个零件进行编号001,002,…,599,600.
∴前6个编号分别为253,313,457,007,328,072.
∴第6个样本编号是072.
故选:D.
3.D
【解析】
【分析】
根据茎叶图求甲乙的中位数、众数、极差、平均数判断各选项的正误即可.
【详解】
由茎叶图知:甲成绩为,乙成绩为,
∴甲、乙的中位数分别为、,故A正确;
甲、乙的众数分别为、,故B正确;
甲、乙的极差分别为、,故C正确;
甲的平均数为,乙的平均数为,故D错误;
故选:D
4.C
【解析】
【分析】
根据总体、个体、样本容量、样本的定义,结合题意,即可判断和选择.
【详解】
根据题意,总体是名学生的成绩;个体是每个学生的成绩;
样本容量是,样本是抽取的100名学生的成绩;故正确的是C.
故选:C.
5.C
【解析】
【分析】
根据图表进行数据分析,对四个选项一一验证:
对于A:假设2018年的收入为a,计算出2020年的收入为,即可判断;
对于B:分别表示出近三年的养殖业收入,即可判断;
对于C:分别表示出2018年和2020年的种植业收入,即可判断;
对于D:分别求出2020年第三产业收入和前两年的第三产业收入之和即可判断
【详解】
对于A:假设2018年的收入为a,则2019年的收入为,2020年的收入为,该村2020年总收入是2018年总收入的4倍,故A错误;
对于B:近三年的养殖业收入分别为,故B错误;
对于C:2018年的种植业收入为,2020年的种植业收入为,故C正确;
对于D:该村2020年第三产业收入为,前两年的第三产业收入之和为,故D错误.
故选:C
6.D
【解析】
【分析】
对选项A,极差就是样本中的最大值减去最小值;对选项B,可直接计算出均值;对选项C,中位数就是按顺序排列的一组数据中居于中间位置的数;方差用来计算每一个变量(观察值)与总体均数之间的差异,根据茎叶图可以明显看出男生身高的方差较大.
【详解】
对选项A,女生身高的极差为173-161=12,故选项A正确;
对选项B,男生身高的均值为:
女生身高的均值为: ,故选项B正确;
对选项C,女生身高的中位数为 ,故选项C正确;
对选项D,根据茎叶图可以明显看出男生的身高更离散,而女生的身高更加集中,故男生身高的方差较大,故选项D错误;
故选:D
7.C
【解析】
【分析】
设乙得到位市民的幸福感指数为,甲得到位市民的幸福感指数为,求出,,由甲的方差可得的值,再求出的值,由方差公式即可求解.
【详解】
设乙得到位市民的幸福感指数为,则,
甲得到位市民的幸福感指数为,可得,,
所以这位市民的幸福感指数之和为,平均数为,
由方差的定义,乙所得数据的方差:,
由于,解得:.
因为甲得到位市民的幸福感指数为,,,,,,,,,,
所以,
所以这位市民的幸福感指数的方差为:
,
故选:C.
8.D
【解析】
【分析】
根据百分位数的定义计算即可.
【详解】
由小到大排列12个数据为2710,2757,2850,2880,2880,2890,2920,2940,2950,3050,3130,3325;
因为,
所以75%分位数为,
故选:D
9.ACD
【解析】
【分析】
A. 利用极差的定义判断;B.利用众数的定义判断;C.利用百分位数的定义判断;D.利用中位数的定义判断.
【详解】
A. 该年份月降水量的极差是71-46=25mm,故正确;
B.该年份月降水量的众数是56mm,故错误;
C.该年份月降水量从小到大为46,48,51,53,53,56,56,56,56,58,64,66,71,,
所以年份月降水量的25%分位数是,故正确;
D. 该年份月降水量从小到大为46,48,51,53,53,56,56,56,56,58,64,66,71,
所以该年份月降水量的中位数是,故正确;
故选:ACD
10.AD
【解析】
【分析】
对A,根据中位数和极差判断最大值是否超过7判断;对B,举例判断;对C,举例判断;对D,利用反证法,假设至少有一天疑似病例超过7人,不妨设8人,由方差大于判断.
【详解】
对A,因为甲地中位数为2,极差为5,故最大值不会大于.故A正确.
对B,若乙地过去10日分别为0,0,0,0,0,0,0,0,1,9,则满足总体平均数为1,总体方差大于0,但不满足每天新增疑似病例不超过7人,故B错误.
对C,若丙地过去10日分别为0,0,0,2,2,2,2,2,2,8,满足总体平均数为2,众数为2,但不满足每天新增疑似病例不超过7人,故C错误.
对D,假设至少有一天疑似病例超过7人,不妨设8人,则方差大于.与题设矛盾,故连续10天,每天新增疑似病例不超过7人.故D正确.
故选:AD.
11.ABD
【解析】
【分析】
设2010年参加课外兴趣班的小学生总人数为,则2020年参加课外兴趣班的小学生总人数是,根据扇形统计图中的比例计算,并逐项检验,即可得到结果.
【详解】
设2010年参加课外兴趣班的小学生总人数为,则2020年参加课外兴趣班的小学生总人数是;
由统计图可知,2010年参加音乐兴趣班的小学生人数是,
2020年参加音乐兴趣班的小学生人数是,故A正确.
这10年间参加编程兴趣班的小学生人数变化量为,
这10年间参加语言表演的小学生人数变化量为,
这10年间参加音乐的小学生人数变化量为,
这10年间参加美术的小学生人数变化量为,
所以这10年间参加编程兴趣班的小学生人数变化量最大,故B正确.
2020年参加美术兴趣班的小学生人数为,2010年参加美术兴趣班的小学生人数为,,故C不正确,
根据扇形统计图中的比例分布,可知D正确.
故选:ABD
12.BC
【解析】
【分析】
利用众数的概念可判断A选项;利用百分位数的定义可判断B选项;利用平均数公式可判断C选项;利用方差公式可判断D选项.
【详解】
对于A选项,每克柚子维生素含量的众数为,A对;
对于B选项,每克柚子维生素含量的分位数为,B错;
对于C选项,每克猕猴桃维生素含量的平均数为,
每克柚子维生素含量的平均数为,C错;
对于D选项,每克猕猴桃维生素含量的方差为
,
每克柚子维生素含量的方差为
,D对.
故选:BC.
13.3
【解析】
【分析】
根据分层抽样的比例设出各层人数,然后根据“一般”态度的比“不喜欢”态度的多12人求解出各层人数,由此可知“喜欢羽毛球”的人数以及全班人数,则结果可求.
【详解】
按分层抽样方法从全班选出部分学生对班级是否购置羽毛球拍进行表决,
5位“爱好”羽毛球的同学,1位“不爱好”羽毛球的同学和3位执“一般”态度的同学,
因为采用的是分层抽样且三类同学的人数比例为,
所以可设三类同学的人数分别为,
依题意,解得,
所以“喜欢”羽毛球的同学共有人,全班共有人,
所以人,
那么全班学生中“爱好”羽毛球的比全班人数的一半还多人.
故答案为:3.
14.75
【解析】
【分析】
题目考查分层抽样的方法,已知样本的总人数,所以,要求游泳组中中年人的人数,需要知道两个比例关系,一是游泳组占总人数的比例,题目已知为,二是游泳组中中年人的比例,这个需要结合以上两个图中总人数和登山人数的比例确定,确定之后,即可求出游泳组中中年人的数量
【详解】
设登山组的职工人数为,则游泳组的职工人数为,总人数为,所以容量为200的样本中,游泳组人数为150
根据图1可得:总人数中,老年人的人数为,同理,青年人的人数为 中年人的人数为;根据图2可得:登山组中,老年人的人数为,青年人的人数为,中年人的人数为,所以游泳组中,老年人的人数为,青年人的人数为,中年人的人数为,所以游泳组中,中年人占比为,所以游泳组中中年人的人数为人
故答案为:75
15.
【解析】
【分析】
根据百分位数的含义,计算即可得出数据的分位数.
【详解】
解:将名工人某天生产同一零件个数从小到大排列为,,,,,,,,,.因为,
所以样木数据的分位数为第个和第个数据的平均数,即.
故答案为:.
16.
【解析】
【分析】
先由极差以及平均数得出,进而得出中位数.
【详解】
由可得,,,因为乙得分的平均值为24,所以,所以甲、乙两组数据的中位数是.
故答案为:
17.(1)2091元,1500元, 1500元
(2)3288元,1500元, 1500元
(3)答案见解析
【解析】
【分析】
(1)利用求平均数的公式、中位数、众数的概念即求;
(2)利用求平均数的公式、中位数、众数的概念即求;
(3)结合实际及平均数、中位数、众数的含义可得.
(1)
平均数是
(元),
中位数是1500元,众数是1500元.
(2)
新的平均数是
(元),中位数是1500元,众数是1500元.
(3)
中位数或众数均能反映该公司员工的季度奖金情况.
因为公司中少数人的季度奖金与大多数人的季度奖金差别较大,导致平均数与中位数、众数偏差较大,所以平均数不能反映该公司员工的季度奖金情况.
18.(1)答案见解析
(2)答案见解析
【解析】
【分析】
(1)可判断要收集放养前后鱼的质量和健康状况,需要应用样本;
(2)要收集学生的视力数据,需要应用样本.
(1)
要了解鱼塘中放养的鳞鱼的生长状况,要收集放养前后鱼的质量和健康状况,需要应用样本,可分别从鱼塘的东、西、南、北、中五个方位捞起一定数量的鱼,分别测量其质量,并记录下健康状况,测量后的鱼再放回鱼塘,对测得的数据求平均数及标准差,结合健康状况作出结论.
(2)
要了解学生的视力状况,要收集学生的视力数据,需要应用样本,需要从不同的年级、不同性别的学生中抽取样本,分别测量视力后进行数据分析作出结论.
19.(1)型汽车在年月日至月日出租天数的方差较大;
(2)答案不唯一,理由见解析.
【解析】
【分析】
(1)根据方差的计算公式可直接求得结果;
(2)答案一:根据,可知型汽车的利润较大,则应该购买型汽车;
答案二:根据,可知型汽车的利润不稳定,则应该购买型汽车.
(1)
辆型汽车出租天数的平均数为;
.
辆型汽车出租天数的平均数为;
.
型汽车在年月日至月日出租天数的方差较大.
(2)
答案一:型汽车在年月日至月日出租天数的平均数为,型汽车在年月日至月日出租天数的平均数为,
选择型汽车的利润较大,故应该购买型汽车.
答案二:型汽车在年月日至月日出租天数的平均数为,型汽车在年月日至月日出租天数的平均数为,但型汽车出租天数的方差较大,利润不稳定.
应购买型汽车.
20.(1)频率分布表见解析.
(2)
【解析】
【分析】
(1)根据环数和次数列表即可.
(2)用击中7~9环的总次数除以30所得频率作为概率进行估计.
(1)
所中环数 7 8 9 10
击中次数 2 6 7 10 5
(2)
击中7~9环的总次数为6+7+10=23,频率为,
因此估计击中7~9环的可能性为.
21.(1),众数为度
(2)万户,理由见解析
【解析】
【分析】
(1)根据矩形面积之和为1可得x,由最高矩形底边中点横坐标估计众数;
(2)先求频率,再由总体频率可得.
(1)
根据频率和为1,可知,计算得.
由图可知,最高矩形的数据组为,所以众数为度.
(2)
由频率分布直方图知:用电量落在区间内的频率为
,
所以用电量落在区间内的总户数为万户.
22.10℃
【解析】
【分析】
根据前5天的平均最低气温为7℃可得,即可求出后5天的平均最低气温.
【详解】
因为前5天的平均最低气温为7℃,,则,
所以,
即后5天的平均最低气温为10℃.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
