2.6.2一元一次不等式组(2) 课件(共29张PPT)
文档属性
| 名称 | 2.6.2一元一次不等式组(2) 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 741.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
2.6.2一元一次不等式组(2)
第二章
一元一次不等式和一元一次不等式组
2021-2022学年八年级数学下册(北师大版)
学习目标
1.解较复杂的一元一次不等式组.
2.能根据具体问题中的数量关系,得出一元一次不等式组,解决简单的实际问题,并能根据实际问题的实际意义,检验结果是否符合题意
导入新课
设a<b 在数轴上表示解 解集
x>a
x>b
x<a
x<b
x>a
x<b
x<a
x>b
a
b
a
b
a
b
a
b
x>b
x<a
无解
a<x<b
大小小大中间找
大大小小无处找
同小取小
同大取大
规律(口诀)
1.完成下列表格
导入新课
先求出每个不等式的解集
①
再求各个解集的公共部分
②
确定该不等式组的解集
③
借助数轴
一元一次不等式组的解法:
讲授新课
较复杂的一元一次不等式组的解法
例1 :解不等式组:
解:解不等式①,得
x <-2.
解不等式②,得
x >3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
由图可以看出这两个不等式的解集没有公共部分.
所以,这个不等式组无解.
0
-2
3
讲授新课
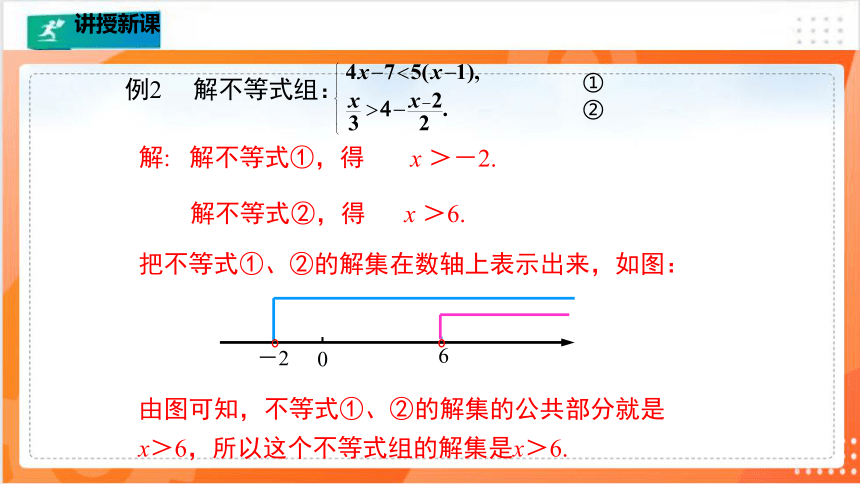
例2 解不等式组:
①
②
解: 解不等式①,得
x >-2.
解不等式②,得
x >6.
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是x>6.
讲授新课
例3 已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少
2x—a<1
x—2b>3
解: 由不等式组得:
x <
x >3+2b
因为不等式组的解集为: -1< x < 1 ,
所以,
=1
3a+2b= -1
解得
所以 (a+1)(b-1)=2×(-3)=-6.
b= -2
a= 1
讲授新课
一元一次不等式组的应用
例: 3个小组方案在10天内生产500件产品〔每天生产量相同〕,按原先的生产速度,不能完成任务;如果每个小组每天比原先生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
讲授新课
解:设每个小组原先每天生产x件产品,由题意,得
3×10x<500,
3×10(x+1)>500
解不等式组,得
根据题意,x的值应是整数,所以x=16.
答:每个小组原先每天生产16件产品.
列一元一次不等式组解实际问题的一般步骤:
〔1〕审题;
〔2〕设未知数,找不等量关系;
〔3〕根据不等关系列不等式组;
〔4〕解不等式组;
〔5〕检验并作答.
总结归纳
讲授新课
例:有假设干学生参加夏令营活动,晚上在一宾馆住宿时,如果每间住4个,那么还有20人住不下,相同的房间,如果每间住8人,那么还有一间住不满也不空,请问:这群学生有多少人?有多少房间供他们住?
讲授新课
解 设有x间房供他们住,那么学生有〔4x+20)人,
由题意,得
解不等式组,得5根据题意,x的值应是整数,所以x=6.
4x+20=44人.
答:有学生44人,有6间房供他们住.
(4x+20)-8(x-1)>0,
(4x+20)-8(x-1)<8.
讲授新课
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
例: 用假设干辆载重量为 8 t 的汽车运一批货物,假设每辆汽车只装 4 t ,那么剩下 20 t 货物;假设每辆汽车装满 8 t,那么最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x 辆汽车,那么这批货物共有〔4x+20 〕t.依题意得
解不等式组,得5<x <7.
讲授新课
分析已知量、未知量及它们之间的关系,找出题目中的不等关系.
审
设出合适的未知数.
设
根据题中的不等关系列出不等式组.
列
解不等式组,求出其解集.
解
检验所求出的不等式组的解集是否符合题意.
验
写出答案.
答
用一元一次不等式组解决实际问题的步骤
当堂检测
1. 不等式组 的最大整数解为( )
A.8 B.6 C.5 D.4
C
2. 如果代数式3x+2与代数式-2x+1的值都大于1,那么x的取值范围是( )
C
当堂检测
3.已知不等式组 有解,则a的取值范围为( )
A.a>-2 B.a≥-2 C.a<2 D.a≥2
C
4.把一些笔记本分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人就分不到3本,则共有学生人数为( )
A.6人 B.5人
C.6人或5人 D.4人
A
当堂检测
5. 在直角坐标系中,点(2x-6,x-5)在第四象限,则x的取值范围是 .
36.按图所示的程序进行操作,规定:程序运行从“输入一个值x”到“结果是否≥365”为一次操作.如果操作进行4次才能得到输出值,那么输入值x的取值范围是 .
5≤x<14
当堂检测
7. 已知关于x的不等式组 的解集为x<3,那么m的取值范围是________
m≥3
8.在方程组 中,若-3≤x-y<0,则k的取值范围是___________.
当堂检测
9. 解下列不等式组:
当堂检测
解:(1)解不等式①,得x>2.5.
解不等式②,得x≤4.
在数轴上表示不等式①和②的解集,如图,
这两个不等式解集的公共部分是2.5<x≤4.
所以不等式组的解集是2.5<x≤4.
当堂检测
(2)解不等式①,得x>2.
解不等式②,得x>4.
在数轴上表示不等式①和②的解集,如图.
这两个不等式解集的公共部分是x>4,
所以不等式组的解集是x>4.
当堂检测
(3)解不等式①,得x<-2.
解不等式②,得x>5.
在数轴上表示不等式①和②的解集,如图.
从数轴上可以看出,这两个不等式的解集没有公共部分,
所以这个不等式组无解.
当堂检测
因为不等式组的解集为: -1< x < 1 ,
所以 (a+1)(b-1)=2×(-3)=-6.
解: 由不等式组得:
10. 已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少
所以,
解得
当堂检测
11.我校八(2)班共有50名学生,老师安排每人制作一件A型或B型的陶艺品,学校现有甲种制作材料36 kg,乙种制作材料29 kg,制作A,B两种型号的陶艺品用料情况如表所示:
需甲种材料 需乙种材料
1件A型陶艺品 0.9 kg 0.3 kg
1件B型陶艺品 0.4 kg 1 kg
当堂检测
(1)设制作B型陶艺品x件,求x的取值范围.
(2)请你根据学校现有的材料,分别写出八(2)班制作A型和B型陶艺品的件数.
解:(1)由题意知:
解不等式组得:18≤x≤20.
(2)A型32件,B型18件;A型31件,B型19件;A型30件,B型20件.
当堂检测
解:(3)设获得的总利润为y元,
由题意知:y=10(50-x)+15x=5x+500 .
∵5>0,∴y随x的增大而增大.
则当x=20时,y最大值=600元.
故制作A型陶艺品30件,B型陶艺品20件时,
获得的利润最大为600元.
(3)若1件A型陶艺品和1件B型陶艺品销售获利分别为10元和15元,利用函数的性质,请分析说明如何制作获得的利润最大,最大利润为多少元
课堂小结
一元一次不等式组
利用公共部分确定不等式组的解集
分步解不等式
去括号、去分母
解较复杂的一元一次不等式组
→
实际应用(整数解)
→
https://www.21cnjy.com/help/help_extract.php
2.6.2一元一次不等式组(2)
第二章
一元一次不等式和一元一次不等式组
2021-2022学年八年级数学下册(北师大版)
学习目标
1.解较复杂的一元一次不等式组.
2.能根据具体问题中的数量关系,得出一元一次不等式组,解决简单的实际问题,并能根据实际问题的实际意义,检验结果是否符合题意
导入新课
设a<b 在数轴上表示解 解集
x>a
x>b
x<a
x<b
x>a
x<b
x<a
x>b
a
b
a
b
a
b
a
b
x>b
x<a
无解
a<x<b
大小小大中间找
大大小小无处找
同小取小
同大取大
规律(口诀)
1.完成下列表格
导入新课
先求出每个不等式的解集
①
再求各个解集的公共部分
②
确定该不等式组的解集
③
借助数轴
一元一次不等式组的解法:
讲授新课
较复杂的一元一次不等式组的解法
例1 :解不等式组:
解:解不等式①,得
x <-2.
解不等式②,得
x >3.
①
②
把不等式①、②的解集在数轴上表示出来,如图:
由图可以看出这两个不等式的解集没有公共部分.
所以,这个不等式组无解.
0
-2
3
讲授新课
例2 解不等式组:
①
②
解: 解不等式①,得
x >-2.
解不等式②,得
x >6.
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,所以这个不等式组的解集是x>6.
讲授新课
例3 已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少
2x—a<1
x—2b>3
解: 由不等式组得:
x <
x >3+2b
因为不等式组的解集为: -1< x < 1 ,
所以,
=1
3a+2b= -1
解得
所以 (a+1)(b-1)=2×(-3)=-6.
b= -2
a= 1
讲授新课
一元一次不等式组的应用
例: 3个小组方案在10天内生产500件产品〔每天生产量相同〕,按原先的生产速度,不能完成任务;如果每个小组每天比原先生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
讲授新课
解:设每个小组原先每天生产x件产品,由题意,得
3×10x<500,
3×10(x+1)>500
解不等式组,得
根据题意,x的值应是整数,所以x=16.
答:每个小组原先每天生产16件产品.
列一元一次不等式组解实际问题的一般步骤:
〔1〕审题;
〔2〕设未知数,找不等量关系;
〔3〕根据不等关系列不等式组;
〔4〕解不等式组;
〔5〕检验并作答.
总结归纳
讲授新课
例:有假设干学生参加夏令营活动,晚上在一宾馆住宿时,如果每间住4个,那么还有20人住不下,相同的房间,如果每间住8人,那么还有一间住不满也不空,请问:这群学生有多少人?有多少房间供他们住?
讲授新课
解 设有x间房供他们住,那么学生有〔4x+20)人,
由题意,得
解不等式组,得5
4x+20=44人.
答:有学生44人,有6间房供他们住.
(4x+20)-8(x-1)>0,
(4x+20)-8(x-1)<8.
讲授新课
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
例: 用假设干辆载重量为 8 t 的汽车运一批货物,假设每辆汽车只装 4 t ,那么剩下 20 t 货物;假设每辆汽车装满 8 t,那么最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x 辆汽车,那么这批货物共有〔4x+20 〕t.依题意得
解不等式组,得5<x <7.
讲授新课
分析已知量、未知量及它们之间的关系,找出题目中的不等关系.
审
设出合适的未知数.
设
根据题中的不等关系列出不等式组.
列
解不等式组,求出其解集.
解
检验所求出的不等式组的解集是否符合题意.
验
写出答案.
答
用一元一次不等式组解决实际问题的步骤
当堂检测
1. 不等式组 的最大整数解为( )
A.8 B.6 C.5 D.4
C
2. 如果代数式3x+2与代数式-2x+1的值都大于1,那么x的取值范围是( )
C
当堂检测
3.已知不等式组 有解,则a的取值范围为( )
A.a>-2 B.a≥-2 C.a<2 D.a≥2
C
4.把一些笔记本分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人就分不到3本,则共有学生人数为( )
A.6人 B.5人
C.6人或5人 D.4人
A
当堂检测
5. 在直角坐标系中,点(2x-6,x-5)在第四象限,则x的取值范围是 .
3
5≤x<14
当堂检测
7. 已知关于x的不等式组 的解集为x<3,那么m的取值范围是________
m≥3
8.在方程组 中,若-3≤x-y<0,则k的取值范围是___________.
9. 解下列不等式组:
当堂检测
解:(1)解不等式①,得x>2.5.
解不等式②,得x≤4.
在数轴上表示不等式①和②的解集,如图,
这两个不等式解集的公共部分是2.5<x≤4.
所以不等式组的解集是2.5<x≤4.
当堂检测
(2)解不等式①,得x>2.
解不等式②,得x>4.
在数轴上表示不等式①和②的解集,如图.
这两个不等式解集的公共部分是x>4,
所以不等式组的解集是x>4.
当堂检测
(3)解不等式①,得x<-2.
解不等式②,得x>5.
在数轴上表示不等式①和②的解集,如图.
从数轴上可以看出,这两个不等式的解集没有公共部分,
所以这个不等式组无解.
当堂检测
因为不等式组的解集为: -1< x < 1 ,
所以 (a+1)(b-1)=2×(-3)=-6.
解: 由不等式组得:
10. 已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少
所以,
解得
当堂检测
11.我校八(2)班共有50名学生,老师安排每人制作一件A型或B型的陶艺品,学校现有甲种制作材料36 kg,乙种制作材料29 kg,制作A,B两种型号的陶艺品用料情况如表所示:
需甲种材料 需乙种材料
1件A型陶艺品 0.9 kg 0.3 kg
1件B型陶艺品 0.4 kg 1 kg
当堂检测
(1)设制作B型陶艺品x件,求x的取值范围.
(2)请你根据学校现有的材料,分别写出八(2)班制作A型和B型陶艺品的件数.
解:(1)由题意知:
解不等式组得:18≤x≤20.
(2)A型32件,B型18件;A型31件,B型19件;A型30件,B型20件.
当堂检测
解:(3)设获得的总利润为y元,
由题意知:y=10(50-x)+15x=5x+500 .
∵5>0,∴y随x的增大而增大.
则当x=20时,y最大值=600元.
故制作A型陶艺品30件,B型陶艺品20件时,
获得的利润最大为600元.
(3)若1件A型陶艺品和1件B型陶艺品销售获利分别为10元和15元,利用函数的性质,请分析说明如何制作获得的利润最大,最大利润为多少元
课堂小结
一元一次不等式组
利用公共部分确定不等式组的解集
分步解不等式
去括号、去分母
解较复杂的一元一次不等式组
→
实际应用(整数解)
→
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
