2.4.1一元一次不等式(1) 课件(共28张PPT)
文档属性
| 名称 | 2.4.1一元一次不等式(1) 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 816.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 10:48:36 | ||
图片预览






文档简介
(共28张PPT)
2.4.1一元一次不等式(1)
第二章
一元一次不等式和一元一次不等式组
2021-2022学年八年级数学下册(北师大版)
学习目标
1.知道什么是一元一次不等式,会解简单的一元一次不等式并把解集表示在数轴上。
2.通过观察一元一次不等式的解法,对比解一元一次方程的步骤,归纳出解一元一次不等式的基本步骤。
导入新课
趣味阅读
有一次,鲁班的手不慎被一片小草叶子割破了,他发现小草叶子的边缘布满了密集的小齿,于是便产生联想,根据小草的结构发明了锯子.
鲁班在这里就运用了“类比”的思想方法,“类比”也是数学学习中常用的一种重要方法.
导入新课
等式的基本性质1:
等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式。
如果 ,那么 。
等式的基本性质2:
等式的两边都乘以(或除以)同一个不为0的数,所得的结果仍是等式。
如果 ,那么 或 。
不等式的基本性质1:
不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变。
如果 ,那么 。
不等式的基本性质2:
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
如果 ,且 那么 。
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变。
如果 ,且 那么 。
不等式的基本性质3:
导入新课
1、什么叫一元一次方程
答:只含一个未知数,并且未知数的最高次数是1 的方程.
2、一元一次方程 是一个等式,请问一元一次方程的(等号)两边都是怎样的式子
答:一元一次方程的(等号)两边都是整式.
5x=6, 4y=3-y, 2(11+x)=6
导入新课
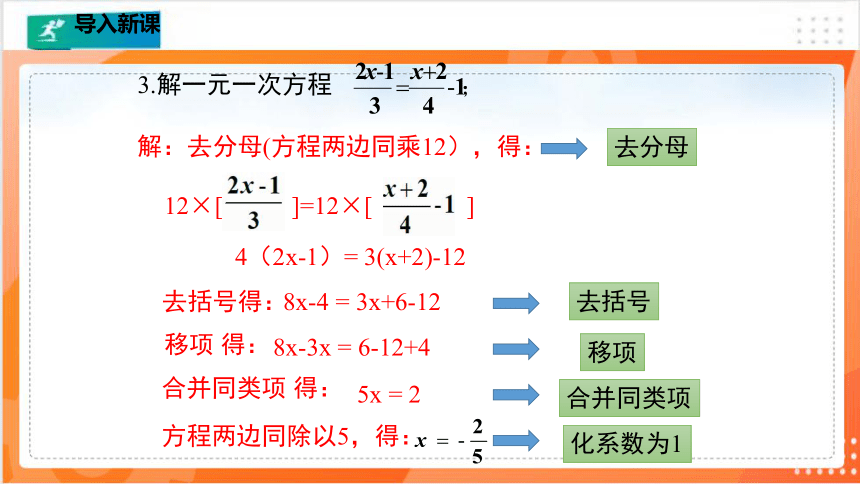
解:去分母(方程两边同乘12),得:
12×[ ]=12×[ ]
4(2x-1)= 3(x+2)-12
去括号得:
8x-4 = 3x+6-12
合并同类项 得:
5x = 2
方程两边同除以5,得:
去分母
去括号
移项 得:
8x-3x = 6-12+4
移项
合并同类项
化系数为1
3.解一元一次方程
导入新课
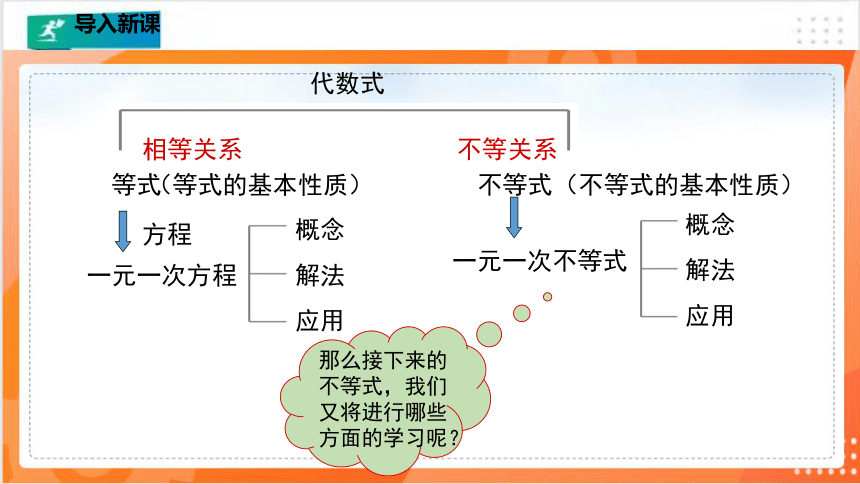
代数式
相等关系
不等关系
等式
不等式
一元一次方程
(等式的基本性质)
(不等式的基本性质)
一元一次不等式
应用
概念
解法
应用
概念
解法
方程
那么接下来的不等式,我们又将进行哪些方面的学习呢?
讲授新课
一元一次不等式的概念
观察下列不等式:
6+3x>30, x+17<5x, x>5 ,
这些不等式有哪些共同特点
一元一次不等式
1.只有一个未知数
2.未知数的指数是一次
3.不等号的两边都是整式
(1)含有几个未知数?
(2)未知数的最高次数是多少?
只含一个未知数,并且未知数的最高次数是1,不等式的左右两边都是整式,像这样的不等式,叫做一元一次不等式.
一元一次不等式的定义
(1)是用不等号连接的式子;
(2)两边都是整式;
(3)含有一个未知数;
(4)未知数最高次数为1且其系数不为0.
一元一次不等式必须同时满足的“四个条件”:
概括总结
讲授新课
例1 下列式子中是一元一次不等式的有( )
(1)x2+1>2x; (2) +2>0;
(3)x>y; (4) ≤1.
A.1个 B.2个 C.3个 D.4个
A
分析:(1)中未知数的最高次数是2,故不是一元一次不等式;
(2)中左边不是整式,故不是一元一次不等式;
(3)中有两个未知数,故不是一元一次不等式;
(4)是一元一次不等式.
讲授新课
解一元一次不等式
解不等式:
4x-1<5x+15
解方程:
4x-1=5x+15
解:移项,得
4x-5x=15+1
合并同类项,得
-x=16
系数化为1,得
x=-16
解:移项,得
4x-5x<15+1
合并同类项,得
-x<16
系数化为1,得
x>-16
归纳总结
解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式;而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为xa的形式.
讲授新课
解一元一次不等式的过程和解一元一次方程有什么关系?
一元一次方程 一元一次不等式
解法步骤
区别
解的情况
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
若乘(或除以)负数,要把不等号方向改变
一般解集含有无数个解
若乘(或除以)负数,等号不变
一般只有一个解
讲授新课
例2 解不等式3-x<2x+6,并把它的解集表示在数轴上.
解:方程两边都加-2x ,得3-x -2x <2x+6-2x .
合并同类项,得3-3x <6 .
两边都加-3,得3-3x-3 <6 -3 .
合并同类项,得-3x <3 .
两边都除以-3,得x>-1.
这个不等式的解集在数轴上的表示如图所示:
4
-4
-2
0
2
1
3
-3
-1
讲授新课
解:去分母,得3(x -2) ≥2(7-x) .
去括号,得3x- 6≥14-2x .
移项、合并同类项,得5x ≥20 .
两边都除以5,得x≥4.
这个不等式的解集在数轴上的表示如图所示:
例3 解不等式 ,并把它的解集表示在数轴上.
7
-1
1
3
5
4
6
0
2
讲授新课
解一元一次不等式的步骤:
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)化系数为1
不要漏乘常数项,分子是多项式是要加括号
移项要变号
乘或除以同一个负数时,不等号的方向要改变.
括号前是“-”号时,去括号要变号
讲授新课
解一元一次不等式的注意事项:
(2)要注意区分“大于”、“不大于”、“小于”、“不小于”等数学语言的使用,并把这些表示不等关系的语言用数学符号准确的表达出来.
(3)在数轴上表示解集应注意的问题:
方向、空心或实心.
(1)在运用性质3时要特别注意:
不等式两边都乘以或除以同一个负数时,要改变不等号的方向.
当堂检测
1. 下列不等式中,是一元一次不等式的是( )
B.a2+b2>0
C. >1 D.x<y
A
2.不等式2x-3>-5的解集在数轴上表示正确的是 ( )
C
当堂检测
3. 解不等式 ≥x-1,下列去分母正确的是( )
A.2x+1-3x-1≥x-1
B.2(x+1)-3(x-1)≥x-1
C.2x+1-3x-1≥6x-1
D.2(x+1)-3(x-1)≥6(x-1)
D
当堂检测
4. 解不等式 的过程中,开始出现错误的一步是( )
①去分母,得5(x+2)>3(2x-1);
②去括号,得5x+10>6x-3;
③移项、合并同类项,得-x>-13;
④系数化为1,得x>13.
A.① B.② C.③ D.④
D
当堂检测
5.若(m-2)x2m+1-1>5是关于x的一元一次不等式,
则m=______.
0
0,1,2
6. 当自然数k=_________时,关于x的方程 x-3k=5(x-k)+6的解是负数.
当堂检测
7. 解下列不等式,并把它们的解集分别表示在数轴上:
(1)5x>-10; (2)-3x+12≤0;
(3) (4)
解:(1)两边都除以5,得x>-2.
这个不等式的解集在数轴上的表示如图所示:
4
-4
-2
0
2
1
3
-3
-1
当堂检测
(2)移项、合并同类项,得-3x ≤ - 12 .
两边都除以-3,得x≥4.
这个不等式的解集在数轴上的表示如图所示:
7
-1
1
3
5
4
6
0
2
(3)去分母,得3(x -1)<2(4x-5) .
去括号,得3x-3 < 8x-10.
移项、合并同类项,得-5x < - 7 .
两边都除以-5,得x> .
这个不等式的解集在数轴上的表示如图所示:
7
-1
1
3
5
4
6
0
2
当堂检测
(4)去分母,得(x +7) -2<3x+2 .
去括号,得x+7- 2 < 3x+2 .
移项、合并同类项,得-2x < - 3 .
两边都除以-2,得x> .
这个不等式的解集在数轴上的表示如图所示:
7
-1
1
3
5
4
6
0
2
当堂检测
8、解不等式 ≥ -2,并把它的解集表示在数轴上.
解:去分母,得3(2+x)≥2(2x-1)-12,
去括号,得6+3x≥4x-2-12,
移项,得3x-4x≥-2-12-6,
合并同类项,得-x≥-20,
系数化为1,得x≤20.
0
10
20
课堂小结
一元一次不等式的概念和
解法
一元一次不等式的概念
解一元一次不等式的步骤
只含一个未知数,并且未知数的最高次数是1,不等式的左右两边都是整式,像这样的不等式,叫做一元一次不等式.
去分母 去括号 移项
合并同类项 不等式
两边同除以未知数的系数.
https://www.21cnjy.com/help/help_extract.php
2.4.1一元一次不等式(1)
第二章
一元一次不等式和一元一次不等式组
2021-2022学年八年级数学下册(北师大版)
学习目标
1.知道什么是一元一次不等式,会解简单的一元一次不等式并把解集表示在数轴上。
2.通过观察一元一次不等式的解法,对比解一元一次方程的步骤,归纳出解一元一次不等式的基本步骤。
导入新课
趣味阅读
有一次,鲁班的手不慎被一片小草叶子割破了,他发现小草叶子的边缘布满了密集的小齿,于是便产生联想,根据小草的结构发明了锯子.
鲁班在这里就运用了“类比”的思想方法,“类比”也是数学学习中常用的一种重要方法.
导入新课
等式的基本性质1:
等式的两边都加上(或减去)同一个数或同一个整式,所得的结果仍是等式。
如果 ,那么 。
等式的基本性质2:
等式的两边都乘以(或除以)同一个不为0的数,所得的结果仍是等式。
如果 ,那么 或 。
不等式的基本性质1:
不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变。
如果 ,那么 。
不等式的基本性质2:
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
如果 ,且 那么 。
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变。
如果 ,且 那么 。
不等式的基本性质3:
导入新课
1、什么叫一元一次方程
答:只含一个未知数,并且未知数的最高次数是1 的方程.
2、一元一次方程 是一个等式,请问一元一次方程的(等号)两边都是怎样的式子
答:一元一次方程的(等号)两边都是整式.
5x=6, 4y=3-y, 2(11+x)=6
导入新课
解:去分母(方程两边同乘12),得:
12×[ ]=12×[ ]
4(2x-1)= 3(x+2)-12
去括号得:
8x-4 = 3x+6-12
合并同类项 得:
5x = 2
方程两边同除以5,得:
去分母
去括号
移项 得:
8x-3x = 6-12+4
移项
合并同类项
化系数为1
3.解一元一次方程
导入新课
代数式
相等关系
不等关系
等式
不等式
一元一次方程
(等式的基本性质)
(不等式的基本性质)
一元一次不等式
应用
概念
解法
应用
概念
解法
方程
那么接下来的不等式,我们又将进行哪些方面的学习呢?
讲授新课
一元一次不等式的概念
观察下列不等式:
6+3x>30, x+17<5x, x>5 ,
这些不等式有哪些共同特点
一元一次不等式
1.只有一个未知数
2.未知数的指数是一次
3.不等号的两边都是整式
(1)含有几个未知数?
(2)未知数的最高次数是多少?
只含一个未知数,并且未知数的最高次数是1,不等式的左右两边都是整式,像这样的不等式,叫做一元一次不等式.
一元一次不等式的定义
(1)是用不等号连接的式子;
(2)两边都是整式;
(3)含有一个未知数;
(4)未知数最高次数为1且其系数不为0.
一元一次不等式必须同时满足的“四个条件”:
概括总结
讲授新课
例1 下列式子中是一元一次不等式的有( )
(1)x2+1>2x; (2) +2>0;
(3)x>y; (4) ≤1.
A.1个 B.2个 C.3个 D.4个
A
分析:(1)中未知数的最高次数是2,故不是一元一次不等式;
(2)中左边不是整式,故不是一元一次不等式;
(3)中有两个未知数,故不是一元一次不等式;
(4)是一元一次不等式.
讲授新课
解一元一次不等式
解不等式:
4x-1<5x+15
解方程:
4x-1=5x+15
解:移项,得
4x-5x=15+1
合并同类项,得
-x=16
系数化为1,得
x=-16
解:移项,得
4x-5x<15+1
合并同类项,得
-x<16
系数化为1,得
x>-16
归纳总结
解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式;而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为x
讲授新课
解一元一次不等式的过程和解一元一次方程有什么关系?
一元一次方程 一元一次不等式
解法步骤
区别
解的情况
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
若乘(或除以)负数,要把不等号方向改变
一般解集含有无数个解
若乘(或除以)负数,等号不变
一般只有一个解
讲授新课
例2 解不等式3-x<2x+6,并把它的解集表示在数轴上.
解:方程两边都加-2x ,得3-x -2x <2x+6-2x .
合并同类项,得3-3x <6 .
两边都加-3,得3-3x-3 <6 -3 .
合并同类项,得-3x <3 .
两边都除以-3,得x>-1.
这个不等式的解集在数轴上的表示如图所示:
4
-4
-2
0
2
1
3
-3
-1
讲授新课
解:去分母,得3(x -2) ≥2(7-x) .
去括号,得3x- 6≥14-2x .
移项、合并同类项,得5x ≥20 .
两边都除以5,得x≥4.
这个不等式的解集在数轴上的表示如图所示:
例3 解不等式 ,并把它的解集表示在数轴上.
7
-1
1
3
5
4
6
0
2
讲授新课
解一元一次不等式的步骤:
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)化系数为1
不要漏乘常数项,分子是多项式是要加括号
移项要变号
乘或除以同一个负数时,不等号的方向要改变.
括号前是“-”号时,去括号要变号
讲授新课
解一元一次不等式的注意事项:
(2)要注意区分“大于”、“不大于”、“小于”、“不小于”等数学语言的使用,并把这些表示不等关系的语言用数学符号准确的表达出来.
(3)在数轴上表示解集应注意的问题:
方向、空心或实心.
(1)在运用性质3时要特别注意:
不等式两边都乘以或除以同一个负数时,要改变不等号的方向.
当堂检测
1. 下列不等式中,是一元一次不等式的是( )
B.a2+b2>0
C. >1 D.x<y
A
2.不等式2x-3>-5的解集在数轴上表示正确的是 ( )
C
当堂检测
3. 解不等式 ≥x-1,下列去分母正确的是( )
A.2x+1-3x-1≥x-1
B.2(x+1)-3(x-1)≥x-1
C.2x+1-3x-1≥6x-1
D.2(x+1)-3(x-1)≥6(x-1)
D
当堂检测
4. 解不等式 的过程中,开始出现错误的一步是( )
①去分母,得5(x+2)>3(2x-1);
②去括号,得5x+10>6x-3;
③移项、合并同类项,得-x>-13;
④系数化为1,得x>13.
A.① B.② C.③ D.④
D
当堂检测
5.若(m-2)x2m+1-1>5是关于x的一元一次不等式,
则m=______.
0
0,1,2
6. 当自然数k=_________时,关于x的方程 x-3k=5(x-k)+6的解是负数.
当堂检测
7. 解下列不等式,并把它们的解集分别表示在数轴上:
(1)5x>-10; (2)-3x+12≤0;
(3) (4)
解:(1)两边都除以5,得x>-2.
这个不等式的解集在数轴上的表示如图所示:
4
-4
-2
0
2
1
3
-3
-1
当堂检测
(2)移项、合并同类项,得-3x ≤ - 12 .
两边都除以-3,得x≥4.
这个不等式的解集在数轴上的表示如图所示:
7
-1
1
3
5
4
6
0
2
(3)去分母,得3(x -1)<2(4x-5) .
去括号,得3x-3 < 8x-10.
移项、合并同类项,得-5x < - 7 .
两边都除以-5,得x> .
这个不等式的解集在数轴上的表示如图所示:
7
-1
1
3
5
4
6
0
2
当堂检测
(4)去分母,得(x +7) -2<3x+2 .
去括号,得x+7- 2 < 3x+2 .
移项、合并同类项,得-2x < - 3 .
两边都除以-2,得x> .
这个不等式的解集在数轴上的表示如图所示:
7
-1
1
3
5
4
6
0
2
当堂检测
8、解不等式 ≥ -2,并把它的解集表示在数轴上.
解:去分母,得3(2+x)≥2(2x-1)-12,
去括号,得6+3x≥4x-2-12,
移项,得3x-4x≥-2-12-6,
合并同类项,得-x≥-20,
系数化为1,得x≤20.
0
10
20
课堂小结
一元一次不等式的概念和
解法
一元一次不等式的概念
解一元一次不等式的步骤
只含一个未知数,并且未知数的最高次数是1,不等式的左右两边都是整式,像这样的不等式,叫做一元一次不等式.
去分母 去括号 移项
合并同类项 不等式
两边同除以未知数的系数.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
