3.1用表格表示的变量间关系 课件(共29张PPT)
文档属性
| 名称 | 3.1用表格表示的变量间关系 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 11:03:02 | ||
图片预览






文档简介
(共29张PPT)
北师大版 七年级下册数学
第三章 变量之间的关系
3.1用表格表示的变量间关系
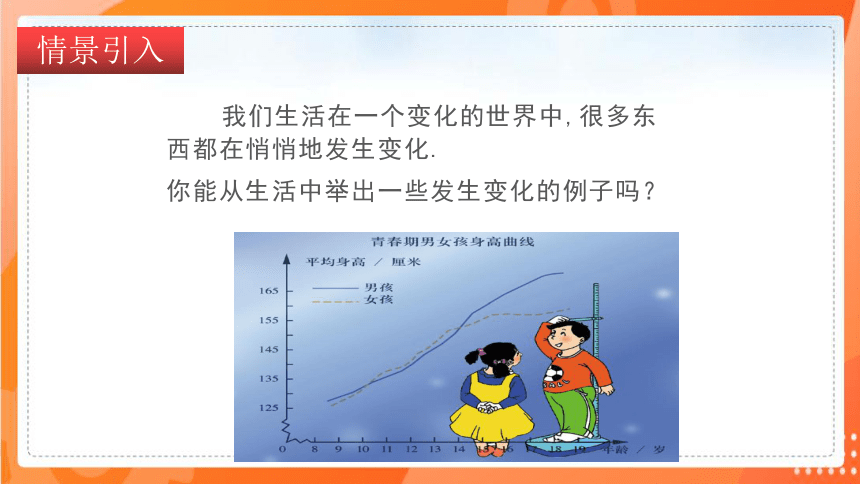
我们生活在一个变化的世界中,很多东西都在悄悄地发生变化.
你能从生活中举出一些发生变化的例子吗?
情景引入
气温随海拔而变化
自主探究
1.婴儿
6个月、1周岁、2周岁时体重分别大约是出生时的2倍、
3倍、4倍,
6周岁、10周岁时体重分别约是1周岁时的2倍、3倍.
一、变量与函数
年龄 刚出生 6个月 1周岁 2周岁 6周岁 10周岁
体重 /千克
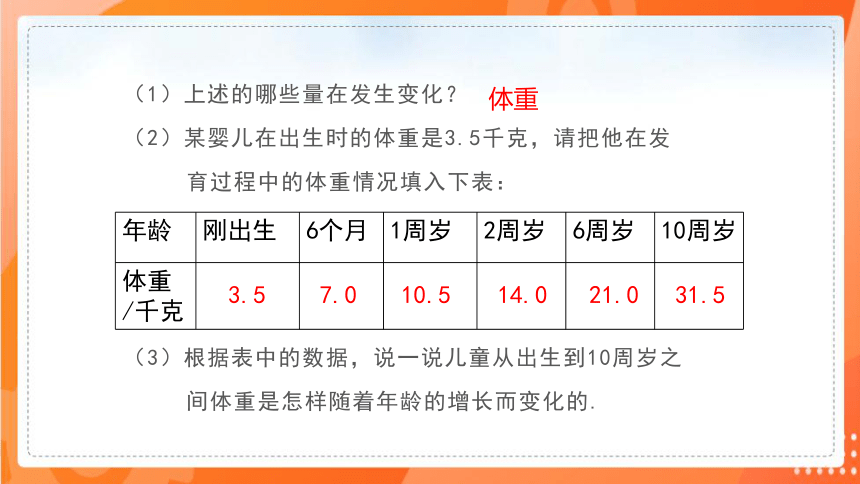
(1)上述的哪些量在发生变化?
(2)某婴儿在出生时的体重是3.5千克,请把他在发
育过程中的体重情况填入下表:
(3)根据表中的数据,说一说儿童从出生到10周岁之
间体重是怎样随着年龄的增长而变化的.
3.5
7.0
10.5
14.0
21.0
31.5
体重
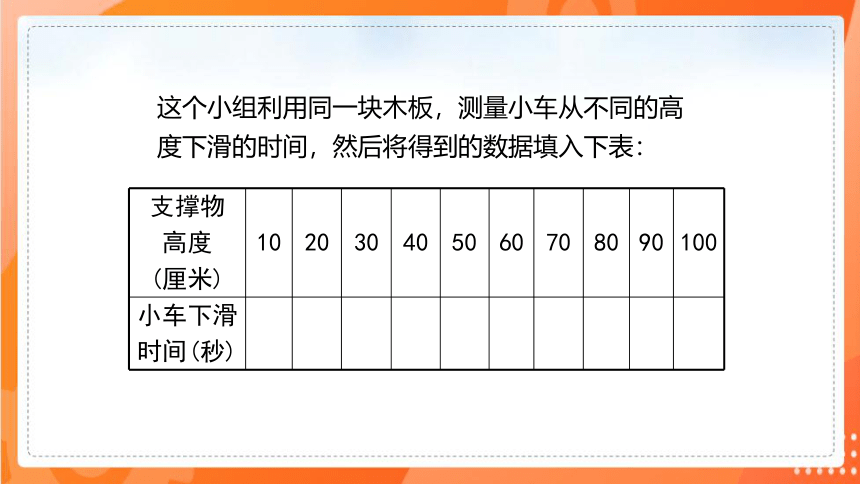
2.王波学习小组做了一个实验:小车下滑的时间.
这个小组利用同一块木板,测量小车从不同的高度下滑的时间,然后将得到的数据填入下表:
支撑物 高度 (厘米) 10 20 30 40 50 60 70 80 90 100
小车下滑 时间(秒)
细心体会哦!
20
0
40
60
80
100
单位:cm
下面是王波学习小组得到的数据:
10 20 30 40 50 60 70 80 90 100
(1)支撑物高度为70厘米时,小车下滑时间
是多少?1.59秒
4.23
1.35
1.41
1.50
1.59
1.71
1.89
2.13
2.45
3.00
根据上表回答下列问题:
支撑物高度
/厘米
小车下滑时间/秒
h
t
演示
1.23
0.55
0.32
0.24
0.18
0.12
0.09
0.09
0.06
(3)h每增加10厘米,t的变化情况相同吗?
(4)估计当h=110厘米时,t的值是多少,你是怎
样估计的?
(2)如果用h表示支撑物高度,t表示小车下滑时
间,随着h逐渐变大,t的变化趋势是什么?
变小
不同
(5)随着支撑物高度h的变化,还有哪些量发生
变化?哪些量始终不发生变化?
估计是1.30秒,因为时间越来越少.
时间发生了变化,木板的长度没变化.
在“小车下滑的时间”中,支撑物的高度h和小车下滑的时间t都在变化,它们都是变量(variable).其中小车下滑的时间t随支撑物的高度h的变化而变化.支撑物的高度h是自变量(independent variale),小车下滑的时间t是因变量(dependent variale).
在这一变化过程中,小车下滑的距离(木板的长度)一直没有变化.像这种在变化过程中数值始终不变的量叫作常量(constant).
归纳总结
我国从1949年到1999年的人口统计数据如下:(精确到0.01亿):
时间/年x 1949 1959 1969 1979 1989 1999
人口/亿y 5.42 6.72 8.07 9.75 11.07 12.59
1.30
1.35
1.68
1.32
1.52
议一议
(2)x和y哪个是自变量 哪个是因变量
(1)如果用x表示时间,y表示我国人口总数,那么
随着x的变化,y的变化趋势是什么?
(3)从1949年起,时间每向后推移10年,我国人口
是怎样变化的?
(4)你能根据此表格预测2009年时我国人口将会是
多少?
议一议
增大
x是自变量,y是因变量.
越来越多
超过13亿
例题1、研究表明,当钾肥和磷肥的施用量一定时,土豆的产量与氮肥的施用量有如下关系:
氮肥施用量 千克/公顷 0 34 67 101 135 202 259 336 404 471
土豆产量 吨/公顷 15.18 21.36 25.72 32.29 34.03 39.45 43.15 43.46 40.83 30.75
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
解:氮肥施用量和土豆产量之间的关系;
氮肥施用量是自变量,土豆产量是因变量。
二、用表格表示变量间关系
例题分析
(2)当氮肥的施用量是101千克/公顷时,土豆的产量是多少?如果不施氮肥呢?
(3)根据表格中的数据,你认为氮肥的施用量是多少时比较适宜?说说你的理由。
解:32.29 t / hm , 15.18 t / hm
解:氮肥施用量为336kg/hm2时比较适宜,因为此时土豆的产量最高。
树苗的生长情况表:
(1)从小树苗长成参天大树的过程中哪些量发生了变化?其中,自变量和因变量分别是哪个变量?
年数(年) 0 1 2 3 4 5 ...
树高(米) 1.5 1.7 1.9 2.1 2.3 2.5 ...
解:由表中数据知:变量分别是年数和树高。
自变量:年数
因变量:树高
例题2
(2)请你根据以上信息预测第 六 年、第 八年树的高度以及当小树苗长到3.5米时,所需的年数。
解:第六 年时:2.5 + 0.2 = 2.7(米)
第 八年时:2.7 + 0.2 + 0.2 = 3.1(米)
自变量:x(年);因变量:y(米)
y = 0.2 x + 1.5
小树苗长到 3.5 米时:3.5 = 0.2 x + 1.5
x =10
年数(年) 0 1 2 3 4 5 ...
树高(米) 1.5 1.7 1.9 2.1 2.3 2.5 ...
例题3.父亲告诉小明:“距离地面越远,温度越低”,并且出示了下面的表格:
据表,父亲还给小明出了下面几个问题,请你和小明一起回答:
(1)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t如何变化?(降低)
(2)你知道距离地面5千米的高空温度是多少吗?( -10 ℃ )
(3)你能预测距离地面6千米的高空温度是多少吗( -16(℃). )
【规律总结】
用表格表示变量之间关系的“三个一”
一个优点:根据表格中已列出的自变量的值,可以直接查到与其对应的因变量的值,使用起来比较方便.
一个不足:表格中所列出的对应值一般都是有限的,由表格不容易看出两个变量之间的对应规律,不能直观、形象地反映变量之间的变化趋势.
一个注意:用表格表示变量之间关系时,要先表示自变量,再表示因变量,在表示自变量和因变量时,第一列要写单位名称.
1.骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化.在这一问题中,自变量是( )
(A)沙漠 (B)体温 (C)时间 (D)骆驼
【解析】因为骆驼的体温随时间的变化而变化,所以自变量是时间.
C
课堂练习
2.对于圆的周长公式C=2πR,下列说法正确的是( )
(A)π,R是变量,2是常量
(B)R是变量,π是常量
(C)C是变量,π,R是常量
(D)C,R是变量,2,π是常量
【解析】因为常量就是在变化过程中不变的量,变量是指在变化过程中发生变化的量.所以C,R是变量,2,π是常量.
D
【变式备选】在△ABC中,它的底边是a,底边上的高是h,则三
角形面积S= ah,当a为定长时,在此式中( )
(A)S,h是变量, ,a是常量
(B)S,h,a是变量, 是常量
(C)S,h是变量, ,a是常量
(D)S是变量, ,a,h是常量
【解析】因为三角形面积S= ah,所以当a为定长时,在此
式中S,h是变量, ,a是常量.
A
3.婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,以上叙述中,______________发生变化,自变量是________,因变量是________.
【解析】因为婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,所以年龄和体重发生变化,自变量是年龄,因变量是体重.
年龄和体重
年龄
体重
4.某布行购进了一批花布,销售的数量与销售收入之间的关系如下:
(1)如果用x表示花布的销售数量,y表示花布的销售收入,随着x的逐渐变大,y的变化趋势是____________.
(2)在这个变化过程中,自变量是________,因变量是________.
(3)当花布销售数量由2米变到6米时,花布销售收入由_____元变到_____元.
【解析】随着销售数量x的逐渐变大,销售收入y逐渐变大.自变量是销售数量,因变量是销售收入.当销售数量是2米时,销售收入是16.6元,当销售数量是6米时,销售收入是49.8元.
逐渐变大
销售数量
销售收入
16.6 49.8
5.下表所列为某商店薄利多销的情况.某商品原价为560元,随着不同幅度的降价,日销量(单位为件)发生相应的变化(如表):
这个表反映了____个变量之间的关系,______是自变量,________是因变量.从表中可以看出每降价5元,日销量增加____件,从而可以估计降价之前的日销量为____件.
【解析】表中反映了两个变量之间的关系,因为日销量随降价的改变而改变,所以降价是自变量,日销量是因变量.从表中可以看出每降价5元,日销量增加30件,所以可以估计降价之前的日销量为780-30=750(件).
两
降价
日销量
30
750
6.某河受暴雨袭击,某天此河水的水位记录如下表:
(1)上表反映了哪两个变量之间的关系?
(2)12时的水位是多高?
(3)哪一时段水位上升最快?
解: (1)由表可知:反映了时间和水位之间的关系.
(2)由表可以看出:12时的水位是4米.
(3)由表可以看出:在相等的时间间隔内,20时至24时水位上升最快.
1. 掌握自变量和因变量的概念。
2.用表格表示变量间的关系.
通过本课时的学习,需要我们掌握:
课堂小结
https://www.21cnjy.com/help/help_extract.php
北师大版 七年级下册数学
第三章 变量之间的关系
3.1用表格表示的变量间关系
我们生活在一个变化的世界中,很多东西都在悄悄地发生变化.
你能从生活中举出一些发生变化的例子吗?
情景引入
气温随海拔而变化
自主探究
1.婴儿
6个月、1周岁、2周岁时体重分别大约是出生时的2倍、
3倍、4倍,
6周岁、10周岁时体重分别约是1周岁时的2倍、3倍.
一、变量与函数
年龄 刚出生 6个月 1周岁 2周岁 6周岁 10周岁
体重 /千克
(1)上述的哪些量在发生变化?
(2)某婴儿在出生时的体重是3.5千克,请把他在发
育过程中的体重情况填入下表:
(3)根据表中的数据,说一说儿童从出生到10周岁之
间体重是怎样随着年龄的增长而变化的.
3.5
7.0
10.5
14.0
21.0
31.5
体重
2.王波学习小组做了一个实验:小车下滑的时间.
这个小组利用同一块木板,测量小车从不同的高度下滑的时间,然后将得到的数据填入下表:
支撑物 高度 (厘米) 10 20 30 40 50 60 70 80 90 100
小车下滑 时间(秒)
细心体会哦!
20
0
40
60
80
100
单位:cm
下面是王波学习小组得到的数据:
10 20 30 40 50 60 70 80 90 100
(1)支撑物高度为70厘米时,小车下滑时间
是多少?1.59秒
4.23
1.35
1.41
1.50
1.59
1.71
1.89
2.13
2.45
3.00
根据上表回答下列问题:
支撑物高度
/厘米
小车下滑时间/秒
h
t
演示
1.23
0.55
0.32
0.24
0.18
0.12
0.09
0.09
0.06
(3)h每增加10厘米,t的变化情况相同吗?
(4)估计当h=110厘米时,t的值是多少,你是怎
样估计的?
(2)如果用h表示支撑物高度,t表示小车下滑时
间,随着h逐渐变大,t的变化趋势是什么?
变小
不同
(5)随着支撑物高度h的变化,还有哪些量发生
变化?哪些量始终不发生变化?
估计是1.30秒,因为时间越来越少.
时间发生了变化,木板的长度没变化.
在“小车下滑的时间”中,支撑物的高度h和小车下滑的时间t都在变化,它们都是变量(variable).其中小车下滑的时间t随支撑物的高度h的变化而变化.支撑物的高度h是自变量(independent variale),小车下滑的时间t是因变量(dependent variale).
在这一变化过程中,小车下滑的距离(木板的长度)一直没有变化.像这种在变化过程中数值始终不变的量叫作常量(constant).
归纳总结
我国从1949年到1999年的人口统计数据如下:(精确到0.01亿):
时间/年x 1949 1959 1969 1979 1989 1999
人口/亿y 5.42 6.72 8.07 9.75 11.07 12.59
1.30
1.35
1.68
1.32
1.52
议一议
(2)x和y哪个是自变量 哪个是因变量
(1)如果用x表示时间,y表示我国人口总数,那么
随着x的变化,y的变化趋势是什么?
(3)从1949年起,时间每向后推移10年,我国人口
是怎样变化的?
(4)你能根据此表格预测2009年时我国人口将会是
多少?
议一议
增大
x是自变量,y是因变量.
越来越多
超过13亿
例题1、研究表明,当钾肥和磷肥的施用量一定时,土豆的产量与氮肥的施用量有如下关系:
氮肥施用量 千克/公顷 0 34 67 101 135 202 259 336 404 471
土豆产量 吨/公顷 15.18 21.36 25.72 32.29 34.03 39.45 43.15 43.46 40.83 30.75
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
解:氮肥施用量和土豆产量之间的关系;
氮肥施用量是自变量,土豆产量是因变量。
二、用表格表示变量间关系
例题分析
(2)当氮肥的施用量是101千克/公顷时,土豆的产量是多少?如果不施氮肥呢?
(3)根据表格中的数据,你认为氮肥的施用量是多少时比较适宜?说说你的理由。
解:32.29 t / hm , 15.18 t / hm
解:氮肥施用量为336kg/hm2时比较适宜,因为此时土豆的产量最高。
树苗的生长情况表:
(1)从小树苗长成参天大树的过程中哪些量发生了变化?其中,自变量和因变量分别是哪个变量?
年数(年) 0 1 2 3 4 5 ...
树高(米) 1.5 1.7 1.9 2.1 2.3 2.5 ...
解:由表中数据知:变量分别是年数和树高。
自变量:年数
因变量:树高
例题2
(2)请你根据以上信息预测第 六 年、第 八年树的高度以及当小树苗长到3.5米时,所需的年数。
解:第六 年时:2.5 + 0.2 = 2.7(米)
第 八年时:2.7 + 0.2 + 0.2 = 3.1(米)
自变量:x(年);因变量:y(米)
y = 0.2 x + 1.5
小树苗长到 3.5 米时:3.5 = 0.2 x + 1.5
x =10
年数(年) 0 1 2 3 4 5 ...
树高(米) 1.5 1.7 1.9 2.1 2.3 2.5 ...
例题3.父亲告诉小明:“距离地面越远,温度越低”,并且出示了下面的表格:
据表,父亲还给小明出了下面几个问题,请你和小明一起回答:
(1)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t如何变化?(降低)
(2)你知道距离地面5千米的高空温度是多少吗?( -10 ℃ )
(3)你能预测距离地面6千米的高空温度是多少吗( -16(℃). )
【规律总结】
用表格表示变量之间关系的“三个一”
一个优点:根据表格中已列出的自变量的值,可以直接查到与其对应的因变量的值,使用起来比较方便.
一个不足:表格中所列出的对应值一般都是有限的,由表格不容易看出两个变量之间的对应规律,不能直观、形象地反映变量之间的变化趋势.
一个注意:用表格表示变量之间关系时,要先表示自变量,再表示因变量,在表示自变量和因变量时,第一列要写单位名称.
1.骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化.在这一问题中,自变量是( )
(A)沙漠 (B)体温 (C)时间 (D)骆驼
【解析】因为骆驼的体温随时间的变化而变化,所以自变量是时间.
C
课堂练习
2.对于圆的周长公式C=2πR,下列说法正确的是( )
(A)π,R是变量,2是常量
(B)R是变量,π是常量
(C)C是变量,π,R是常量
(D)C,R是变量,2,π是常量
【解析】因为常量就是在变化过程中不变的量,变量是指在变化过程中发生变化的量.所以C,R是变量,2,π是常量.
D
【变式备选】在△ABC中,它的底边是a,底边上的高是h,则三
角形面积S= ah,当a为定长时,在此式中( )
(A)S,h是变量, ,a是常量
(B)S,h,a是变量, 是常量
(C)S,h是变量, ,a是常量
(D)S是变量, ,a,h是常量
【解析】因为三角形面积S= ah,所以当a为定长时,在此
式中S,h是变量, ,a是常量.
A
3.婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,以上叙述中,______________发生变化,自变量是________,因变量是________.
【解析】因为婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,所以年龄和体重发生变化,自变量是年龄,因变量是体重.
年龄和体重
年龄
体重
4.某布行购进了一批花布,销售的数量与销售收入之间的关系如下:
(1)如果用x表示花布的销售数量,y表示花布的销售收入,随着x的逐渐变大,y的变化趋势是____________.
(2)在这个变化过程中,自变量是________,因变量是________.
(3)当花布销售数量由2米变到6米时,花布销售收入由_____元变到_____元.
【解析】随着销售数量x的逐渐变大,销售收入y逐渐变大.自变量是销售数量,因变量是销售收入.当销售数量是2米时,销售收入是16.6元,当销售数量是6米时,销售收入是49.8元.
逐渐变大
销售数量
销售收入
16.6 49.8
5.下表所列为某商店薄利多销的情况.某商品原价为560元,随着不同幅度的降价,日销量(单位为件)发生相应的变化(如表):
这个表反映了____个变量之间的关系,______是自变量,________是因变量.从表中可以看出每降价5元,日销量增加____件,从而可以估计降价之前的日销量为____件.
【解析】表中反映了两个变量之间的关系,因为日销量随降价的改变而改变,所以降价是自变量,日销量是因变量.从表中可以看出每降价5元,日销量增加30件,所以可以估计降价之前的日销量为780-30=750(件).
两
降价
日销量
30
750
6.某河受暴雨袭击,某天此河水的水位记录如下表:
(1)上表反映了哪两个变量之间的关系?
(2)12时的水位是多高?
(3)哪一时段水位上升最快?
解: (1)由表可知:反映了时间和水位之间的关系.
(2)由表可以看出:12时的水位是4米.
(3)由表可以看出:在相等的时间间隔内,20时至24时水位上升最快.
1. 掌握自变量和因变量的概念。
2.用表格表示变量间的关系.
通过本课时的学习,需要我们掌握:
课堂小结
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
