3.1图形的平移 课件(共37张PPT)
文档属性
| 名称 | 3.1图形的平移 课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 11:05:38 | ||
图片预览





文档简介
(共37张PPT)
北师大版八年级下册数学
第三章 图形的平移与旋转
3.1 图形的平移
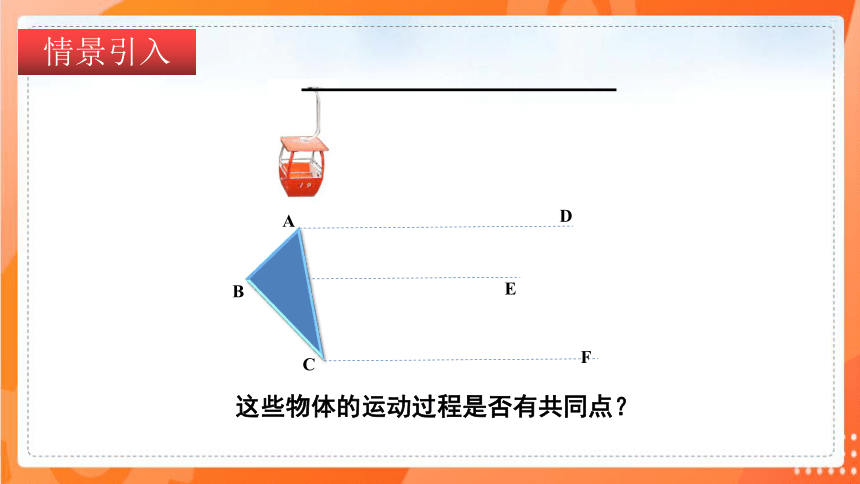
这些物体的运动过程是否有共同点?
A
B
C
D
E
F
情景引入
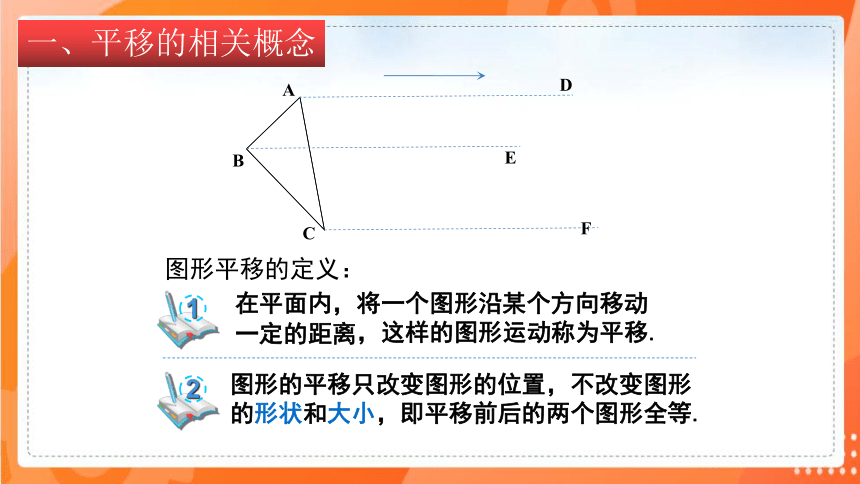
在平面内,将一个图形沿 移动一定的距离,这样的图形运动称为平移.
图形平移的定义:
1
A
B
C
D
E
F
某个方向
一定的距离
图形的平移只改变图形的位置,不改变图形的形状和大小,即平移前后的两个图形全等.
2
一、平移的相关概念
说说你生活中见过的图形的平移例子
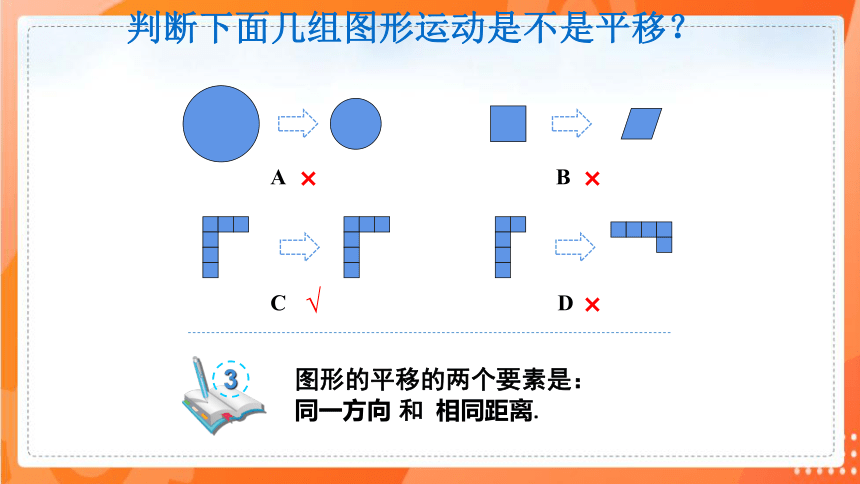
图形的平移的两个要素是:
同一方向 和 相同距离.
判断下面几组图形运动是不是平移?
3
A
C
D
B
×
×
√
×
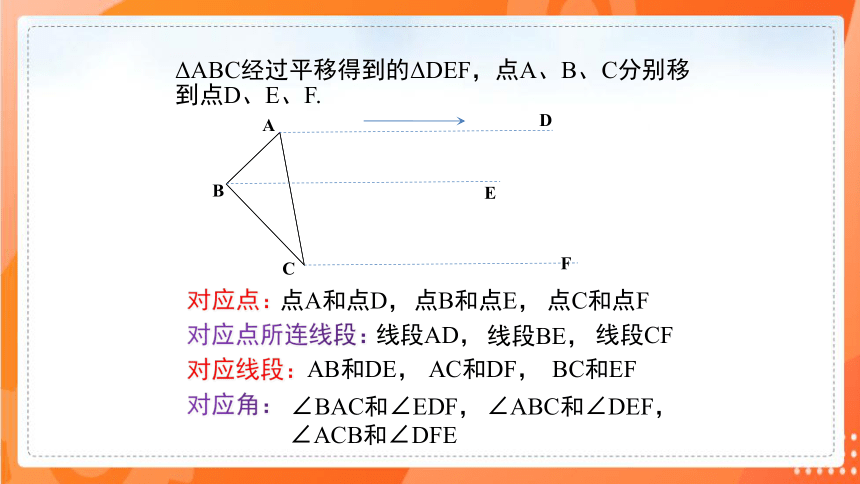
ΔABC经过平移得到的ΔDEF,点A、B、C分别移到点D、E、F.
对应角:
对应点所连线段:
对应线段:
AB和DE,
AC和DF,
BC和EF
∠BAC和∠EDF,
∠ABC和∠DEF,
∠ACB和∠DFE
线段AD,
线段BE,
线段CF
对应点:
点A和点D,
点B和点E,
点C和点F
A
B
C
D
E
F
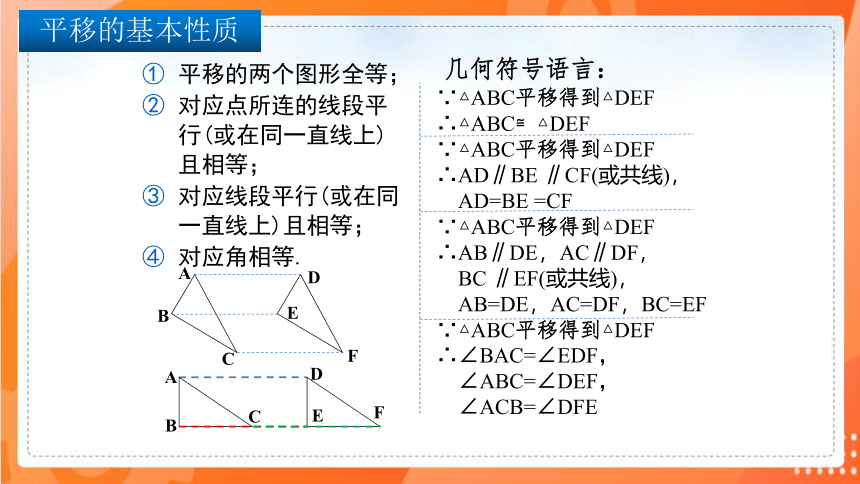
几何符号语言:
平移的两个图形全等;
对应点所连的线段平行(或在同一直线上)且相等;
对应线段平行(或在同一直线上)且相等;
对应角相等.
A
B
C
D
E
F
A
B
C
D
E
F
∵△ABC平移得到△DEF
∴△ABC≌△DEF
∵△ABC平移得到△DEF
∴AD∥BE ∥CF(或共线),
AD=BE =CF
∵△ABC平移得到△DEF
∴AB∥DE,AC∥DF,
BC ∥EF(或共线),
AB=DE,AC=DF,BC=EF
∵△ABC平移得到△DEF
∴∠BAC=∠EDF,
∠ABC=∠DEF,
∠ACB=∠DFE
平移的基本性质
如图,在ΔABC中,∠C=90°,∠ABC=30°,AB=4,将ΔABC沿射线PQ的方向平移5个单位长度后得到ΔA′B′C′,则
A
C
B
A′
C′
B′
P
Q
A′C′的长为 ;
∠B′A′C′的度数为 ;
四边形ABB′A′的周长为 .
2
60 °
18
练一练
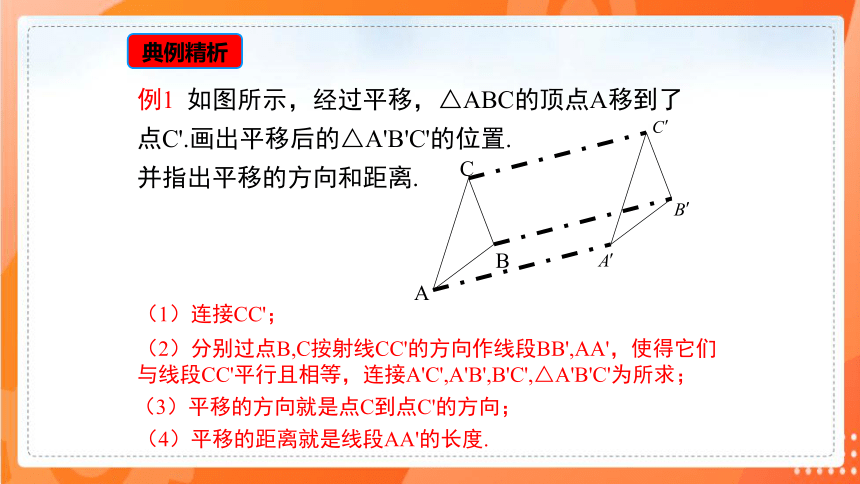
例1 如图所示,经过平移,△ABC的顶点A移到了点C'.画出平移后的△A'B'C'的位置.
并指出平移的方向和距离.
A
B
C
(1)连接CC';
(2)分别过点B,C按射线CC'的方向作线段BB',AA',使得它们与线段CC'平行且相等,连接A'C',A'B',B'C',△A'B'C'为所求;
(3)平移的方向就是点C到点C'的方向;
(4)平移的距离就是线段AA'的长度.
典例精析
B
C
A
例2:如图,经过平移,ΔABC的顶点A移到了点D,作出平移后的三角形.
E
F
D
解:如图,连接AD,过B、C点分别做线段BE、CF使得他们与线段AD平行且相等,连接 DE、DF、EF,ΔDEF就是ΔABC平移后的图形.
B
C
A
想一想:有其他的方法吗?
E
F
D
解:如图,过点D按射线AB的方向做线段DE平行且等于AB;过点D按射线AC的方向做线段DF平行且等于AC;连接EF. ΔDEF 就是ΔABC平移后的图形.
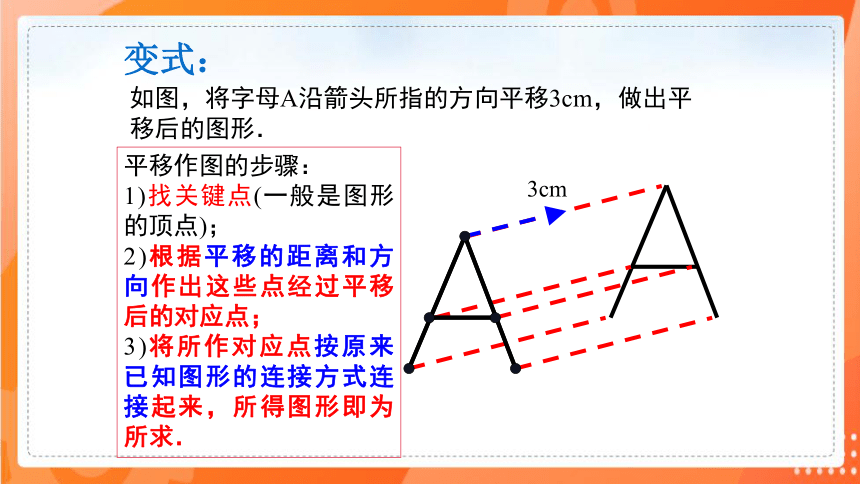
变式:
如图,将字母A沿箭头所指的方向平移3cm,做出平移后的图形.
3cm
平移作图的步骤:
1)找关键点(一般是图形的顶点);
2)根据平移的距离和方向作出这些点经过平移后的对应点;
3)将所作对应点按原来已知图形的连接方式连接起来,所得图形即为所求.
你还记得什么叫平移吗?
图形平移的性质是什么?
在平面内,把一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.
1.新图形与原图形形状和大小不变,但位置改变;
2.对应点的连线平行且相等.
知识回顾
二、平面直角坐标系中点的平移
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
根据左图回答问题:
1.将点A(-2,-3)向右平移5个单位长度,得到点A1( ___ , ___ );
2.将点A(-2,-3)向左平移
2个单位长度,得到点A2(____ , _____);
A1
-4
-3
3
-3
A2
y
x
合作与交流
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
3.将点A(-2,-3)向上平移4个单位长度,得到点A3( , );
4.将点A(-2,-3)向下平移2个单位长度,得到点A4( , ).
A3
A4
-2
1
-2
-5
y
x
你发现了什么?
向左平移a个单位对应点P2(x-a,y)
总结归纳
向右平移a个单位对应点 P1(x+a,y)
向上平移b个单位对应点P3(x,y+b)
向下平移b个单位对应点P4(x,y-b)
图形上的点P(x,y)
点的平移规律
典例精析
例3 平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8) B.(1,-2) C.(-6,-1) D.(0,-1)
点的平移变换:左右移动改变点的横坐标,左减右
加;上下移动改变点的纵坐标,下减上加.
归纳
C
解析:点A的坐标为(-3,-5),将点A向上平移4个单位,再向左平移3个单位到点B,点B的横坐标是-3-3=-6,纵坐标为-5+4=-1,即(-6,-1).
思考: (x,y) (x-3 , y+4)
A ( x, y )
B (x-3, y)
向左平移3个单位
向上平移4个单位
C (x-3, y+4)
A
B
C
A经过两次平移到C,能否经过 一次平移到C呢?
o
A
x
y
1 2 3 4 5 6 7 8 9 10
6
5
4
3
2
1
-1
-2
●
●
A’
问1:A点先向下平移2 个单位长度,再向右平移3个单位长度得到A’ 你能找到A’的位置吗?
合作探究
三、平面直角坐标系中坐标的二次平移
o
A
x
y
1 2 3 4 5 6 7 8 9 10
6
5
4
3
2
1
-1
-2
●
●
A’
问2:(1)你还能想到其他的平移方式吗?
(2)A点能否通过一次平移到达A’点的位置?若能,请指出平移方向和距离?
o
A
x
y
1 2 3 4 5 6 7 8 9 10
6
5
4
3
2
1
-1
-2
●
●
A’
问3:观察A点和A'点的坐标,有何变化?
A(2,1) A'(5,-1)
y
x
O
2
4
6
4
2
-2
-4
-2
8
A
画一画:将图中的“鱼”向下平移2个单位长度,再向右平移3个单位长度得到新“鱼”,试着在直角坐标系中画出新鱼.
问题1:在上述变化中,能否看成是经过一次平移得到的?如果能,请指出平移的方向和距离,并与同伴交流.
能
平移方向是O到A,平移距离是OA=
问题2:对应点的坐标之间有什么关系?
横坐标加3,纵坐标减2
做一做:先将右图中的“鱼” F的每个“顶点” 的横坐标分别加2,纵坐标不变,得到 “鱼” G;再将“鱼” G的每个“顶点” 的纵坐标分别加3,横坐标不变,得到“鱼” H.“鱼” H与原来的 “鱼” F相比有什么变化?能否将“鱼” H看成是“鱼” F经过一次平移得到的?与同伴交流.
1
2
3
4
5
6
7
8
0
–1
–2
–4
1
2
3
4
9
10
5
y
x
(6,-2)
(7,-1)
(7,1)
(5,0)
(7,4)
(2,0)
“鱼”G各“顶点”坐标
“鱼”F各 “顶点”坐标
(0,0)
(5,4)
(3,0)
(5,1)
(5,-1)
(4,-2)
“鱼”H各“顶点”坐标
(2,3)
(7,7)
(5,3)
(7,4)
(7,2)
(6,1)
1 “鱼”G各“顶点”坐标如下表:
2 “鱼”H各“顶点”坐标如下表:
F
G
H
结论:1.形状、大小相同,只是位置改变 ,先向右平移了2个单位长度,再向上平移了3个单位长度.
2.可以将“鱼”H看成是“鱼”F经过一次平移得到的,平移方向是点(0,0)到点(2,3)的方向,平移距离是 .
问题:在上述变化中,能否看成是经过一次平移得到的?如果能,请指出平移的方向和距离,并与同伴交流.
一个图形依次沿x轴方向、y轴方向平移后所得图形与原来的图形相比,位置有什么变化?它们对应点的坐标之间有怎样的关系?
交流讨论
平移方向和平移距离 对应点的坐标
向右平移a个单位长度,向上平移b个单位长度
向右平移a个单位长度,向下平移b个单位长度
向左平移a个单位长度,向上平移b个单位长度
向左平移a个单位长度,向下平移b个单位长度
(x+a , y+b)
(x+a , y-b)
(x-a , y+b)
(x-a , y-b)
一个图形依次沿x轴方向、y轴方向平移后所得图形,可以看成是由原来的图形经过一次平移得到的.
归纳总结
1. 在下面的六副图案中,(2)(3)(4)(5)(6)中的哪个图案可以通过平移图案(1)得到?
(3)
课堂练习
2. 如图,将字母 A 按箭头所指的方向平移 3 cm,作出平移后的图形.
3cm
3. 小明挪动家里的桌子,对应的四条腿移动的距离分别是:10.8 cm,11.1 cm,11.1 cm,11.2 cm,这样的挪动是平移吗?为什么?
不是,因为四个轮子移动的距离不相等,
与平移的定义不符.
4.如图,在平面直角坐标系中,将点M (2 , 1)向下平移2个单位长度得到点N,则点N 的坐标为( )
A.(2 , -1) B.(2 , 3)
C.(0 , 1) D.(4 , 1)
A
5.△ABC 在平面直角坐标系中的位置如图所示,任意一点P (a , b)经平移后得到点P1(a-2,b+3),将△ABC 作同样的平移得到△A1B1C1.
(1)求A1,B1,C1的坐标;
(2)指出这一平移的平移方向和
平移距离.
解:(1)∵原来点A的坐标为(1,1),点B的坐标为(-1,-1),点C的坐标为(4,-2),点P(a , b)经平移后得到点P1(a-2 , b+3),
∴A1(-1 , 4);B1(-3 , 2);C1(2 , 1);
(2)将△ABC平移得到△A1B1C1,平移的方向是射线AA1的方向,平移的距离为线段AA1的长度,AA1= ,即平移的距离为 个单位长度.
https://www.21cnjy.com/help/help_extract.php
北师大版八年级下册数学
第三章 图形的平移与旋转
3.1 图形的平移
这些物体的运动过程是否有共同点?
A
B
C
D
E
F
情景引入
在平面内,将一个图形沿 移动一定的距离,这样的图形运动称为平移.
图形平移的定义:
1
A
B
C
D
E
F
某个方向
一定的距离
图形的平移只改变图形的位置,不改变图形的形状和大小,即平移前后的两个图形全等.
2
一、平移的相关概念
说说你生活中见过的图形的平移例子
图形的平移的两个要素是:
同一方向 和 相同距离.
判断下面几组图形运动是不是平移?
3
A
C
D
B
×
×
√
×
ΔABC经过平移得到的ΔDEF,点A、B、C分别移到点D、E、F.
对应角:
对应点所连线段:
对应线段:
AB和DE,
AC和DF,
BC和EF
∠BAC和∠EDF,
∠ABC和∠DEF,
∠ACB和∠DFE
线段AD,
线段BE,
线段CF
对应点:
点A和点D,
点B和点E,
点C和点F
A
B
C
D
E
F
几何符号语言:
平移的两个图形全等;
对应点所连的线段平行(或在同一直线上)且相等;
对应线段平行(或在同一直线上)且相等;
对应角相等.
A
B
C
D
E
F
A
B
C
D
E
F
∵△ABC平移得到△DEF
∴△ABC≌△DEF
∵△ABC平移得到△DEF
∴AD∥BE ∥CF(或共线),
AD=BE =CF
∵△ABC平移得到△DEF
∴AB∥DE,AC∥DF,
BC ∥EF(或共线),
AB=DE,AC=DF,BC=EF
∵△ABC平移得到△DEF
∴∠BAC=∠EDF,
∠ABC=∠DEF,
∠ACB=∠DFE
平移的基本性质
如图,在ΔABC中,∠C=90°,∠ABC=30°,AB=4,将ΔABC沿射线PQ的方向平移5个单位长度后得到ΔA′B′C′,则
A
C
B
A′
C′
B′
P
Q
A′C′的长为 ;
∠B′A′C′的度数为 ;
四边形ABB′A′的周长为 .
2
60 °
18
练一练
例1 如图所示,经过平移,△ABC的顶点A移到了点C'.画出平移后的△A'B'C'的位置.
并指出平移的方向和距离.
A
B
C
(1)连接CC';
(2)分别过点B,C按射线CC'的方向作线段BB',AA',使得它们与线段CC'平行且相等,连接A'C',A'B',B'C',△A'B'C'为所求;
(3)平移的方向就是点C到点C'的方向;
(4)平移的距离就是线段AA'的长度.
典例精析
B
C
A
例2:如图,经过平移,ΔABC的顶点A移到了点D,作出平移后的三角形.
E
F
D
解:如图,连接AD,过B、C点分别做线段BE、CF使得他们与线段AD平行且相等,连接 DE、DF、EF,ΔDEF就是ΔABC平移后的图形.
B
C
A
想一想:有其他的方法吗?
E
F
D
解:如图,过点D按射线AB的方向做线段DE平行且等于AB;过点D按射线AC的方向做线段DF平行且等于AC;连接EF. ΔDEF 就是ΔABC平移后的图形.
变式:
如图,将字母A沿箭头所指的方向平移3cm,做出平移后的图形.
3cm
平移作图的步骤:
1)找关键点(一般是图形的顶点);
2)根据平移的距离和方向作出这些点经过平移后的对应点;
3)将所作对应点按原来已知图形的连接方式连接起来,所得图形即为所求.
你还记得什么叫平移吗?
图形平移的性质是什么?
在平面内,把一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.
1.新图形与原图形形状和大小不变,但位置改变;
2.对应点的连线平行且相等.
知识回顾
二、平面直角坐标系中点的平移
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
根据左图回答问题:
1.将点A(-2,-3)向右平移5个单位长度,得到点A1( ___ , ___ );
2.将点A(-2,-3)向左平移
2个单位长度,得到点A2(____ , _____);
A1
-4
-3
3
-3
A2
y
x
合作与交流
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
O
1
3.将点A(-2,-3)向上平移4个单位长度,得到点A3( , );
4.将点A(-2,-3)向下平移2个单位长度,得到点A4( , ).
A3
A4
-2
1
-2
-5
y
x
你发现了什么?
向左平移a个单位对应点P2(x-a,y)
总结归纳
向右平移a个单位对应点 P1(x+a,y)
向上平移b个单位对应点P3(x,y+b)
向下平移b个单位对应点P4(x,y-b)
图形上的点P(x,y)
点的平移规律
典例精析
例3 平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8) B.(1,-2) C.(-6,-1) D.(0,-1)
点的平移变换:左右移动改变点的横坐标,左减右
加;上下移动改变点的纵坐标,下减上加.
归纳
C
解析:点A的坐标为(-3,-5),将点A向上平移4个单位,再向左平移3个单位到点B,点B的横坐标是-3-3=-6,纵坐标为-5+4=-1,即(-6,-1).
思考: (x,y) (x-3 , y+4)
A ( x, y )
B (x-3, y)
向左平移3个单位
向上平移4个单位
C (x-3, y+4)
A
B
C
A经过两次平移到C,能否经过 一次平移到C呢?
o
A
x
y
1 2 3 4 5 6 7 8 9 10
6
5
4
3
2
1
-1
-2
●
●
A’
问1:A点先向下平移2 个单位长度,再向右平移3个单位长度得到A’ 你能找到A’的位置吗?
合作探究
三、平面直角坐标系中坐标的二次平移
o
A
x
y
1 2 3 4 5 6 7 8 9 10
6
5
4
3
2
1
-1
-2
●
●
A’
问2:(1)你还能想到其他的平移方式吗?
(2)A点能否通过一次平移到达A’点的位置?若能,请指出平移方向和距离?
o
A
x
y
1 2 3 4 5 6 7 8 9 10
6
5
4
3
2
1
-1
-2
●
●
A’
问3:观察A点和A'点的坐标,有何变化?
A(2,1) A'(5,-1)
y
x
O
2
4
6
4
2
-2
-4
-2
8
A
画一画:将图中的“鱼”向下平移2个单位长度,再向右平移3个单位长度得到新“鱼”,试着在直角坐标系中画出新鱼.
问题1:在上述变化中,能否看成是经过一次平移得到的?如果能,请指出平移的方向和距离,并与同伴交流.
能
平移方向是O到A,平移距离是OA=
问题2:对应点的坐标之间有什么关系?
横坐标加3,纵坐标减2
做一做:先将右图中的“鱼” F的每个“顶点” 的横坐标分别加2,纵坐标不变,得到 “鱼” G;再将“鱼” G的每个“顶点” 的纵坐标分别加3,横坐标不变,得到“鱼” H.“鱼” H与原来的 “鱼” F相比有什么变化?能否将“鱼” H看成是“鱼” F经过一次平移得到的?与同伴交流.
1
2
3
4
5
6
7
8
0
–1
–2
–4
1
2
3
4
9
10
5
y
x
(6,-2)
(7,-1)
(7,1)
(5,0)
(7,4)
(2,0)
“鱼”G各“顶点”坐标
“鱼”F各 “顶点”坐标
(0,0)
(5,4)
(3,0)
(5,1)
(5,-1)
(4,-2)
“鱼”H各“顶点”坐标
(2,3)
(7,7)
(5,3)
(7,4)
(7,2)
(6,1)
1 “鱼”G各“顶点”坐标如下表:
2 “鱼”H各“顶点”坐标如下表:
F
G
H
结论:1.形状、大小相同,只是位置改变 ,先向右平移了2个单位长度,再向上平移了3个单位长度.
2.可以将“鱼”H看成是“鱼”F经过一次平移得到的,平移方向是点(0,0)到点(2,3)的方向,平移距离是 .
问题:在上述变化中,能否看成是经过一次平移得到的?如果能,请指出平移的方向和距离,并与同伴交流.
一个图形依次沿x轴方向、y轴方向平移后所得图形与原来的图形相比,位置有什么变化?它们对应点的坐标之间有怎样的关系?
交流讨论
平移方向和平移距离 对应点的坐标
向右平移a个单位长度,向上平移b个单位长度
向右平移a个单位长度,向下平移b个单位长度
向左平移a个单位长度,向上平移b个单位长度
向左平移a个单位长度,向下平移b个单位长度
(x+a , y+b)
(x+a , y-b)
(x-a , y+b)
(x-a , y-b)
一个图形依次沿x轴方向、y轴方向平移后所得图形,可以看成是由原来的图形经过一次平移得到的.
归纳总结
1. 在下面的六副图案中,(2)(3)(4)(5)(6)中的哪个图案可以通过平移图案(1)得到?
(3)
课堂练习
2. 如图,将字母 A 按箭头所指的方向平移 3 cm,作出平移后的图形.
3cm
3. 小明挪动家里的桌子,对应的四条腿移动的距离分别是:10.8 cm,11.1 cm,11.1 cm,11.2 cm,这样的挪动是平移吗?为什么?
不是,因为四个轮子移动的距离不相等,
与平移的定义不符.
4.如图,在平面直角坐标系中,将点M (2 , 1)向下平移2个单位长度得到点N,则点N 的坐标为( )
A.(2 , -1) B.(2 , 3)
C.(0 , 1) D.(4 , 1)
A
5.△ABC 在平面直角坐标系中的位置如图所示,任意一点P (a , b)经平移后得到点P1(a-2,b+3),将△ABC 作同样的平移得到△A1B1C1.
(1)求A1,B1,C1的坐标;
(2)指出这一平移的平移方向和
平移距离.
解:(1)∵原来点A的坐标为(1,1),点B的坐标为(-1,-1),点C的坐标为(4,-2),点P(a , b)经平移后得到点P1(a-2 , b+3),
∴A1(-1 , 4);B1(-3 , 2);C1(2 , 1);
(2)将△ABC平移得到△A1B1C1,平移的方向是射线AA1的方向,平移的距离为线段AA1的长度,AA1= ,即平移的距离为 个单位长度.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
