北师大版八下数学6.4多边形的内角和与外角和 课件(18张ppt)
文档属性
| 名称 | 北师大版八下数学6.4多边形的内角和与外角和 课件(18张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 646.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 09:23:47 | ||
图片预览






文档简介
(共18张PPT)
*
感谢您的关注!
义务教育课程标准实验教科书---北师版
6.4多边形的内角和与外角和(2)
八年级(下)
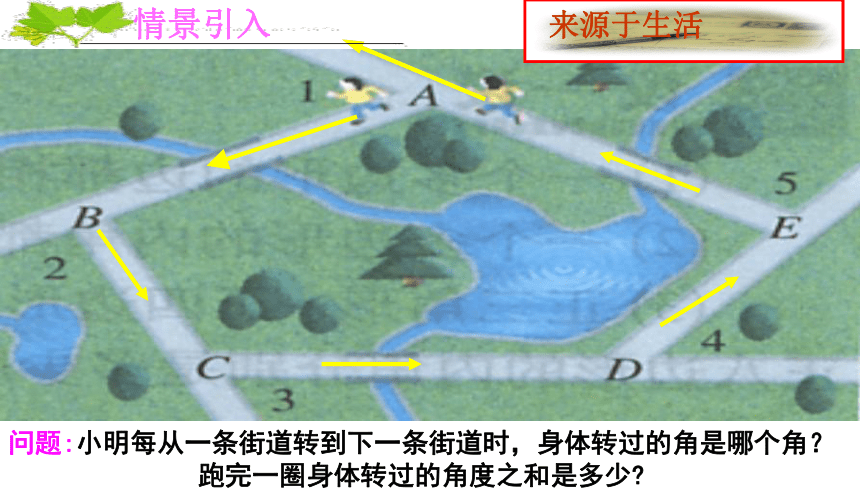
问题:小明每从一条街道转到下一条街道时,身体转过的角是哪个角?跑完一圈身体转过的角度之和是多少
情景引入
来源于生活
1. 了解多边形的外角定义,并能准确找出多边形的外角;
2. 经历探索多边形的外角和公式的过程;会应用公式解决实际问题.
学习目标:
1. n边形的内角和为____ 正n边形的一个内角为 ____
2. ________叫做这个多边形的外角(exterior angle)
尝试画一下五边形的外角
3.n边形有___个外角.正多边形的每一个外角都_______.
4. ____________叫做这个多边形的外角和.
5.通过预习猜想:三角形外角和为:___;
四边形外角和为:___;五边形外角和为:___
八边形外角和为: ___ ……n边形外角和为: ___
预习检查:
1
2
3
4
5
1.一个多边形的内角和是外角和的2倍,
它是几边形?
2.若多边形的边数增加,则其外角和的度数( )
A 增加 B 减少 C 不变 D 无法确定
尝试练习:
想一想:
问题: 1)上面每个图形的内角相等吗?分别是多少度
2)上图中的外角是哪些 它们相等吗
3)上图中外角和分别是多少
你能行!
等边三角形
1
2
1
1
正方形
正六边形
3
2
3
4
2
3
4
5
6
60
90
120
如果是六边形、八边形,那么还有类似的结论吗?
互动探究,合作交流:
活动一
你知道下列多边形的外角和是多少吗 说说你的方法.
结论:任意多边形的外角和等于360 。
多边形的外角和与多边形的边数无关,它恒等于360°.
注意
1
1
2
2
3
3
4
1
2
3
4
5
试一试:
你知道验证多边形外角和结论有几种方法吗?
归纳
①剪拼方式 ②平移方式
③测量方式 ④拖动方式
⑤缩放方式 ⑥圆周方式
⑦推理方式
问题解决:
服务于生活
[例1]一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和是
(n-2)·180°,外角和等于360°,
所以:(n-2)·180=3×360
解得:n=8
答:这个多边形是八边形.
例题赏析:
[例2]一个正多边形的一个内角比相邻的外角大36 ,求这个正多边形的边数.
例题赏析:
解:设这个正多边形的一个外角是x,则与它相邻的内角 是180-x
所以: 180-x = x+36
解得:x=72
360÷72=5
答:这个多边形是五边形.
1 .一个多边形的内角和比它的外角和的3倍少
180 °,这个多边形的边数为( )
A. 5 B. 6 C. 7 D. 8
巩固练习:
4.下列多边形中,内角和与外角和相等的是( )
A.四边形 B.五边形 C.六边形 D.八边形
5.若一个n边形的内角都相等,且内角的度数与和它相邻的外角的度数比为3∶1,那么,这个多边形的边数为________.
2. 一个多边形的每个外角都是120°,则这个多边形是____边形.
3.多边形的内角与相邻外角的和为_________
1.一个多边形的内角和与外角和为540°,则它是 形.
2.多边形内角和与外角和之比是5:2,则n= .
3.一个多边形最少可分割成五个三角形,则它是____边形( )
A.8 B.7 C.6 D.5
4.一个多边形的外角和是内角和的一半,则它是边形( )
A.7 B.6 C.5 D.4
5.一个正多边形,它的一个外角等于它的相邻的内角的 ,则 这个多边形是( ).
A.正十二边形 B. 正十边形 C.正八边形 D.正六边形
达标检测:
每小题30分
拓展延伸:
1. 已知多边形的内角和与某一个外角的度数总和为1350°,求多边形的边数.
2.已知,如图,∠A=∠C=90°,对角线BE、DF分别平分∠ABC和∠ADC,BE和DF平行吗?说明你的理由.
“多边形的外角和就像圆一样,圈住了
我们的欢笑,也圈住了我们的记忆”这句
话借用了多边形的外角和的性质,形象
地表达了多边形外角和恒等于360 。
生活百味:
议一议:
动动脑
你能运用多边形内角和结论
推导出多边形外角和结论吗?
∵ n边形的每一个外角与它相邻的内角的和是_____
∴ n边形的内角和加外角和等于 ________
∵ n 边形的内角和等于 ___________
∴ n 边形的外角和等于
n 180 – (n-2) 180 = 360 。
180 ,
n 180 ,
(n-2) 180 ,
本节课你有
什么收获?
回味无穷:
*
感谢您的关注!
义务教育课程标准实验教科书---北师版
6.4多边形的内角和与外角和(2)
八年级(下)
问题:小明每从一条街道转到下一条街道时,身体转过的角是哪个角?跑完一圈身体转过的角度之和是多少
情景引入
来源于生活
1. 了解多边形的外角定义,并能准确找出多边形的外角;
2. 经历探索多边形的外角和公式的过程;会应用公式解决实际问题.
学习目标:
1. n边形的内角和为____ 正n边形的一个内角为 ____
2. ________叫做这个多边形的外角(exterior angle)
尝试画一下五边形的外角
3.n边形有___个外角.正多边形的每一个外角都_______.
4. ____________叫做这个多边形的外角和.
5.通过预习猜想:三角形外角和为:___;
四边形外角和为:___;五边形外角和为:___
八边形外角和为: ___ ……n边形外角和为: ___
预习检查:
1
2
3
4
5
1.一个多边形的内角和是外角和的2倍,
它是几边形?
2.若多边形的边数增加,则其外角和的度数( )
A 增加 B 减少 C 不变 D 无法确定
尝试练习:
想一想:
问题: 1)上面每个图形的内角相等吗?分别是多少度
2)上图中的外角是哪些 它们相等吗
3)上图中外角和分别是多少
你能行!
等边三角形
1
2
1
1
正方形
正六边形
3
2
3
4
2
3
4
5
6
60
90
120
如果是六边形、八边形,那么还有类似的结论吗?
互动探究,合作交流:
活动一
你知道下列多边形的外角和是多少吗 说说你的方法.
结论:任意多边形的外角和等于360 。
多边形的外角和与多边形的边数无关,它恒等于360°.
注意
1
1
2
2
3
3
4
1
2
3
4
5
试一试:
你知道验证多边形外角和结论有几种方法吗?
归纳
①剪拼方式 ②平移方式
③测量方式 ④拖动方式
⑤缩放方式 ⑥圆周方式
⑦推理方式
问题解决:
服务于生活
[例1]一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和是
(n-2)·180°,外角和等于360°,
所以:(n-2)·180=3×360
解得:n=8
答:这个多边形是八边形.
例题赏析:
[例2]一个正多边形的一个内角比相邻的外角大36 ,求这个正多边形的边数.
例题赏析:
解:设这个正多边形的一个外角是x,则与它相邻的内角 是180-x
所以: 180-x = x+36
解得:x=72
360÷72=5
答:这个多边形是五边形.
1 .一个多边形的内角和比它的外角和的3倍少
180 °,这个多边形的边数为( )
A. 5 B. 6 C. 7 D. 8
巩固练习:
4.下列多边形中,内角和与外角和相等的是( )
A.四边形 B.五边形 C.六边形 D.八边形
5.若一个n边形的内角都相等,且内角的度数与和它相邻的外角的度数比为3∶1,那么,这个多边形的边数为________.
2. 一个多边形的每个外角都是120°,则这个多边形是____边形.
3.多边形的内角与相邻外角的和为_________
1.一个多边形的内角和与外角和为540°,则它是 形.
2.多边形内角和与外角和之比是5:2,则n= .
3.一个多边形最少可分割成五个三角形,则它是____边形( )
A.8 B.7 C.6 D.5
4.一个多边形的外角和是内角和的一半,则它是边形( )
A.7 B.6 C.5 D.4
5.一个正多边形,它的一个外角等于它的相邻的内角的 ,则 这个多边形是( ).
A.正十二边形 B. 正十边形 C.正八边形 D.正六边形
达标检测:
每小题30分
拓展延伸:
1. 已知多边形的内角和与某一个外角的度数总和为1350°,求多边形的边数.
2.已知,如图,∠A=∠C=90°,对角线BE、DF分别平分∠ABC和∠ADC,BE和DF平行吗?说明你的理由.
“多边形的外角和就像圆一样,圈住了
我们的欢笑,也圈住了我们的记忆”这句
话借用了多边形的外角和的性质,形象
地表达了多边形外角和恒等于360 。
生活百味:
议一议:
动动脑
你能运用多边形内角和结论
推导出多边形外角和结论吗?
∵ n边形的每一个外角与它相邻的内角的和是_____
∴ n边形的内角和加外角和等于 ________
∵ n 边形的内角和等于 ___________
∴ n 边形的外角和等于
n 180 – (n-2) 180 = 360 。
180 ,
n 180 ,
(n-2) 180 ,
本节课你有
什么收获?
回味无穷:
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
