华东师大版七年级下册数学 10.3.2 旋转的特征 教案
文档属性
| 名称 | 华东师大版七年级下册数学 10.3.2 旋转的特征 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 155.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 09:37:17 | ||
图片预览

文档简介
10.3.2旋转的特征
教学目标
1.理解图形旋转后,图形中每一点都绕着旋转中心旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状和大小都没有发生变化。
2.会画已知图形绕某一点旋转一定角度后的图形。
3.能找出旋转后的旋转中心,旋转的角度,对应角,对应线段。
4.能从现实生活中发现并提出简单的数学问题。
教学重难点
重点:旋转特征及其应用。
难点:旋转中心,旋转角度,画旋转图形。
学情分析:学生已经掌握了旋转概念和旋转要素,及会找出旋转前后对应点、对应角、对应线段;并养成了通过观察得结论的习惯;但是用准确语言归纳结论的能力有待加强,这节课继续培养;应用知识到实际是这这节课的重点和难点,通过练习完成。
教学过程
一、知识回顾
旋转概念:在同一平面内,讲一个图形绕着一个定点沿某个方向转动一个角度的运动叫旋转运动,简称旋转。
旋转要素:旋转中心、旋转方向、旋转角。
二、探究新知
(一)、观察三个图形,得出结论。
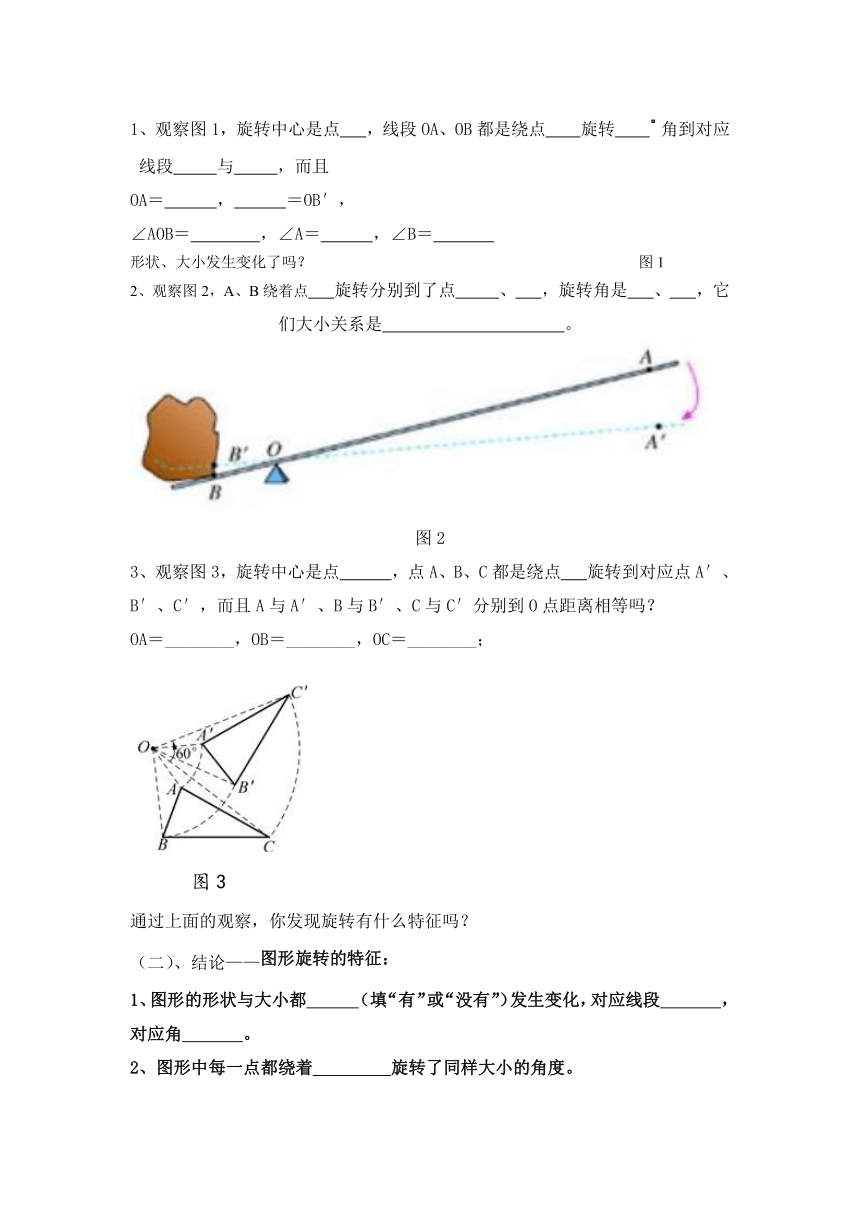
1、观察图1,旋转中心是点 ,线段OA、OB都是绕点 旋转 角到对应线段 与 ,而且
OA= , =OB′,
∠AOB= ,∠A= ,∠B=
形状、大小发生变化了吗? 图1
2、观察图2,A、B绕着点 旋转分别到了点 、 ,旋转角是 、 ,它们大小关系是 。 图2
3、观察图3,旋转中心是点 ,点A、B、C都是绕点 旋转到对应点A′、B′、C′,而且A与A′、B与B′、C与C′分别到O点距离相等吗?
OA=________,OB=________,OC=________;
图3
通过上面的观察,你发现旋转有什么特征吗?
(二)、结论——图形旋转的特征:
1、图形的形状与大小都 (填“有”或“没有”)发生变化,对应线段 ,对应角 。
2、图形中每一点都绕着 旋转了同样大小的角度。
3、对应点到旋转中心的距离 。
三、旋转特征的应用
1、画原图形旋转后的图形
(1)、画出△ABC绕点C逆时针旋转90后的图形。
(2)、画出所给图形绕点O顺时针旋转90°后的图形.旋转几次后可以与原图形重合
2、找图形中的相等线段和相等角
(1)、如图1,正方形ABCD中,∠BAD=∠ABC=∠C=∠D=90°,AB=BC=CD=DA边DC上有一点E,将△ADE旋转后得到了△ABG;旋转中心是________,旋转了_______度。
(2)、如图2,△ABC按逆时针方向绕点O旋转了60°后成为△DEF,那么
OA=_____,OB=______,∠COF=_____度, ∠AOD=_____度, ∠A=_____,∠C=______,AB=_____, BC=______。
(3)、如图3,△ABC按逆时针方向转动了80°以后成为△A/B/C/,已知∠B=60度,∠C=55度,那么∠BAC/= 度。
图1 图2 图3
3、如图4,△DEF是由△ABC旋转得到的,请作出它的旋转中心。
图4
4、如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,试作出
△ABC绕点D顺时针旋转90°所得的图形。并指出图形中有多少个等腰直角三角形。
四、课堂小结。
这节课你有什么收获 学到了什么 还有哪些需老师帮助解决的问题
五、布置作业 。
导学案第三学时。
板书设计:
10.3.3 旋转的特征
图形旋转的特征:
1、图形中每一个点都绕着旋转中心旋转了同样大小的角度.
2、对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状与大小都没有发生变化.
教学目标
1.理解图形旋转后,图形中每一点都绕着旋转中心旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状和大小都没有发生变化。
2.会画已知图形绕某一点旋转一定角度后的图形。
3.能找出旋转后的旋转中心,旋转的角度,对应角,对应线段。
4.能从现实生活中发现并提出简单的数学问题。
教学重难点
重点:旋转特征及其应用。
难点:旋转中心,旋转角度,画旋转图形。
学情分析:学生已经掌握了旋转概念和旋转要素,及会找出旋转前后对应点、对应角、对应线段;并养成了通过观察得结论的习惯;但是用准确语言归纳结论的能力有待加强,这节课继续培养;应用知识到实际是这这节课的重点和难点,通过练习完成。
教学过程
一、知识回顾
旋转概念:在同一平面内,讲一个图形绕着一个定点沿某个方向转动一个角度的运动叫旋转运动,简称旋转。
旋转要素:旋转中心、旋转方向、旋转角。
二、探究新知
(一)、观察三个图形,得出结论。
1、观察图1,旋转中心是点 ,线段OA、OB都是绕点 旋转 角到对应线段 与 ,而且
OA= , =OB′,
∠AOB= ,∠A= ,∠B=
形状、大小发生变化了吗? 图1
2、观察图2,A、B绕着点 旋转分别到了点 、 ,旋转角是 、 ,它们大小关系是 。 图2
3、观察图3,旋转中心是点 ,点A、B、C都是绕点 旋转到对应点A′、B′、C′,而且A与A′、B与B′、C与C′分别到O点距离相等吗?
OA=________,OB=________,OC=________;
图3
通过上面的观察,你发现旋转有什么特征吗?
(二)、结论——图形旋转的特征:
1、图形的形状与大小都 (填“有”或“没有”)发生变化,对应线段 ,对应角 。
2、图形中每一点都绕着 旋转了同样大小的角度。
3、对应点到旋转中心的距离 。
三、旋转特征的应用
1、画原图形旋转后的图形
(1)、画出△ABC绕点C逆时针旋转90后的图形。
(2)、画出所给图形绕点O顺时针旋转90°后的图形.旋转几次后可以与原图形重合
2、找图形中的相等线段和相等角
(1)、如图1,正方形ABCD中,∠BAD=∠ABC=∠C=∠D=90°,AB=BC=CD=DA边DC上有一点E,将△ADE旋转后得到了△ABG;旋转中心是________,旋转了_______度。
(2)、如图2,△ABC按逆时针方向绕点O旋转了60°后成为△DEF,那么
OA=_____,OB=______,∠COF=_____度, ∠AOD=_____度, ∠A=_____,∠C=______,AB=_____, BC=______。
(3)、如图3,△ABC按逆时针方向转动了80°以后成为△A/B/C/,已知∠B=60度,∠C=55度,那么∠BAC/= 度。
图1 图2 图3
3、如图4,△DEF是由△ABC旋转得到的,请作出它的旋转中心。
图4
4、如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,试作出
△ABC绕点D顺时针旋转90°所得的图形。并指出图形中有多少个等腰直角三角形。
四、课堂小结。
这节课你有什么收获 学到了什么 还有哪些需老师帮助解决的问题
五、布置作业 。
导学案第三学时。
板书设计:
10.3.3 旋转的特征
图形旋转的特征:
1、图形中每一个点都绕着旋转中心旋转了同样大小的角度.
2、对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状与大小都没有发生变化.
