函数的单调性

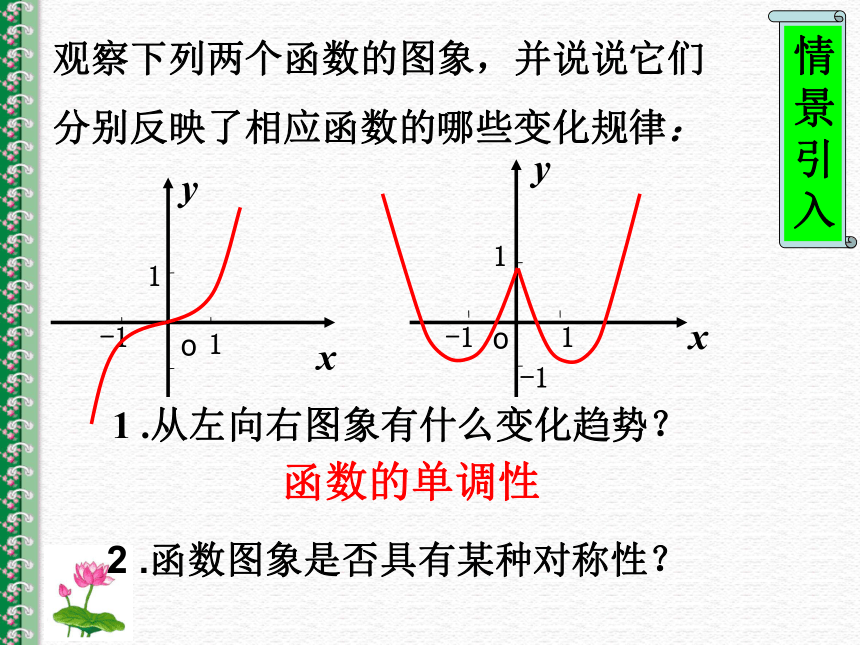
课件23张PPT。§1.3.1 函数的单调性yyxxoo11-111-1-1观察下列两个函数的图象，并说说它们
分别反映了相应函数的哪些变化规律：
1 .从左向右图象有什么变化趋势？
2 .函数图象是否具有某种对称性？ 函数的单调性xyo-1xOy1124-1-21 1.从左至右图象————
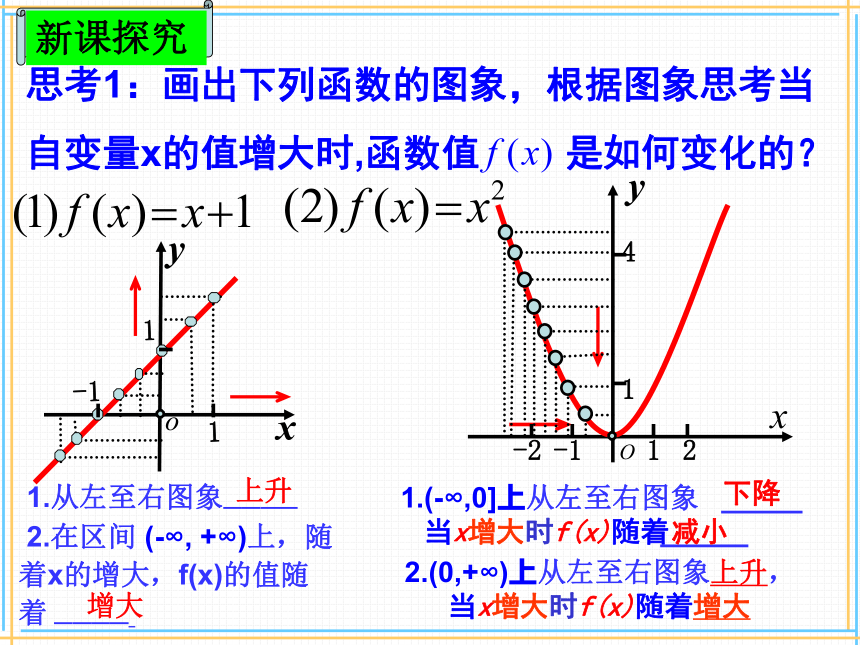
2.在区间 (-∞, +∞)上，随着x的增大，f(x)的值随着 ———— 2.(0,+∞)上从左至右图象上升，
当x增大时f(x)随着增大 1上升增大下降 减小思考1：画出下列函数的图象，根据图象思考当
自变量x的值增大时,函数值 是如何变化的？xyo-1xOy1124-1-211 在某一区间内，
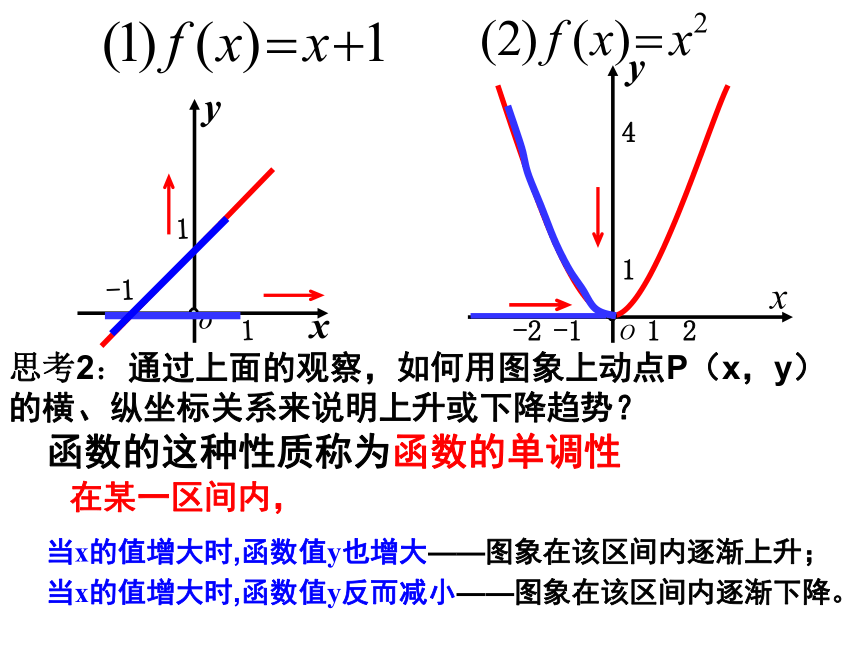
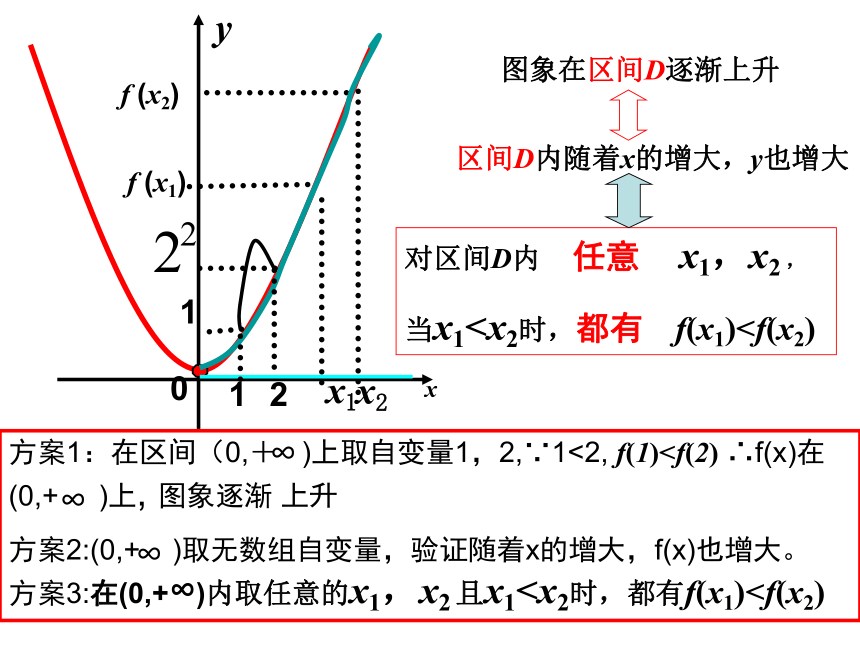
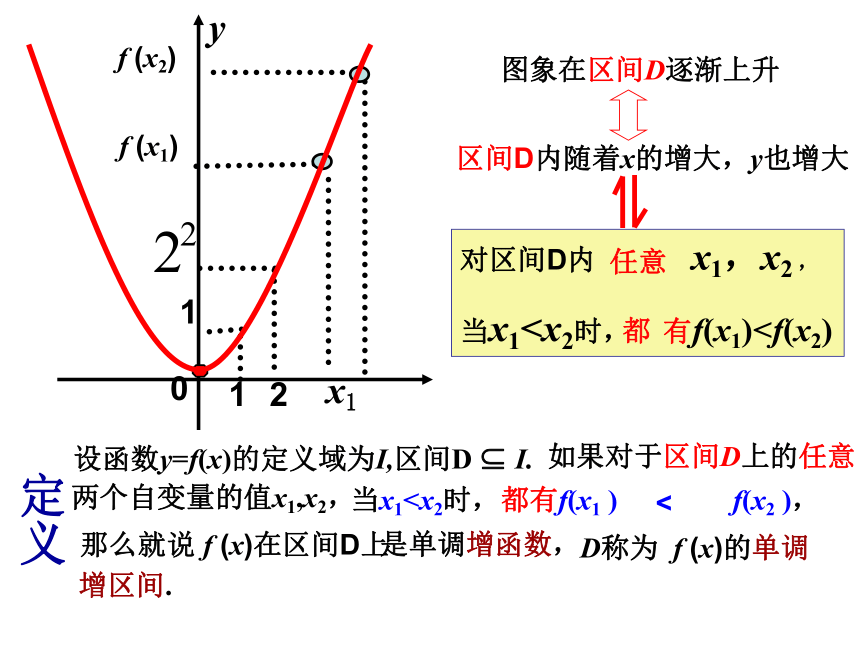
当x的值增大时,函数值y也增大——图象在该区间内逐渐上升；当x的值增大时,函数值y反而减小——图象在该区间内逐渐下降。函数的这种性质称为函数的单调性思考2：通过上面的观察，如何用图象上动点P（x，y）的横、纵坐标关系来说明上升或下降趋势？思考3：如何用数学符号描述这种上升趋势？对区间D内 任意 x1，x2 ，
当x1当x1 任意区间D内随着x的增大，y也增大图象在区间D逐渐上升0 x1f (x1)f (x2)y 那么就说在f(x)这个区间上是单调
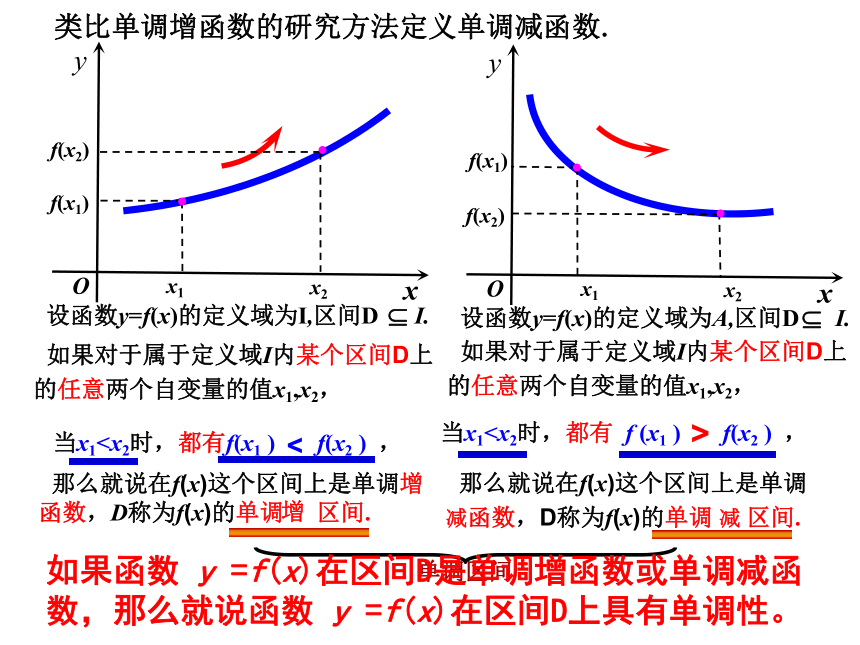
减函数，D称为f(x)的单调 减 区间.类比单调增函数的研究方法定义单调减函数.x 如果对于属于定义域I内某个区间D上
的任意两个自变量的值x1,x2， 如果对于属于定义域I内某个区间D上
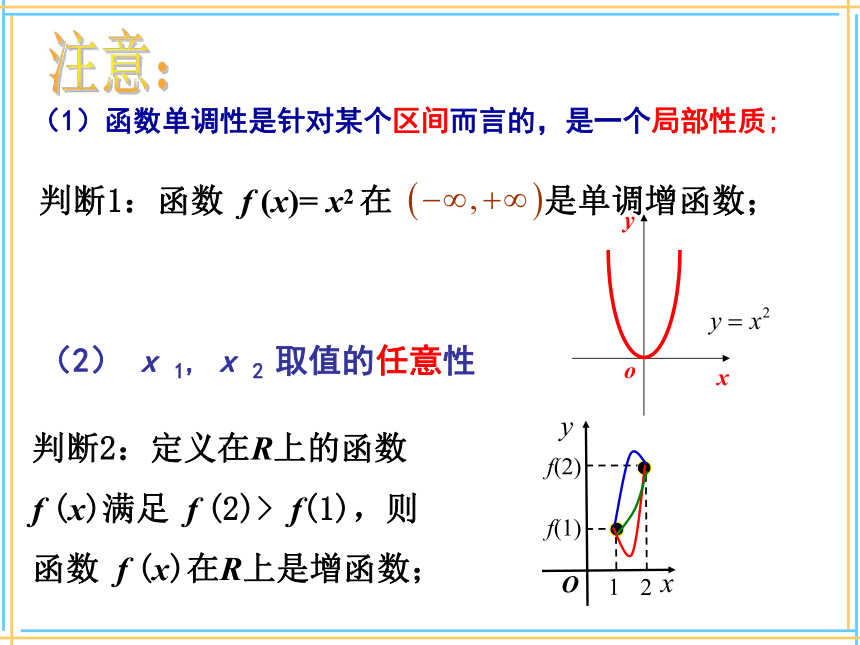
的任意两个自变量的值x1,x2， 那么就说在f(x)这个区间上是单调增 函数，D称为f(x)的单调 区间.增当x1单调区间如果函数 y =f(x)在区间D是单调增函数或单调减函数，那么就说函数 y =f(x)在区间D上具有单调性。（1）函数单调性是针对某个区间而言的，是一个局部性质;注意：（2） x 1, x 2 取值的任意性判断2：定义在R上的函数
f (x)满足 f (2)> f(1)，则
函数 f (x)在R上是增函数；解:函数y=f(x)的单调区间有[－5,－2）,[－2,1) ，[1，3), [3，5].例1. 如图是定义在闭区间[－5,5]上的函数 y = f(x)的图象, 根据图象说出函数的单调区间, 以及在每一单调区间上, 函数是增函数还是减函数？ 其中y=f(x)在区间[－2，1)，[3，5]上是增函数；说明:1.区间端点处若有定义写开写闭均可.
2.图象法判断函数的单调性：从左向右看图象的升降情况
练一练
根据下图说出函数的单调区间，以及在每一单调区间上，函数是增函数还是减函数.


2544xyO-1321解:函数y=f(x)的单调区间有[－1,0）,[0,2) ，[2，4), [4，5].其中y=f(x)在区间[0，2)，[4，5]上是增函数；在区间[－1，0），[2，4)上是减函数.证明:12341.设量(自变量);2.作差变形;3.判断;4.结(论)用定义证明函数单调性的四步骤：（1）设量:在所给区间上任意设两个实 数 （2）作差
（3）变形 作差
：常通过“因式分解”、“通分”、“配方”等
手段将差式变形为因式乘积或平方和形式 判断 的符号（4）结论:并作出单调性的结论证明函数　　　 在R上是减函数.练一练.利用定义：∴函数 在R上是减函数．则画出函数 图象，写出定义域并写出单调区间：_____________ ,讨论：根据函数单调性的定义yOx 在 (0,+∞) 上任取 x1、 x2
当x1< x2时，都有f(x1) f(x2)>yOx-11-11 取自变量－1< 1，
而 f(－1) f(1)<逗号隔开 巩固1. 两个定义：增函数、减函数的定义；3.一个数学思想：数形结合2：两种方法如何确定函数的单调区间？选做题：作业:（必做）课本39页A组第1、 2题 谢谢！巩固练习1、定义在R上的函数对任意两个不相等实数总有 成立，则必有（ ）
A、函数是先增加后减少 B、函数是先减少后增加
C、在R上是增函数 D、在R上是减函数
2．函数y＝ －6x＋10在区间（2，4）上是（　　）
A．递减函数 B．递增函数
C．先递减再递增 D．选递增再递减．
3．设函数f (x)是R上的减函数，又若a R，则 （ ）
A． f (a)>f (2a) B ．f ( ) C ．f ( +a)5.证明函数在 是增函数(1,+∞)