2.3.2《双曲线及其标准方程》
图片预览





文档简介
课件21张PPT。2.3.2双曲线及其
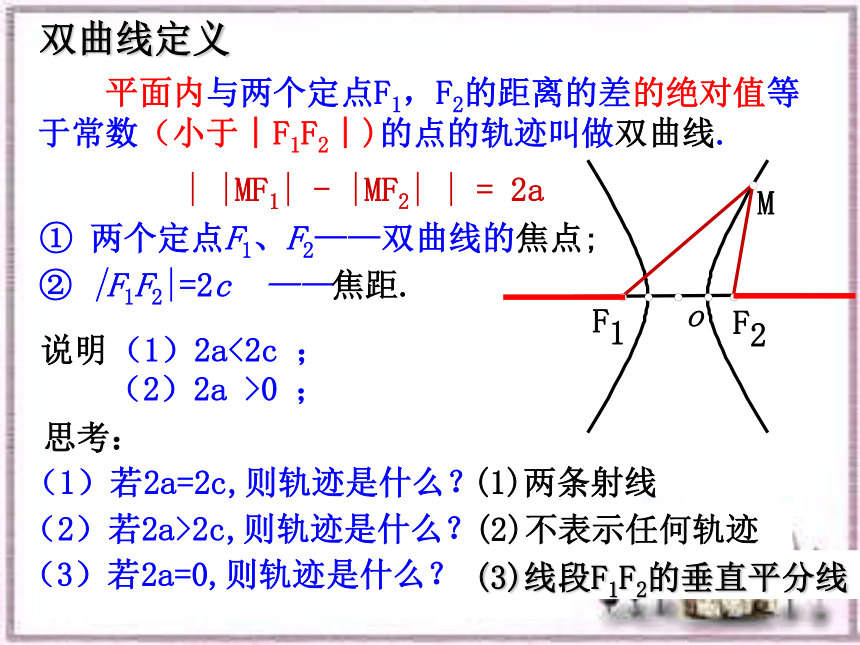
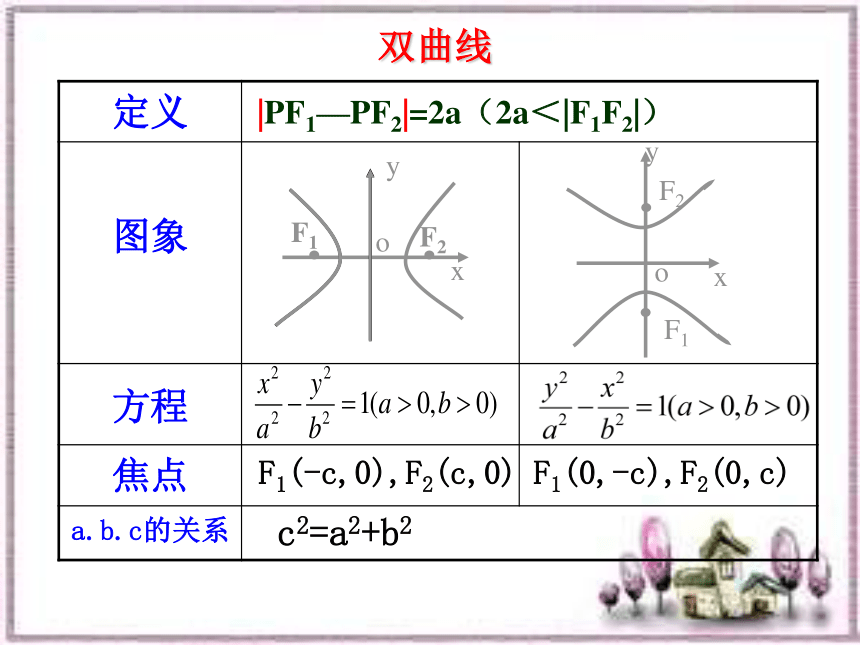
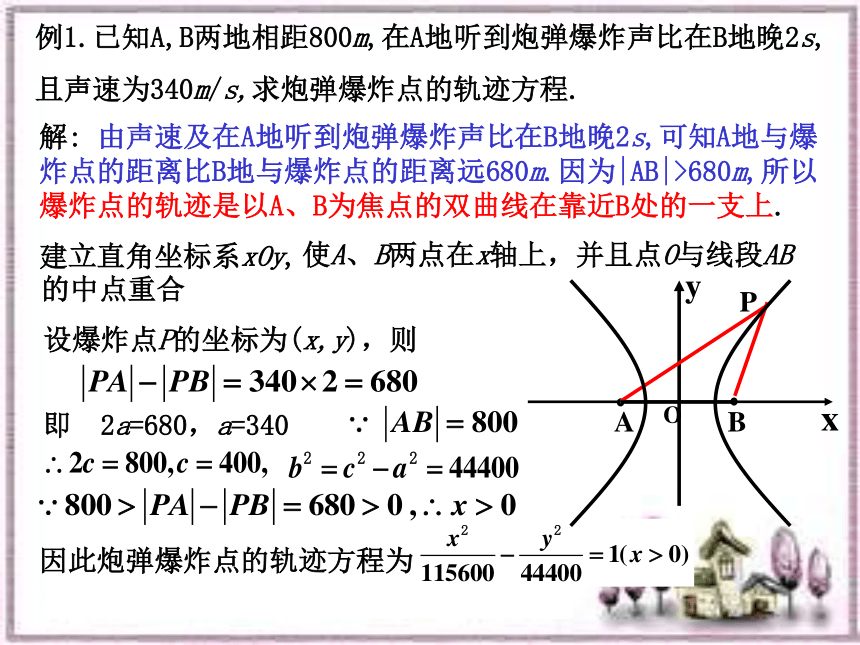
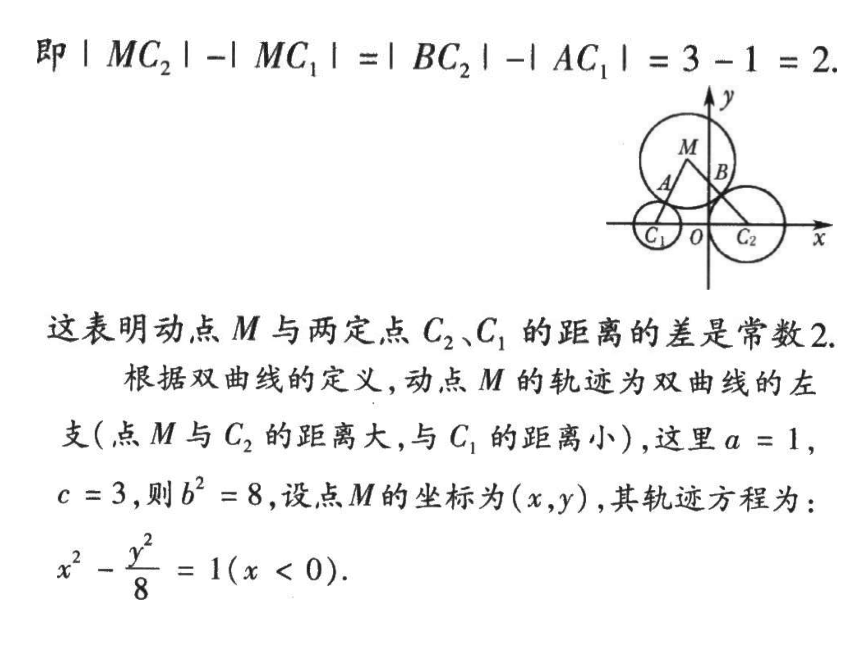
标准方程① 两个定点F1、F2——双曲线的焦点;② |F1F2|=2c ——焦距.(1)2a<2c ; 平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于︱F1F2︱)的点的轨迹叫做双曲线.(2)2a >0 ;双曲线定义思考:(1)若2a=2c,则轨迹是什么?(2)若2a>2c,则轨迹是什么?说明(3)若2a=0,则轨迹是什么? | |MF1| - |MF2| | = 2a(1)两条射线(2)不表示任何轨迹(3)线段F1F2的垂直平分线F1F2yxoyoxF1F2|PF1—PF2|=2a(2a<|F1F2|)F1(-c,0),F2(c,0)F1(0,-c),F2(0,c)c2=a2+b2双曲线 使A、B两点在x轴上,并且点O与线段AB的中点重合解: 由声速及在A地听到炮弹爆炸声比在B地晚2s,可知A地与爆炸点的距离比B地与爆炸点的距离远680m.因为|AB|>680m,所以爆炸点的轨迹是以A、B为焦点的双曲线在靠近B处的一支上.例1.已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.建立直角坐标系xOy,设爆炸点P的坐标为(x,y),则即 2a=680,a=340因此炮弹爆炸点的轨迹方程为答:再增设一个观测点C,利用B、C(或A、C)两处测得的爆炸声的时间差,可以求出另一个双曲线的方程,解这两个方程组成的方程组,就能确定爆炸点的准确位置.这是双曲线的一个重要应用.其实全球定位系统就是根据例2这个原理来定位的解: 在△ABC中,|BC|=10,故顶点A的轨迹是以B、C为焦点的双曲线的左支又因c=5,a=3,则b=4则顶点A的轨迹方程为例3:根据下列条件,求双曲线的标准方程例4.如图,点A,B的坐标分别是(-5,0),(5,0),直线AM,BM相交于点M,且它们斜率之积是4/9,试求点M的轨迹方程,并由点M的轨迹方程判断轨迹的形状.引申.引申.课堂练习1. P是双曲线 上任意一点,O为原点,则OP线段中点Q的轨迹方程是( ) B2.已知双曲线 右支上有一条过右焦点的弦AB,其长度为m,求A、B与左焦点构成的三角形的周长.3. 方程mx2-my2=n中mn<0,则其表示焦点在 轴上 的 .x 双曲线4. 若方程(k2+k-2)x2+(k+1)y2=1的曲线是焦点在y轴上的
双曲线,则k? .(-1, 1)5. 双曲线 的焦点坐标是 . 6. 双曲线 的焦距是6,则k= . ?6 7. 若方程 表示双曲线,求实数k的
取值范围. -25例4.已知F1、F2为双曲线 的焦点,弦
MN过F1且M,N在同一支上,若|MN|=7, 求△MF2N的
周长.例5.已知双曲线16x2-9y2=144
①求焦点的坐标;
②设P为双曲线上一点,且|PF1|?|PF2|=32,求 ;
③设P为双曲线上一点,且? F1PF2=120?,求 . 变式.已知双曲线 的左、右焦点分别为F1、F2,点M为双曲线上任意一点,并且∠F1MF2=θ,求ΔF1MF2的面积.想一想:这个三角形叫做什么三角形,椭圆中有无类似的问题.变形:角度改为其它特殊角呢?思考:求这个焦点三角形的面积?双曲线 的焦点三角形的面积为椭圆 的焦点三角形的面积为例6.1.用待定系数法求双曲线标准方程的步骤:2.用定义法求双曲线标准方程的注意事项:(1)定位:确定焦点位置,若不能确定,应分类讨论
定型:求a,b,c 的值.
(2)若过两点,无法判断焦点位置,这时可设为
AX2-BY2=1 (AB>0)何时为双曲线一支,何时为双曲线两支?小 结
标准方程① 两个定点F1、F2——双曲线的焦点;② |F1F2|=2c ——焦距.(1)2a<2c ; 平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于︱F1F2︱)的点的轨迹叫做双曲线.(2)2a >0 ;双曲线定义思考:(1)若2a=2c,则轨迹是什么?(2)若2a>2c,则轨迹是什么?说明(3)若2a=0,则轨迹是什么? | |MF1| - |MF2| | = 2a(1)两条射线(2)不表示任何轨迹(3)线段F1F2的垂直平分线F1F2yxoyoxF1F2|PF1—PF2|=2a(2a<|F1F2|)F1(-c,0),F2(c,0)F1(0,-c),F2(0,c)c2=a2+b2双曲线 使A、B两点在x轴上,并且点O与线段AB的中点重合解: 由声速及在A地听到炮弹爆炸声比在B地晚2s,可知A地与爆炸点的距离比B地与爆炸点的距离远680m.因为|AB|>680m,所以爆炸点的轨迹是以A、B为焦点的双曲线在靠近B处的一支上.例1.已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.建立直角坐标系xOy,设爆炸点P的坐标为(x,y),则即 2a=680,a=340因此炮弹爆炸点的轨迹方程为答:再增设一个观测点C,利用B、C(或A、C)两处测得的爆炸声的时间差,可以求出另一个双曲线的方程,解这两个方程组成的方程组,就能确定爆炸点的准确位置.这是双曲线的一个重要应用.其实全球定位系统就是根据例2这个原理来定位的解: 在△ABC中,|BC|=10,故顶点A的轨迹是以B、C为焦点的双曲线的左支又因c=5,a=3,则b=4则顶点A的轨迹方程为例3:根据下列条件,求双曲线的标准方程例4.如图,点A,B的坐标分别是(-5,0),(5,0),直线AM,BM相交于点M,且它们斜率之积是4/9,试求点M的轨迹方程,并由点M的轨迹方程判断轨迹的形状.引申.引申.课堂练习1. P是双曲线 上任意一点,O为原点,则OP线段中点Q的轨迹方程是( ) B2.已知双曲线 右支上有一条过右焦点的弦AB,其长度为m,求A、B与左焦点构成的三角形的周长.3. 方程mx2-my2=n中mn<0,则其表示焦点在 轴上 的 .x 双曲线4. 若方程(k2+k-2)x2+(k+1)y2=1的曲线是焦点在y轴上的
双曲线,则k? .(-1, 1)5. 双曲线 的焦点坐标是 . 6. 双曲线 的焦距是6,则k= . ?6 7. 若方程 表示双曲线,求实数k的
取值范围. -2
MN过F1且M,N在同一支上,若|MN|=7, 求△MF2N的
周长.例5.已知双曲线16x2-9y2=144
①求焦点的坐标;
②设P为双曲线上一点,且|PF1|?|PF2|=32,求 ;
③设P为双曲线上一点,且? F1PF2=120?,求 . 变式.已知双曲线 的左、右焦点分别为F1、F2,点M为双曲线上任意一点,并且∠F1MF2=θ,求ΔF1MF2的面积.想一想:这个三角形叫做什么三角形,椭圆中有无类似的问题.变形:角度改为其它特殊角呢?思考:求这个焦点三角形的面积?双曲线 的焦点三角形的面积为椭圆 的焦点三角形的面积为例6.1.用待定系数法求双曲线标准方程的步骤:2.用定义法求双曲线标准方程的注意事项:(1)定位:确定焦点位置,若不能确定,应分类讨论
定型:求a,b,c 的值.
(2)若过两点,无法判断焦点位置,这时可设为
AX2-BY2=1 (AB>0)何时为双曲线一支,何时为双曲线两支?小 结
