2022年人教版八年级数学 下册 19.2.2 一次函数 第2课时 用待定系数法求一次函数的解析式 课件(共42张)
文档属性
| 名称 | 2022年人教版八年级数学 下册 19.2.2 一次函数 第2课时 用待定系数法求一次函数的解析式 课件(共42张) |  | |
| 格式 | zip | ||
| 文件大小 | 484.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 19:07:33 | ||
图片预览





文档简介
(共28张PPT)
你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
思考:
反过来已知一个一次函数的图象经过两个具体的点,
你能求出它的解析式吗?
两点法——两点确定一条直线
导入新课
19.2.2 一次函数
人教版八年级数学 下册
第2课时 用待定系数法求一次函数的解析式
学习目标:
1.学会用待定系数法求一次函数解析式;
2.了解分段函数的表示及其图象;能初步应用一次函数模型解决现实生活中的问题。
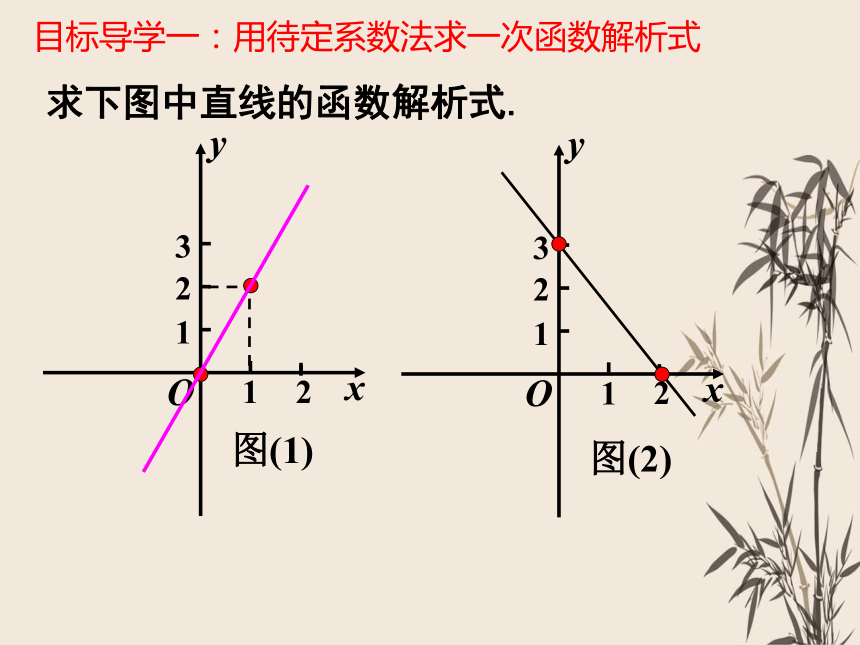
求下图中直线的函数解析式.
O
x
1
3
1
2
2
y
图(2)
O
x
1
3
1
2
2
y
图(1)
目标导学一:用待定系数法求一次函数解析式
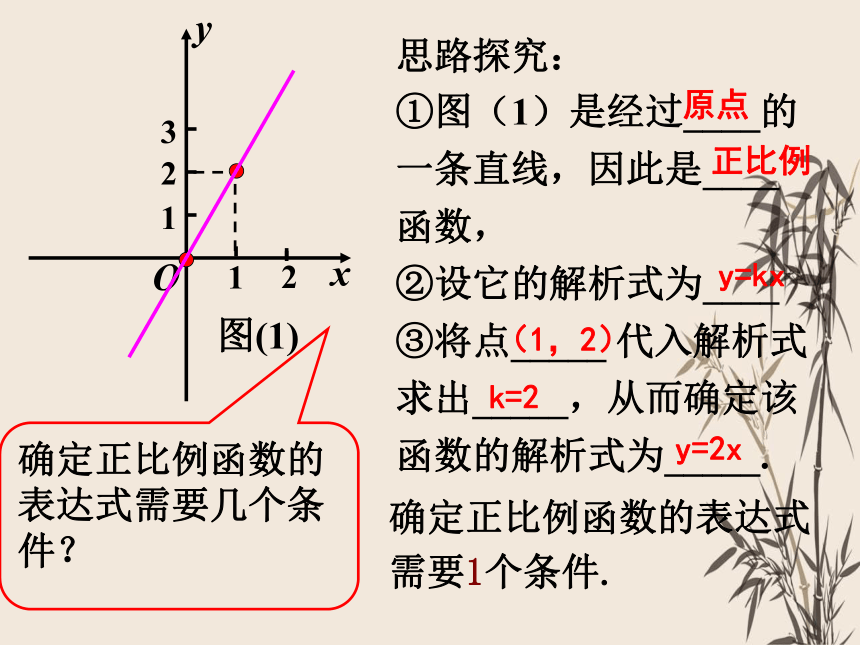
思路探究:
①图(1)是经过____的一条直线,因此是____ 函数,
②设它的解析式为____
③将点_____ 代入解析式求出_____,从而确定该函数的解析式为_____.
O
x
1
3
1
2
2
y
图(1)
(1,2)
y=2x
k=2
y=kx
正比例
原点
确定正比例函数的表达式需要几个条件?
确定正比例函数的表达式需要1个条件.
O
x
1
3
1
2
2
y
图(2)
思路探究:
图(2)设直线的解析式是________,因为此直线经过点______,_______,因此将这两个点的坐标代 入可得关于k,b方程组,从而确定k,b的值,确定了解析式。
y=kx+b
(0,3)
(2,0)
确定一次函数的表达式需要几个条件?
确定一次函数的表达式需要2个条件.
(2)设直线的解析式为y=kx+b.
∵经过点(2,0), (0,3),
解(1)设直线的解析式为y=kx.
∵经过点(1,2),
∴ k=2.
∴这条直线的解析式为y=2x.
∴
∴
∴这条直线的解析式为
小结:确定正比例函数的解析式需要一个条件,确定一次函数的解析式需要两个条件.
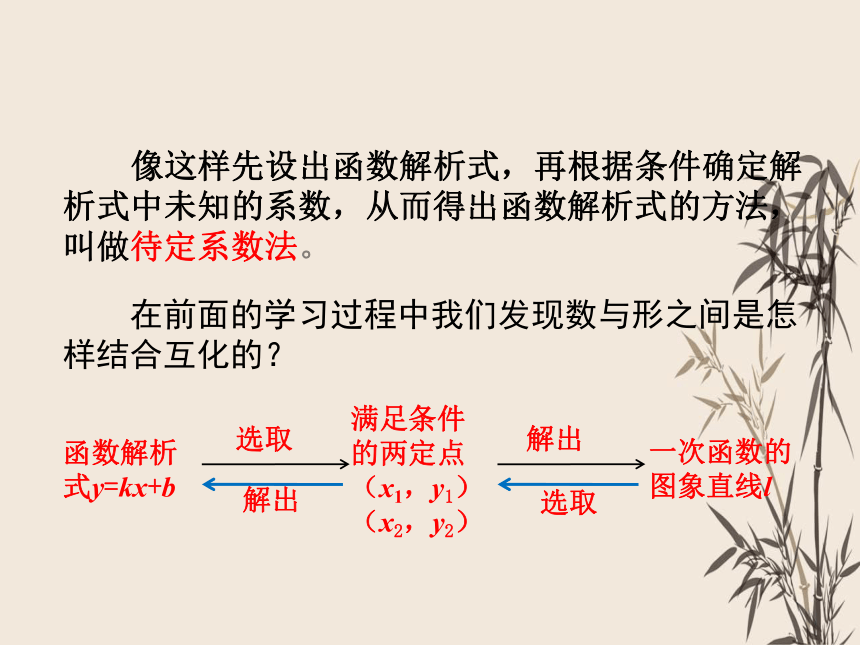
像这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法。
在前面的学习过程中我们发现数与形之间是怎样结合互化的?
函数解析式y=kx+b
一次函数的图象直线l
满足条件的两定点(x1,y1)(x2,y2)
解出
选取
选取
解出
(待定系数法)
满足条件的两 定点(x1,y1)与(x2,y2)
函数解析式
y =kx+b
一次函数的 图象直线l
选取
解出
画出
选取
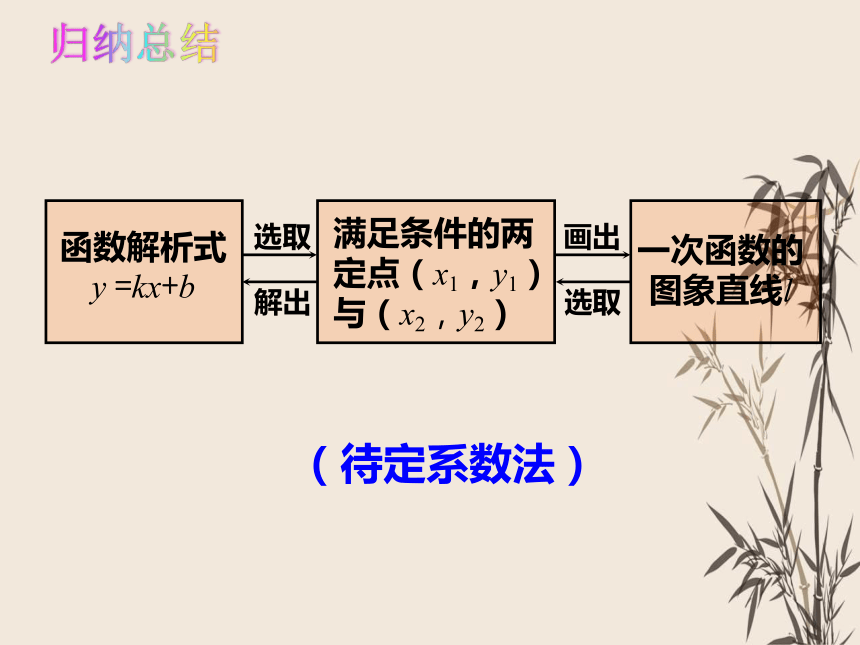
归纳总结
先设出函数解析式,
再根据条件确定解析式中未知系数,从而得出函数解析式的方法,
叫做待定系数法。
归纳总结
待定系数法:
例1 已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式.
分析:一次函数的图象过点(3,5)与(-4,-9),因此这两点的坐标适合一次函数
精典例题
解:设这个一次函数的解析式为
把点(3,5)与(-4,-9)分别代入,得
,
.
解方程组得 _____________
_____________
∴这个一次函数的解析式为___________.
y=2x-1
3k+b=5
-4k+b=-9
k=2
b=-1
(1)设一次函数的一般形式y=kx+b(k≠0) ;
(2)根据已知条件列出关于k 、b的二元一次方程组;
(3)解这个方程组,求出k、b ;
(4)将已经求出的 k、 b的值代入所设解析式.
待定系数法求一次函数解析式的步骤:
解:设这个一次函数的解析式为y=kx+b(k≠0)
把点(9,0)与(24,20)分别代入,得
解方程组得
∴这个一次函数的解析式为___________.
1.一次函数图象经过点(9,0)和点(24,20),写出函数解析式.
即学即练
2.若一次函数的图象经过点 A(2,0)且与直线y=-x+3平行,求其解析式.
解:设这个一次函数的解析式为y=kx+b.
k = -1,
2k + b = 0,
{
由题意得
k = -1,
b = 2.
{
解得
∴y=-x+2.
即学即练
购买种子 数量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
例2 “黄金1号”玉米种子的价格为5元/kg,如果
一次购买2kg以上的种子,超过2kg部分的种子的价格打8折。
(1)填出下表:
2.5
5
7.5
10
12
14
16
18
目标导学二:一次函数的图象的实际应用
例2 “黄金1号”玉米种子的价格为5元/kg,如果
一次购买2kg以上的种子,超过2kg部分的种子的价格打8折。
(2)写出付款金额 y(单位:元)与购买种子数量
x(单位:kg)之间的函数解析式,并画出函数图象。
设购买量为x kg,付款金额为y元。
当0≤x≤2时,y=5x;
当x>2时,y=4(x-2)+10=4x+2。
例3 A城有肥料200吨,B城有肥料300吨,现要把这些肥料全部运往C、D两乡。从A城往C、D两乡运肥料的费用分别为每吨20元和25元;从B城往C、D两乡运肥料的费用分别为每吨15元和24元,现C乡需要肥料240吨, D乡需要肥料260吨,怎样调运总运费最少?
解:设总运费为y元,A城运往C乡的肥料量
为x吨,那么A城运往D乡的肥料量为(200-x)
吨,B城运往C乡的肥料量为(240-x)吨, B城
运往D乡的肥料量为(60+x)吨.
由总运费与各运输量的关系可知,反映
y与x之间关系的函数为
y=20x+25(200-x)+15(240-x)+24(60+x)
y=4x+10040 (0≤x≤200)
化简得:
画y=4x+10040 (0≤x≤200)
列表:
描点:
连线:
x
y=4x
0
1
由解析式和图象可以看出:当x=0时,运费y有最小值10040.
A城→C乡0吨
A城→D乡200吨
B城→C乡240吨
B城→D乡60吨
精典例题
小明将父母给的零用钱按每月相等的数额存放在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数x(月)之间的关系如图所示,根据下图回答下列问题:
(1)求出y关于x的函数解析式。
(2)根据关系式计算,小明经过几个月才能存够200元?
O
40
x
y
1
2
3
120
80
4
y=20x+40
8个月
即学即练
设:设一次函数的解析式为y=kx+b(k≠0);
代:把图象上的点(x1,y1),(x2,y2)代入一次函
数的解析式,组成二元一次方程组;
求:求解二元一次方程组得k,b的值;
写(还原):把k,b的值代入一次函数的解析式.
待定系数法求一次函数解析式的步骤
一次函数与实际问题
课堂总结
1.若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过点( )
A (-1,1) B (2,2)
C (-2,2) D (2,一2)
检测目标
B
2.若直线y=kx+b平行于直线y=-3x+2,且在y轴上的的交点坐标为(0,-5),则k的值是( )
A 2 B 3 C 4 D 5
B
检测目标
3.若一次函数y=3x+b的图象经过点P(1,4),则
该函数图象的解析式为( )
A
检测目标
A y=3x+1
B y=4x+1
C y=x+1
D y=2x+1
4.某航空公司规定,旅客乘机所携带行李的质量x( kg )与其运费y( 元 )由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量( )
A
检测目标
A.20 kg B.25 kg
C.28 kg D.30 kg
5.为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示。
(1)根据图象,请分别求出当0≤x≤50和x>50时,y与x的函数解析式。
(2)请回答:
当每月用电量不超过50度时,收费标准是 ;
当每月用电量超过50度时,收费标准是 。
0.9元/度
0.5元/度
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
思考:
反过来已知一个一次函数的图象经过两个具体的点,
你能求出它的解析式吗?
两点法——两点确定一条直线
导入新课
19.2.2 一次函数
人教版八年级数学 下册
第2课时 用待定系数法求一次函数的解析式
学习目标:
1.学会用待定系数法求一次函数解析式;
2.了解分段函数的表示及其图象;能初步应用一次函数模型解决现实生活中的问题。
求下图中直线的函数解析式.
O
x
1
3
1
2
2
y
图(2)
O
x
1
3
1
2
2
y
图(1)
目标导学一:用待定系数法求一次函数解析式
思路探究:
①图(1)是经过____的一条直线,因此是____ 函数,
②设它的解析式为____
③将点_____ 代入解析式求出_____,从而确定该函数的解析式为_____.
O
x
1
3
1
2
2
y
图(1)
(1,2)
y=2x
k=2
y=kx
正比例
原点
确定正比例函数的表达式需要几个条件?
确定正比例函数的表达式需要1个条件.
O
x
1
3
1
2
2
y
图(2)
思路探究:
图(2)设直线的解析式是________,因为此直线经过点______,_______,因此将这两个点的坐标代 入可得关于k,b方程组,从而确定k,b的值,确定了解析式。
y=kx+b
(0,3)
(2,0)
确定一次函数的表达式需要几个条件?
确定一次函数的表达式需要2个条件.
(2)设直线的解析式为y=kx+b.
∵经过点(2,0), (0,3),
解(1)设直线的解析式为y=kx.
∵经过点(1,2),
∴ k=2.
∴这条直线的解析式为y=2x.
∴
∴
∴这条直线的解析式为
小结:确定正比例函数的解析式需要一个条件,确定一次函数的解析式需要两个条件.
像这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法。
在前面的学习过程中我们发现数与形之间是怎样结合互化的?
函数解析式y=kx+b
一次函数的图象直线l
满足条件的两定点(x1,y1)(x2,y2)
解出
选取
选取
解出
(待定系数法)
满足条件的两 定点(x1,y1)与(x2,y2)
函数解析式
y =kx+b
一次函数的 图象直线l
选取
解出
画出
选取
归纳总结
先设出函数解析式,
再根据条件确定解析式中未知系数,从而得出函数解析式的方法,
叫做待定系数法。
归纳总结
待定系数法:
例1 已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式.
分析:一次函数的图象过点(3,5)与(-4,-9),因此这两点的坐标适合一次函数
精典例题
解:设这个一次函数的解析式为
把点(3,5)与(-4,-9)分别代入,得
,
.
解方程组得 _____________
_____________
∴这个一次函数的解析式为___________.
y=2x-1
3k+b=5
-4k+b=-9
k=2
b=-1
(1)设一次函数的一般形式y=kx+b(k≠0) ;
(2)根据已知条件列出关于k 、b的二元一次方程组;
(3)解这个方程组,求出k、b ;
(4)将已经求出的 k、 b的值代入所设解析式.
待定系数法求一次函数解析式的步骤:
解:设这个一次函数的解析式为y=kx+b(k≠0)
把点(9,0)与(24,20)分别代入,得
解方程组得
∴这个一次函数的解析式为___________.
1.一次函数图象经过点(9,0)和点(24,20),写出函数解析式.
即学即练
2.若一次函数的图象经过点 A(2,0)且与直线y=-x+3平行,求其解析式.
解:设这个一次函数的解析式为y=kx+b.
k = -1,
2k + b = 0,
{
由题意得
k = -1,
b = 2.
{
解得
∴y=-x+2.
即学即练
购买种子 数量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
例2 “黄金1号”玉米种子的价格为5元/kg,如果
一次购买2kg以上的种子,超过2kg部分的种子的价格打8折。
(1)填出下表:
2.5
5
7.5
10
12
14
16
18
目标导学二:一次函数的图象的实际应用
例2 “黄金1号”玉米种子的价格为5元/kg,如果
一次购买2kg以上的种子,超过2kg部分的种子的价格打8折。
(2)写出付款金额 y(单位:元)与购买种子数量
x(单位:kg)之间的函数解析式,并画出函数图象。
设购买量为x kg,付款金额为y元。
当0≤x≤2时,y=5x;
当x>2时,y=4(x-2)+10=4x+2。
例3 A城有肥料200吨,B城有肥料300吨,现要把这些肥料全部运往C、D两乡。从A城往C、D两乡运肥料的费用分别为每吨20元和25元;从B城往C、D两乡运肥料的费用分别为每吨15元和24元,现C乡需要肥料240吨, D乡需要肥料260吨,怎样调运总运费最少?
解:设总运费为y元,A城运往C乡的肥料量
为x吨,那么A城运往D乡的肥料量为(200-x)
吨,B城运往C乡的肥料量为(240-x)吨, B城
运往D乡的肥料量为(60+x)吨.
由总运费与各运输量的关系可知,反映
y与x之间关系的函数为
y=20x+25(200-x)+15(240-x)+24(60+x)
y=4x+10040 (0≤x≤200)
化简得:
画y=4x+10040 (0≤x≤200)
列表:
描点:
连线:
x
y=4x
0
1
由解析式和图象可以看出:当x=0时,运费y有最小值10040.
A城→C乡0吨
A城→D乡200吨
B城→C乡240吨
B城→D乡60吨
精典例题
小明将父母给的零用钱按每月相等的数额存放在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数x(月)之间的关系如图所示,根据下图回答下列问题:
(1)求出y关于x的函数解析式。
(2)根据关系式计算,小明经过几个月才能存够200元?
O
40
x
y
1
2
3
120
80
4
y=20x+40
8个月
即学即练
设:设一次函数的解析式为y=kx+b(k≠0);
代:把图象上的点(x1,y1),(x2,y2)代入一次函
数的解析式,组成二元一次方程组;
求:求解二元一次方程组得k,b的值;
写(还原):把k,b的值代入一次函数的解析式.
待定系数法求一次函数解析式的步骤
一次函数与实际问题
课堂总结
1.若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过点( )
A (-1,1) B (2,2)
C (-2,2) D (2,一2)
检测目标
B
2.若直线y=kx+b平行于直线y=-3x+2,且在y轴上的的交点坐标为(0,-5),则k的值是( )
A 2 B 3 C 4 D 5
B
检测目标
3.若一次函数y=3x+b的图象经过点P(1,4),则
该函数图象的解析式为( )
A
检测目标
A y=3x+1
B y=4x+1
C y=x+1
D y=2x+1
4.某航空公司规定,旅客乘机所携带行李的质量x( kg )与其运费y( 元 )由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量( )
A
检测目标
A.20 kg B.25 kg
C.28 kg D.30 kg
5.为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示。
(1)根据图象,请分别求出当0≤x≤50和x>50时,y与x的函数解析式。
(2)请回答:
当每月用电量不超过50度时,收费标准是 ;
当每月用电量超过50度时,收费标准是 。
0.9元/度
0.5元/度
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
