2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册5.3.1函数的单调性(3)(普宁华美5步法)(共16张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册5.3.1函数的单调性(3)(普宁华美5步法)(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 21:14:55 | ||
图片预览





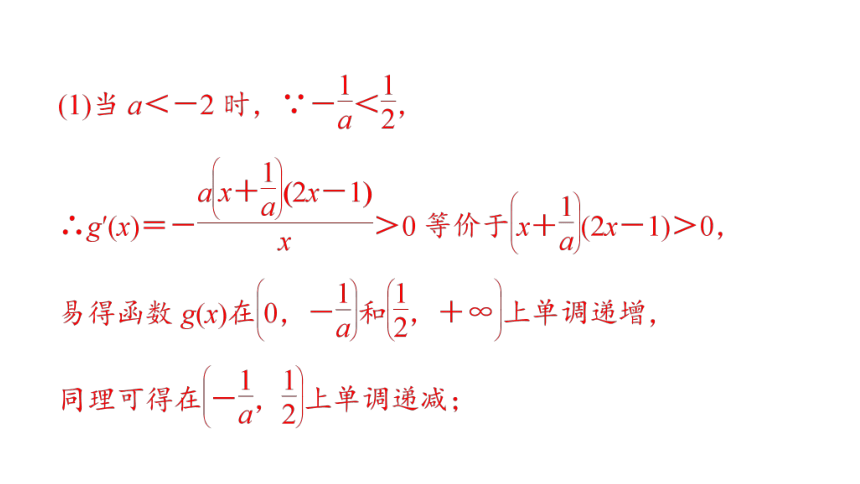

文档简介
(共16张PPT)
高二数学选择性必修第二册
第五章 一元函数的导数及其应
5.3.1 函数的单调性(三)
学习目标
1.掌握利用导数判断函数的单调性的一般步骤.
2. 学会处理含参函数的单调性问题
一、学习目标(1分钟)
定义域
零点
零点
正负
二、问题导学(3分钟)
当堂达标
三、点拨精讲(28分钟)
例
典例解析
三、点拨精讲(28分钟)
2
归纳总结
例3
利用导数法解决取值范围问题的两个基本思路
①将问题转化为不等式在某区间上的恒成立问题,即f′(x)≥0(或f′(x)≤0)恒成立,利用分离参数或函数性质求解参数范围,然后检验参数取“=”时是否满足题意.
②先令f′(x)>0(或f′(x)<0),求出参数的取值范围后,再验证参数取“=”时f(x)是否满足题意.
(2)理清运算对象,选择运算方法,求得运算结果,充分体现数学运算的数学核心素养.
1、
四、课堂小结(1分钟)
2、利用导数法解决取值范围问题
跟踪训练
五、当堂检测(12分钟)
2.若函数 f (x)= kx-ln x 在区间 (1,+∞) 上单调递增,
则 k 的取值范围是________.
[ 1 , +∞ )
解:∵ f (x)=kx-lnx,
∴ f ' (x) = k- ,
又函数 f (x) 在区间 (1, +∞) 上单调递增,
∴ f ' (x) ≥ 0 在 (1, +∞)上恒成立,即 k- ≥ 0,
k ≥ ,∵ x∈(1, +∞),∴ ∈ (0, 1),
∴ k ≥ 1.
1
x
1
x
1
x
1
x
高二数学选择性必修第二册
第五章 一元函数的导数及其应
5.3.1 函数的单调性(三)
学习目标
1.掌握利用导数判断函数的单调性的一般步骤.
2. 学会处理含参函数的单调性问题
一、学习目标(1分钟)
定义域
零点
零点
正负
二、问题导学(3分钟)
当堂达标
三、点拨精讲(28分钟)
例
典例解析
三、点拨精讲(28分钟)
2
归纳总结
例3
利用导数法解决取值范围问题的两个基本思路
①将问题转化为不等式在某区间上的恒成立问题,即f′(x)≥0(或f′(x)≤0)恒成立,利用分离参数或函数性质求解参数范围,然后检验参数取“=”时是否满足题意.
②先令f′(x)>0(或f′(x)<0),求出参数的取值范围后,再验证参数取“=”时f(x)是否满足题意.
(2)理清运算对象,选择运算方法,求得运算结果,充分体现数学运算的数学核心素养.
1、
四、课堂小结(1分钟)
2、利用导数法解决取值范围问题
跟踪训练
五、当堂检测(12分钟)
2.若函数 f (x)= kx-ln x 在区间 (1,+∞) 上单调递增,
则 k 的取值范围是________.
[ 1 , +∞ )
解:∵ f (x)=kx-lnx,
∴ f ' (x) = k- ,
又函数 f (x) 在区间 (1, +∞) 上单调递增,
∴ f ' (x) ≥ 0 在 (1, +∞)上恒成立,即 k- ≥ 0,
k ≥ ,∵ x∈(1, +∞),∴ ∈ (0, 1),
∴ k ≥ 1.
1
x
1
x
1
x
1
x
