4.1 认识三角形 教学课件(共34张PPT)
文档属性
| 名称 | 4.1 认识三角形 教学课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-22 10:26:23 | ||
图片预览




文档简介
(共34张PPT)
认识三角形
北师大版 七年级上
新知导入
生活中的三角形
新知导入
生活中的三角形
百慕大三角
新知导入
生活中的三角形
夏季大三角
新知讲解
三角形概念
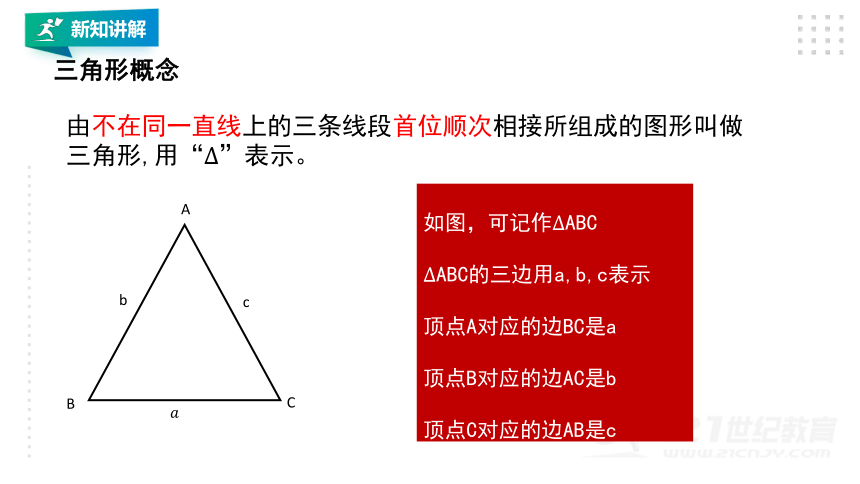
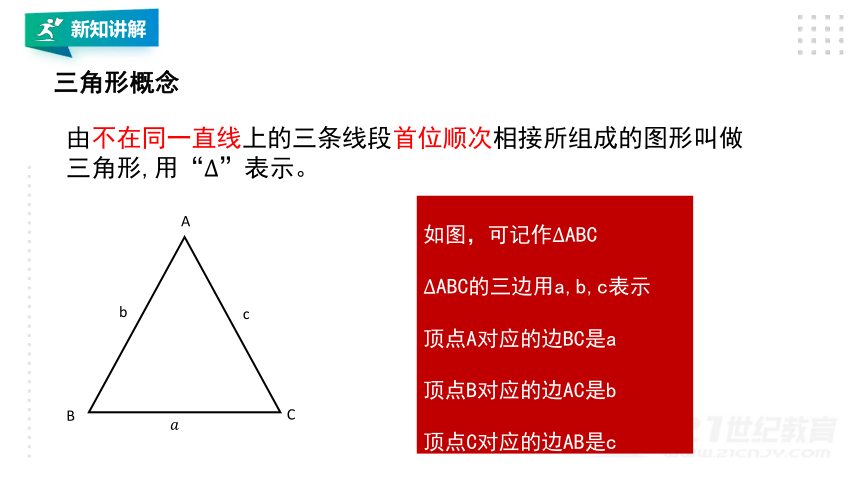
由不在同一直线上的三条线段首位顺次相接所组成的图形叫做三角形,用“”表示。
A
B
C
b
c
如图,可记ABC
ABC的三边用a,b,c表示
顶点A对应的边BC是a
顶点B对应的边AC是b
顶点C对应的边AB是c
新知讲解
三角形概念
由不在同一直线上的三条线段首位顺次相接所组成的图形叫做三角形,用“”表示。
A
B
C
b
c
如图,可记ABC
ABC的三边用a,b,c表示
顶点A对应的边BC是a
顶点B对应的边AC是b
顶点C对应的边AB是c
新知讲解
三角形概念
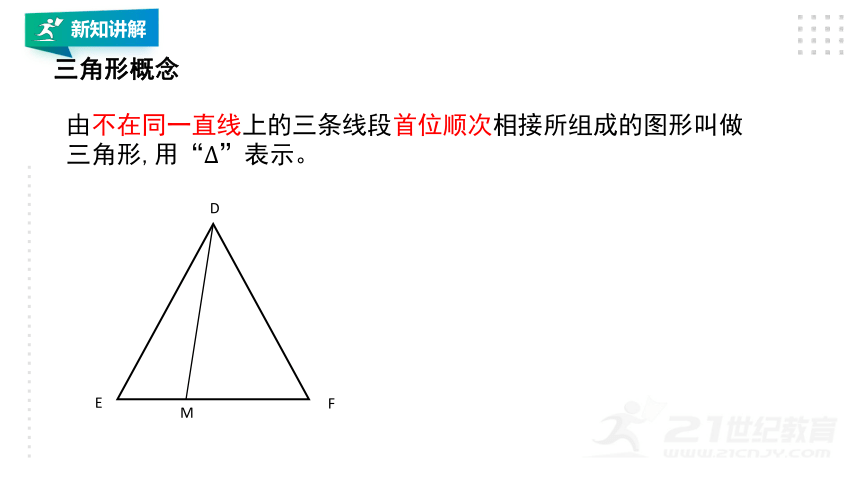
由不在同一直线上的三条线段首位顺次相接所组成的图形叫做三角形,用“”表示。
D
E
M
F
新知讲解
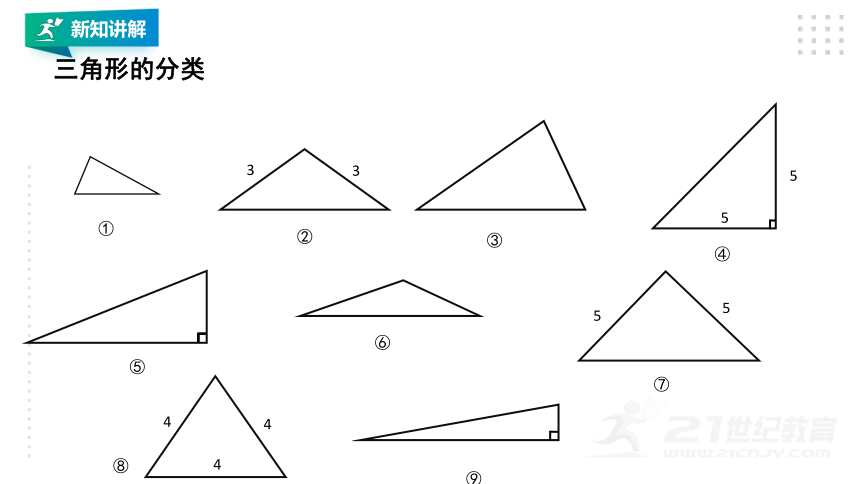
三角形的分类
①
④
②
⑥
⑤
⑦
⑨
⑧
③
3
5
3
4
4
4
5
5
5
新知讲解
三角形的分类
操作提示:
(1)用自己喜欢的一种方法给三角形进行分类。
(2)交流:每类三角形都有什么特点?
(3)试着给每类三角形起个名字。
新知讲解
三角形的分类
三个角都是锐角 锐角三角形。
有一个角是直角 直角三角形。
有一个角是钝角 钝角三角形。
按角分
按边分
3条边都相等
3条边都不相等
有2条边相等
等腰三角形
等边三角形/正三角形
不等边三角形
新知讲解
三角形的分类
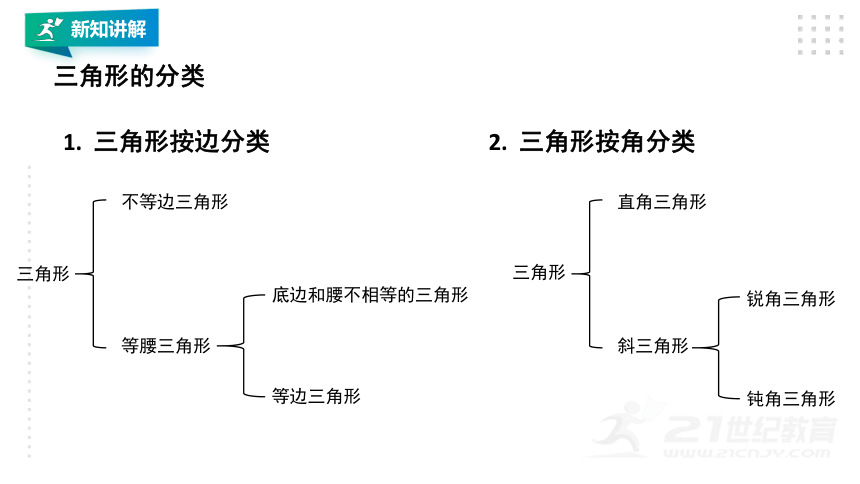
1. 三角形按边分类
2. 三角形按角分类
三角形
不等边三角形
等腰三角形
底边和腰不相等的三角形
等边三角形
三角形
直角三角形
斜三角形
锐角三角形
钝角三角形
新知讲解
小试牛刀
1. 三角形是( )
连接任意三点组成的图形.
由不在同一条直线上的三条线段首位顺次相接所成的图形.
由三条线段组成的图形.
以上说法均不对.
新知讲解
小试牛刀
2. 试通过画图来判定,下列说法正确的是( )
一个直角三角形一定不是等腰三角形.
一个等腰三角形一定不是锐角三角形.
一个钝角三角形一定不是等腰三角形.
一个等边三角形一定不是钝角三角形.
新知讲解
小试牛刀
3. 三角形按边可分为( )
等腰三角形,直角三角形,锐角三角形.
直角三角形,不等边三角形.
等腰三角形,不等边三角形.
等腰三角形,等边三角形.
新知讲解
三角形的内角和
如何证明三角形内角和等于180°?
量,剪,拼
还有其它方法吗?
定义:三角形两边的夹角叫做三角形的内角
新知讲解
三角形的内角和
如何证明三角形内角和等于180°?
1
3
2
4
证:过A点作直线∥BC
A
B
C
m
5
∵ ∥BC
∴∠1=∠3,∠2=∠4(两直线平行,内错角相等)
又∵∠3+∠4+∠5=180°
∴∠1+∠2+∠5=180°
还有其它证明方法吗?
新知讲解
三角形的内角和
如何证明三角形内角和等于180°?
定义:三角形两边的夹角叫做三角形的内角
定理:三角形的内角和等于180°
为了证明三个角的和为1800,通过画图,转化为一个平角或同旁内角互补,转化思想是常用的数学思想。
推论:直角三角形的两个锐角互余
新知讲解
三角形的外角和
定义:三角形的一条边与另一条边的延长线组成的角,叫做三角形的外角。
三角形有6个外角
定理:三角形外角和等于360°
新知讲解
小试牛刀
4. (口答)下列各组角是同一个三角形的内角吗 为什么
(3)90°, 10°, 90°
(6)50°, 50°, 50°
(1)3°, 150°, 27°
(不 是)
(2)3°, 150°, 100°
(4)90°, 40°, 50°
(5)60°, 60°,60°
( 是 )
(不 是)
( 是 )
( 是 )
(不 是)
新知讲解
小试牛刀
( 2 ) 在△ABC中, ∠A=40 °, ∠A=2∠B,则∠C = ____。
( 1 )在△ABC中,∠A=35°,∠ B=43 °,则∠C = ____
( 3 ) 在△ABC中,∠A:∠B:∠C=1:2:3,求∠A = ____,
∠B = ____,∠C = ____。
5. 计算下列角的度数
新知讲解
三角形的三边关系
1m 2m 3m 4m
新知讲解
三角形三边关系
A
B
C
1. 三角形的任意两边之和大于第三边
AB+AC>BC
2. 三角形的任意两边之差小于第三边
BCAC<AB
新知讲解
小试牛刀
6.在下列长度的四根木棒中,能与4cm、9cm长的两根木棒钉成一个三角形的是( ).
A.4cm B.5cm C.9cm D.13cm
7. 三角形的一边为5 cm,一边为7 cm,则第三边的取值范围是____
8. 已知△ABC为等腰三角形,①当它的两个边长分别为8 cm和3 cm时,它的周长为_____;②如果它的一边长为4cm,一边的长为6cm,则周长为_____.
新知讲解
三角形中的重要线段
1. 三角形的高
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高线,叫做三角形的高。
A
B
C
F
新知讲解
三角形中的重要线段
1. 三角形的高
A
B
C
E
F
G
A
B
C
D
A
B
C
E
D
F
新知讲解
三角形中的重要线段
①锐角三角形、直角三角形、钝角三角形都有高线,三角形的三条高线所在 直线相交与一点。
②锐角三角形的高线交于三角形的内部一点。直角三角形高线交于直角顶点。钝角三角形高线交于三角形外部一点。
③三角形的高是线段,而垂线是直线。
1. 三角形的高
新知讲解
小试牛刀
9. 下列各个图形中,哪一个图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
D
新知讲解
三角形中的重要线段
2. 三角形的中线
A
B
C
D
如左图,连接△ABC的顶点和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线。
定义:在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线。
.
什么是三角形的中线
新知讲解
三角形中的重要线段
总结:三角形的任意一条中线把这个三角形分成了两个面积相等的三角形。
E
A
B
C
D
如右图
∵D是BC的中点
∴BD=DC
而△ABD的面积= BD×AE
△ADC的面积= DC×AE
故△ABD的面积= △ADC的面积
2. 三角形的中线
新知讲解
三角形中的重要线段
2. 三角形的中线
①任何三角形有三条中线,并且都在三角形的内部,交于一点。
②三角形的中线是一条线段。
③三角形的任意一条中线把这个三角形分成了两个面积相等的三角形。
请同学们自己任意画一个三角形,然后画出它的中线。
想一想可以画几条?他们有什么特点?
课堂练习
2. 三角形的中线
10. 如图有一块三角形的菜地,现在要求分成面积比为2:3:4三块,且图中A处是三块菜地的共同的水源处。问:怎样分?
A
·
·
2
3
4
B
C
课堂练习
三角形中的重要线段
3. 三角形的加平分线
A
C
B
F
E
D
O
∵BE是△ABC的角平分线
∴____ =_____ = _____
∴∠ACB=2______=2______
∠ABE
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线
∠BCF
https://www.21cnjy.com/help/help_extract.php
认识三角形
北师大版 七年级上
新知导入
生活中的三角形
新知导入
生活中的三角形
百慕大三角
新知导入
生活中的三角形
夏季大三角
新知讲解
三角形概念
由不在同一直线上的三条线段首位顺次相接所组成的图形叫做三角形,用“”表示。
A
B
C
b
c
如图,可记ABC
ABC的三边用a,b,c表示
顶点A对应的边BC是a
顶点B对应的边AC是b
顶点C对应的边AB是c
新知讲解
三角形概念
由不在同一直线上的三条线段首位顺次相接所组成的图形叫做三角形,用“”表示。
A
B
C
b
c
如图,可记ABC
ABC的三边用a,b,c表示
顶点A对应的边BC是a
顶点B对应的边AC是b
顶点C对应的边AB是c
新知讲解
三角形概念
由不在同一直线上的三条线段首位顺次相接所组成的图形叫做三角形,用“”表示。
D
E
M
F
新知讲解
三角形的分类
①
④
②
⑥
⑤
⑦
⑨
⑧
③
3
5
3
4
4
4
5
5
5
新知讲解
三角形的分类
操作提示:
(1)用自己喜欢的一种方法给三角形进行分类。
(2)交流:每类三角形都有什么特点?
(3)试着给每类三角形起个名字。
新知讲解
三角形的分类
三个角都是锐角 锐角三角形。
有一个角是直角 直角三角形。
有一个角是钝角 钝角三角形。
按角分
按边分
3条边都相等
3条边都不相等
有2条边相等
等腰三角形
等边三角形/正三角形
不等边三角形
新知讲解
三角形的分类
1. 三角形按边分类
2. 三角形按角分类
三角形
不等边三角形
等腰三角形
底边和腰不相等的三角形
等边三角形
三角形
直角三角形
斜三角形
锐角三角形
钝角三角形
新知讲解
小试牛刀
1. 三角形是( )
连接任意三点组成的图形.
由不在同一条直线上的三条线段首位顺次相接所成的图形.
由三条线段组成的图形.
以上说法均不对.
新知讲解
小试牛刀
2. 试通过画图来判定,下列说法正确的是( )
一个直角三角形一定不是等腰三角形.
一个等腰三角形一定不是锐角三角形.
一个钝角三角形一定不是等腰三角形.
一个等边三角形一定不是钝角三角形.
新知讲解
小试牛刀
3. 三角形按边可分为( )
等腰三角形,直角三角形,锐角三角形.
直角三角形,不等边三角形.
等腰三角形,不等边三角形.
等腰三角形,等边三角形.
新知讲解
三角形的内角和
如何证明三角形内角和等于180°?
量,剪,拼
还有其它方法吗?
定义:三角形两边的夹角叫做三角形的内角
新知讲解
三角形的内角和
如何证明三角形内角和等于180°?
1
3
2
4
证:过A点作直线∥BC
A
B
C
m
5
∵ ∥BC
∴∠1=∠3,∠2=∠4(两直线平行,内错角相等)
又∵∠3+∠4+∠5=180°
∴∠1+∠2+∠5=180°
还有其它证明方法吗?
新知讲解
三角形的内角和
如何证明三角形内角和等于180°?
定义:三角形两边的夹角叫做三角形的内角
定理:三角形的内角和等于180°
为了证明三个角的和为1800,通过画图,转化为一个平角或同旁内角互补,转化思想是常用的数学思想。
推论:直角三角形的两个锐角互余
新知讲解
三角形的外角和
定义:三角形的一条边与另一条边的延长线组成的角,叫做三角形的外角。
三角形有6个外角
定理:三角形外角和等于360°
新知讲解
小试牛刀
4. (口答)下列各组角是同一个三角形的内角吗 为什么
(3)90°, 10°, 90°
(6)50°, 50°, 50°
(1)3°, 150°, 27°
(不 是)
(2)3°, 150°, 100°
(4)90°, 40°, 50°
(5)60°, 60°,60°
( 是 )
(不 是)
( 是 )
( 是 )
(不 是)
新知讲解
小试牛刀
( 2 ) 在△ABC中, ∠A=40 °, ∠A=2∠B,则∠C = ____。
( 1 )在△ABC中,∠A=35°,∠ B=43 °,则∠C = ____
( 3 ) 在△ABC中,∠A:∠B:∠C=1:2:3,求∠A = ____,
∠B = ____,∠C = ____。
5. 计算下列角的度数
新知讲解
三角形的三边关系
1m 2m 3m 4m
新知讲解
三角形三边关系
A
B
C
1. 三角形的任意两边之和大于第三边
AB+AC>BC
2. 三角形的任意两边之差小于第三边
BCAC<AB
新知讲解
小试牛刀
6.在下列长度的四根木棒中,能与4cm、9cm长的两根木棒钉成一个三角形的是( ).
A.4cm B.5cm C.9cm D.13cm
7. 三角形的一边为5 cm,一边为7 cm,则第三边的取值范围是____
8. 已知△ABC为等腰三角形,①当它的两个边长分别为8 cm和3 cm时,它的周长为_____;②如果它的一边长为4cm,一边的长为6cm,则周长为_____.
新知讲解
三角形中的重要线段
1. 三角形的高
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高线,叫做三角形的高。
A
B
C
F
新知讲解
三角形中的重要线段
1. 三角形的高
A
B
C
E
F
G
A
B
C
D
A
B
C
E
D
F
新知讲解
三角形中的重要线段
①锐角三角形、直角三角形、钝角三角形都有高线,三角形的三条高线所在 直线相交与一点。
②锐角三角形的高线交于三角形的内部一点。直角三角形高线交于直角顶点。钝角三角形高线交于三角形外部一点。
③三角形的高是线段,而垂线是直线。
1. 三角形的高
新知讲解
小试牛刀
9. 下列各个图形中,哪一个图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
D
新知讲解
三角形中的重要线段
2. 三角形的中线
A
B
C
D
如左图,连接△ABC的顶点和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线。
定义:在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线。
.
什么是三角形的中线
新知讲解
三角形中的重要线段
总结:三角形的任意一条中线把这个三角形分成了两个面积相等的三角形。
E
A
B
C
D
如右图
∵D是BC的中点
∴BD=DC
而△ABD的面积= BD×AE
△ADC的面积= DC×AE
故△ABD的面积= △ADC的面积
2. 三角形的中线
新知讲解
三角形中的重要线段
2. 三角形的中线
①任何三角形有三条中线,并且都在三角形的内部,交于一点。
②三角形的中线是一条线段。
③三角形的任意一条中线把这个三角形分成了两个面积相等的三角形。
请同学们自己任意画一个三角形,然后画出它的中线。
想一想可以画几条?他们有什么特点?
课堂练习
2. 三角形的中线
10. 如图有一块三角形的菜地,现在要求分成面积比为2:3:4三块,且图中A处是三块菜地的共同的水源处。问:怎样分?
A
·
·
2
3
4
B
C
课堂练习
三角形中的重要线段
3. 三角形的加平分线
A
C
B
F
E
D
O
∵BE是△ABC的角平分线
∴____ =_____ = _____
∴∠ACB=2______=2______
∠ABE
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线
∠BCF
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
