人教版 数学五年级下册 长方体和正方体体积问题 课件(共19张PPT)
文档属性
| 名称 | 人教版 数学五年级下册 长方体和正方体体积问题 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-21 19:08:39 | ||
图片预览



文档简介
(共19张PPT)
长
方
和
正
体
方
体
体
积
什么是体积?
物体所占空间的大小叫做物体的体积。
立方厘米、立方分米和立方米,可以分别写
成cm 、dm 和m 。
常用的体积单位有哪些?
体积单位之间的进率是多少?
1立方米=1000立方分米
1立方分米=1000立方厘米
字母表示为:
1m =1000dm
1dm =1000cm
每相邻两个体积单位之间的进率为1000.
1cm
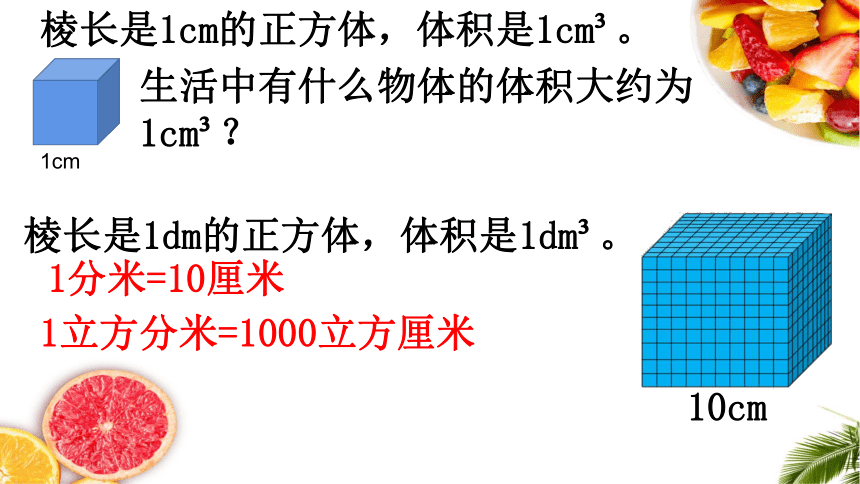
棱长是1cm的正方体,体积是1cm 。
10cm
棱长是1dm的正方体,体积是1dm 。
1立方分米=1000立方厘米
生活中有什么物体的体积大约为1cm ?
1分米=10厘米
10dm
棱长是1m的正方体,体积是1m 。
1立方米=1000立方分米
按照前面的方法想一想,1立方米等于多少立方分米?
1米=10分米
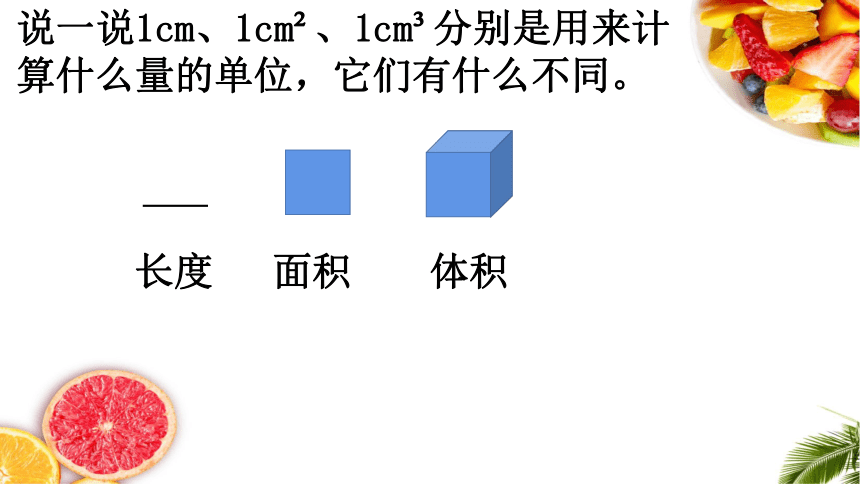
说一说1cm、1cm 、1cm 分别是用来计算什么量的单位,它们有什么不同。
长度
面积
体积
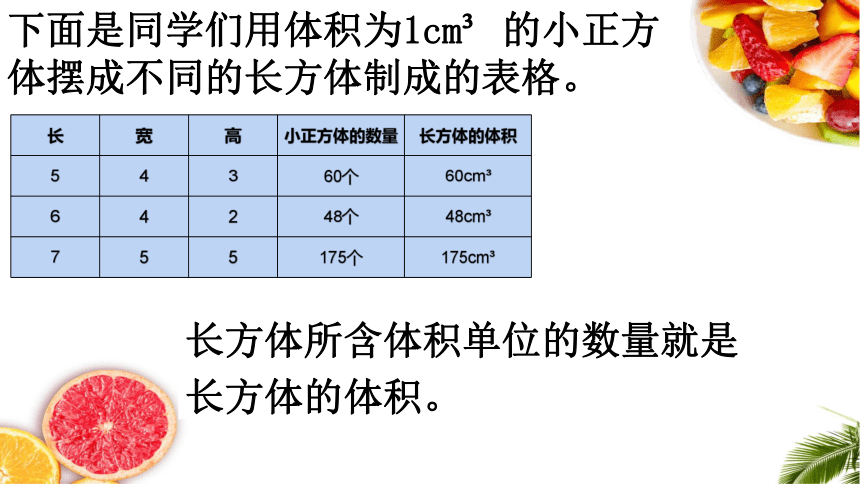
长方体所含体积单位的数量就是长方体的体积。
长 宽 高 小正方体的数量 长方体的体积
5 4 3 60个 60cm
6 4 2 48个 48cm
7 5 5 175个 175cm
下面是同学们用体积为1cm 的小正方体摆成不同的长方体制成的表格。
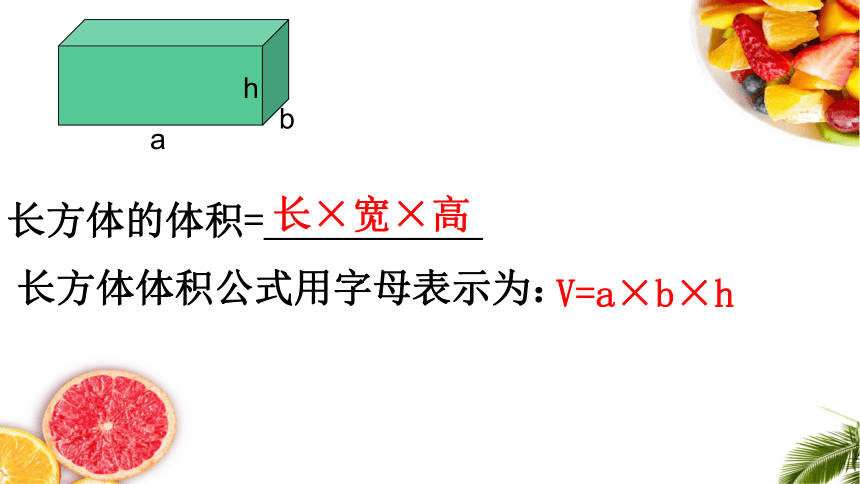
长方体的体积=___________
长×宽×高
a
b
h
长方体体积公式用字母表示为:
V=a×b×h
a
a
a
正方体的体积=__________________
棱长×棱长×棱长
正方体体积公式用字母表示为:
V=a×a×a
正方体的体积公式一般写成 :V=a
正方体是特殊的长方体
物体底面的面积叫做底面积。
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
底面积
底面积
所以长方体(或正方体)的体积=底面积×高
用字母S表示底面积时,V=S h
1、计算下面图形的体积
8cm
8cm
8cm
12cm
4cm
6cm
V=a
V=a b h
=8
=8×8×8
=512(cm )
=12×4×6
=288(cm )
2、世博钟楼位于上海火车站南广场中心位置,钟楼主体是长方体,长、宽约2.4米,高约15米,它的体积大约是多少?
V=a b h
=2.4×2.4×15
=86.4(立方米)
答:它的体积是86.4立方米。
3、一堆砖摆成长方体形状,长4米,宽20分米,高23分米,如果每立方米有500块砖,这堆砖共有多少块?
答:这堆砖共有9200块。
20分米=2米
23分米=2.3米
4×2×2.3=18.4(m )
18.4×500=9200(块)
4、学校运来7.6平方米的沙子,铺在一个长5米、宽38分米的沙坑里,可以铺多厚?
38分米=3.8米
S=5×3.8=19(平方米)
h=V÷S=7.6÷19=0.4(米)
答:可以铺0.4米厚。
5、一个游泳池长50米,宽21米,深2.5米。如果给游泳池注入2米深的水,每小时注入150立方米,几小时能注入完?
V=a b h
=50×21×2
=2100(立方米)
2100÷150=14(小时)
答:14小时能注入完。
6、把一个棱长8厘米的正方体钢块,锻造成长16厘米,宽5厘米的长方体钢板,这钢板厚多少厘米?
V=a
=8×8×8=512(立方厘米)
S=16×5=80(平方厘米)
答:这钢板厚6.4厘米。
h=V÷S=512÷80=6.4(厘米)
7、一段长为20分米的长方体木料,将它截成5段后,表面积增加40平方分米。这根木料原来的体积是多少?
(5-1)×2=8(个)
40÷8=5(平方分米)
答:这根木料原来的体积是100立方分米。
V=S h=5×20=100(立方分米)
8、一个长方体,如果长增加2cm,则体积增加40cm ;如果宽增加3cm,则体积增加90cm ;如果高增加4cm,则体积增加96cm 。求原长方体的表面积。
40÷2=20(cm )
90÷3=30(cm )
96÷4=24(cm )
(20+30+24)×2=148(cm )
答:原长方体的表面积为148平方厘米。
9、—个长方体木块,从下部和上部分别截去高为3cm和2cm的长方体后,便成为一个正方体,其表面积减少了120cm 。原来长方体的体积是多少立方厘米
120÷4÷(2+3)=6(cm)
6×6×(6+3+2)=396(cm )
答:原长方体的体积是396立方厘米。
感
谢
聆
听
长
方
和
正
体
方
体
体
积
什么是体积?
物体所占空间的大小叫做物体的体积。
立方厘米、立方分米和立方米,可以分别写
成cm 、dm 和m 。
常用的体积单位有哪些?
体积单位之间的进率是多少?
1立方米=1000立方分米
1立方分米=1000立方厘米
字母表示为:
1m =1000dm
1dm =1000cm
每相邻两个体积单位之间的进率为1000.
1cm
棱长是1cm的正方体,体积是1cm 。
10cm
棱长是1dm的正方体,体积是1dm 。
1立方分米=1000立方厘米
生活中有什么物体的体积大约为1cm ?
1分米=10厘米
10dm
棱长是1m的正方体,体积是1m 。
1立方米=1000立方分米
按照前面的方法想一想,1立方米等于多少立方分米?
1米=10分米
说一说1cm、1cm 、1cm 分别是用来计算什么量的单位,它们有什么不同。
长度
面积
体积
长方体所含体积单位的数量就是长方体的体积。
长 宽 高 小正方体的数量 长方体的体积
5 4 3 60个 60cm
6 4 2 48个 48cm
7 5 5 175个 175cm
下面是同学们用体积为1cm 的小正方体摆成不同的长方体制成的表格。
长方体的体积=___________
长×宽×高
a
b
h
长方体体积公式用字母表示为:
V=a×b×h
a
a
a
正方体的体积=__________________
棱长×棱长×棱长
正方体体积公式用字母表示为:
V=a×a×a
正方体的体积公式一般写成 :V=a
正方体是特殊的长方体
物体底面的面积叫做底面积。
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
底面积
底面积
所以长方体(或正方体)的体积=底面积×高
用字母S表示底面积时,V=S h
1、计算下面图形的体积
8cm
8cm
8cm
12cm
4cm
6cm
V=a
V=a b h
=8
=8×8×8
=512(cm )
=12×4×6
=288(cm )
2、世博钟楼位于上海火车站南广场中心位置,钟楼主体是长方体,长、宽约2.4米,高约15米,它的体积大约是多少?
V=a b h
=2.4×2.4×15
=86.4(立方米)
答:它的体积是86.4立方米。
3、一堆砖摆成长方体形状,长4米,宽20分米,高23分米,如果每立方米有500块砖,这堆砖共有多少块?
答:这堆砖共有9200块。
20分米=2米
23分米=2.3米
4×2×2.3=18.4(m )
18.4×500=9200(块)
4、学校运来7.6平方米的沙子,铺在一个长5米、宽38分米的沙坑里,可以铺多厚?
38分米=3.8米
S=5×3.8=19(平方米)
h=V÷S=7.6÷19=0.4(米)
答:可以铺0.4米厚。
5、一个游泳池长50米,宽21米,深2.5米。如果给游泳池注入2米深的水,每小时注入150立方米,几小时能注入完?
V=a b h
=50×21×2
=2100(立方米)
2100÷150=14(小时)
答:14小时能注入完。
6、把一个棱长8厘米的正方体钢块,锻造成长16厘米,宽5厘米的长方体钢板,这钢板厚多少厘米?
V=a
=8×8×8=512(立方厘米)
S=16×5=80(平方厘米)
答:这钢板厚6.4厘米。
h=V÷S=512÷80=6.4(厘米)
7、一段长为20分米的长方体木料,将它截成5段后,表面积增加40平方分米。这根木料原来的体积是多少?
(5-1)×2=8(个)
40÷8=5(平方分米)
答:这根木料原来的体积是100立方分米。
V=S h=5×20=100(立方分米)
8、一个长方体,如果长增加2cm,则体积增加40cm ;如果宽增加3cm,则体积增加90cm ;如果高增加4cm,则体积增加96cm 。求原长方体的表面积。
40÷2=20(cm )
90÷3=30(cm )
96÷4=24(cm )
(20+30+24)×2=148(cm )
答:原长方体的表面积为148平方厘米。
9、—个长方体木块,从下部和上部分别截去高为3cm和2cm的长方体后,便成为一个正方体,其表面积减少了120cm 。原来长方体的体积是多少立方厘米
120÷4÷(2+3)=6(cm)
6×6×(6+3+2)=396(cm )
答:原长方体的体积是396立方厘米。
感
谢
聆
听
