5.2 运动的合成与分解 同步练习题(word版含答案)
文档属性
| 名称 | 5.2 运动的合成与分解 同步练习题(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 408.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-23 05:44:55 | ||
图片预览




文档简介
5.2 运动的合成与分解
一、单选题
1.如图,长为L的轻直棒一端可绕固定轴O在竖直面内转动,另一端固定一质量为m的小球,小球搁在光滑水平升降台上,升降平台一速度v匀速上升。下列说法正确的是( )
A.小球做匀速圆周运动 B.棒的角速度逐渐增大
C.当棒与竖直方向的夹角为时,小球的速度为
D.当棒与竖直方向的夹角为时,棒的角速度为
2.在光滑水平面内有一个直角坐标系,某一物体在该平面内分别沿轴方向的位移—时间图像和沿轴方向的速度—时间图像分别如甲、乙图所示。对于物体在0~4s内的运动情况,下列说法中正确的是( )
A.时刻,物体的加速度大小为 B.0~4s内,物体做匀变速曲线运动
C.时,物体的初速度大小为3m/s D.0~4s内,物体的位移大小为4m
3.关于曲线运动的描述,下列说法正确的是( )
A.曲线运动一定是变速运动
B.物体在恒力作用下,不可能做曲线运动
C.物体在变力作用下一定做曲线运动
D.两个变速运动的合运动必为曲线运动
4.如图所示,船头始终保持与河岸成θ角渡河,已知船在静水中的速度为v,水速平行于河岸,大小为u,河宽为d,则( )
A.船渡河的时间为
B.船可能在图中A点处到达对岸
C.船一定在图中A点下游某位置到达对岸
D.若水流的速度u增大,则船渡河的时间也将增加
5.小船在静水中的速度为3 m/s,它在一条流速为4 m/s,河宽为150 m的河流中渡河,则( )
A.小船不可能垂直河岸到达河对岸
B.小船渡河的时间可能为40s
C.小船渡河的时间至少为30s
D.小船若在50s内渡河,到达河对岸时被冲下150m远
6.两端封闭的玻璃管中注满清水,迅速将管转至图示竖直位置,管内一个红蜡块立即以的速度匀速上浮,此时使玻璃管沿x轴正方向移动,当玻璃管沿x轴( )
A.匀速运动时,红蜡块的轨迹是一条曲线
B.以速度匀速运动时,红蜡块的速度大小是7cm/s
C.以速度匀速运动,2s内红蜡块的位移大小是10cm
D.由静止开始做的匀加速运动时,红蜡块的轨迹是一条直线
二、多选题
7.如图所示,当放在墙角的均匀直杆端在竖直墙上,端放在水平地面,当滑到图示位置时(已知),端速度为,下列说法正确的有( )
A.端和端垂直杆方向的速度分量大小一定相等
B.端和端沿杆方向的速度分量大小一定相等
C.端速度大小为
D.端速度大小为
8.一只小船在静水中的速度大小为8m/s,在流速为4m/s的河中航行时,船的实际航行速度大小可能是( )
A.1m/s B.5m/s C.8m/s D.14m/s
9.质量为m的物体P置于倾角为θ1的固定光滑斜面上,轻细绳跨过光滑轻质定滑轮分别连接着P与小车,P与滑轮间的细绳平行于斜面,小车以速率v水平向右做匀速直线运动。当小车与滑轮间的细绳和水平方向成夹角θ2时,下列判断正确的是( )
A.P的速率为vcosθ2
B.P的速率为
C.物体P也沿斜面做匀速运动
D.物体P沿斜面做加速运动
10.关于运动的合成与分解,下列说法正确的是( )
A.合运动的位移是分运动位移的矢量和
B.合运动的速度一定会比其中任何一个分速度大
C.合运动的时间与分运动的时间相等
D.若合运动是曲线运动,则分运动中至少有一个是曲线运动
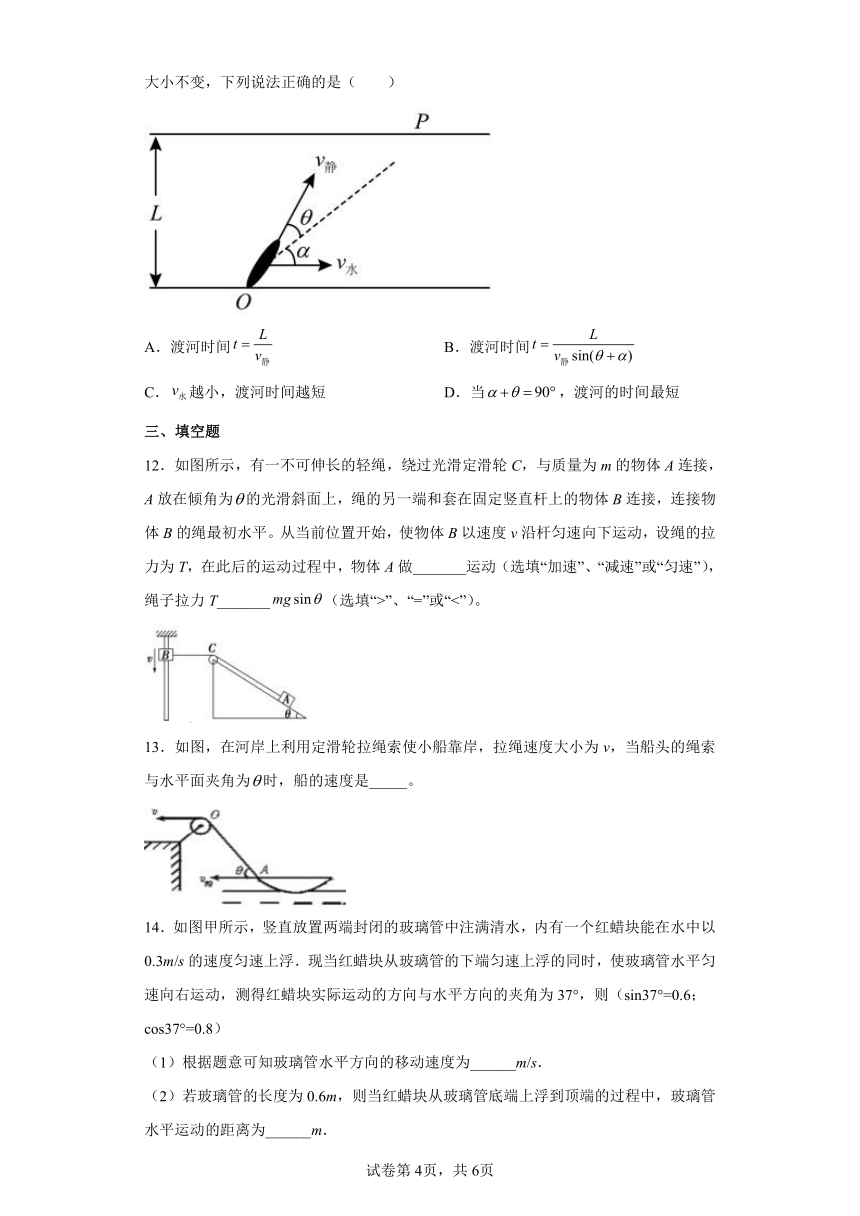
11.如图所示,小船从河岸的O点沿虚线运动轨迹,匀速运动到河对岸的P点,河水的流速、船在静水中的速度与虚线的夹角分别为,,河宽为L,且、的大小不变,下列说法正确的是( )
A.渡河时间 B.渡河时间
C.越小,渡河时间越短 D.当,渡河的时间最短
三、填空题
12.如图所示,有一不可伸长的轻绳,绕过光滑定滑轮C,与质量为m的物体A连接,A放在倾角为的光滑斜面上,绳的另一端和套在固定竖直杆上的物体B连接,连接物体B的绳最初水平。从当前位置开始,使物体B以速度v沿杆匀速向下运动,设绳的拉力为T,在此后的运动过程中,物体A做_______运动(选填“加速”、“减速”或“匀速”),绳子拉力T_______(选填“>”、“=”或“<”)。
13.如图,在河岸上利用定滑轮拉绳索使小船靠岸,拉绳速度大小为v,当船头的绳索与水平面夹角为时,船的速度是_____。
14.如图甲所示,竖直放置两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以0.3m/s的速度匀速上浮.现当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动的方向与水平方向的夹角为37°,则(sin37°=0.6;cos37°=0.8)
(1)根据题意可知玻璃管水平方向的移动速度为______m/s.
(2)若玻璃管的长度为0.6m,则当红蜡块从玻璃管底端上浮到顶端的过程中,玻璃管水平运动的距离为______m.
(3)如图乙所示,若红蜡块从A点匀速上浮的同时,使玻璃管水平向右作匀加速直线运动,则红蜡块实际运动的轨迹是图中的______
A.直线P B.曲线Q C.曲线R D.无法确定.
15.如图,一块木块用细线悬挂于O点,现用一钉子贴着细线的左侧,沿与水平方向成30°角的斜面向右以速度υ匀速移动,移动中始终保持悬线竖直,到图中虚线位置时,木块速度的大小为________,与水平方向夹角为________。
四、解答题
16.在工厂车间里传送工件时常会用到改变方向的传送装置,如图所示,生产车间有两个相互垂直且等高的水平传送带甲和乙,甲匀速运行的速度为,工件离开甲前与甲的速度相同,并平稳地传到乙上,工件与甲和乙之间的动摩擦因数均为,乙的宽度足够大,工件不会从右侧滑出,重力加速度为。
(1)某工件从甲传送带距甲、乙传送带的分界线处轻放,问经过多长时间该工件可以到达乙传送带?
(2)若乙的速度也为,且乙的长度足够,求工件在乙传送带上的痕迹长度?工件在乙传送带上运动(对地)速度的最小值为多少?
17.如图所示,光滑水平面内有一直角坐标系xOy,O为坐标系的原点。有一质量m=1kg的可视为质点的物体静止于原点O,现对其施加一沿x轴正方向的力F1,经过t1=4s后物体到达坐标为(8m,0)的位置。第4 s末撤去F1,改为施加沿y轴正方向的力F2=2N。求∶
(1)F1的大小;
(2)第6s末物体的速度大小和速度与x轴正方向的夹角的正切值。
18.小船摆渡曾是人们过河的主要方式。设河的宽度为d,河水匀速流动,流速为,小船在静水中的运动速度为,且>。
(1)要使小船渡河的时间最短,小船应如何渡河?最短时间是多少?到达对岸时小船的航程是多少?
(2)要使小船渡河的航程最短,小船应如何渡河?渡河所用的时间是多少?最短的航程是多少?
试卷第1页,共3页
试卷第6页,共6页
参考答案:
1.C
【解析】
【详解】
棒与平台接触点的实际运动即合运动方向是垂直于棒指向左上,如图所示
合速度
沿竖直方向上的速度分量v满足
所以
升降平台向上匀速运动,v恒定,夹角增大,角速度减小,小球不是做匀速圆周运动,故ABD错误,C正确。
故选C。
2.B
【解析】
【详解】
由图可知,物体在轴方向做匀速直线运动,速度为1m/s,在轴方向做初速度为3m/s的匀减速直线运动,由图无法求出加速度
C.时,物体的初速度大小为
故C错误;
A.无法根据图乙求出加速度大小,故A错误;
B.0~4s内,物体的加速度沿y轴方向,初速度的方向和加速度方向不在同一条直线,所以物体做匀变速曲线运动,故B正确;
D.0~4s内,物体在轴方向方向的位移为4m,轴方向的位移无法求出,所以无法求出物体位移的大小,故D错误。
故选B。
3.A
【解析】
【详解】
A.曲线运动的速度方向一直在变,所以一定是变速运动,故A正确;
B.物体在恒力作用下也可能做曲线运动,只要力的方向始终不和速度方向共线即可,故B错误;
C.当变力始终与物体速度共线时,物体在该力作用下将做变加速直线运动,故C错误;
D. 若两个变速直线运动的合力与速度在一条直线上,则合运动为匀变速直线运动,故D错误。
故选A。
4.C
【解析】
【详解】
A.船在渡河时,由于水流有速度,则船不沿船头方向运动,把船的速度分解到沿着河岸和垂直河岸方向,垂直河岸方向的速度
则渡河时间
故A错误;
BC.由图可知,根据矢量求合法则,船的合速度方向,也就是船行驶的方向,一定在船速度方向和水流速度方向夹角范围内,则一定不指向A,指向A下游的某一位置,故B错误C正确;
D.水流的速度u增大,不影响垂直河岸方向的速度,则渡河时间不变,故D错误。
故选C。
5.A
【解析】
【详解】
A.由于船的速度小于水流的速度,因此小船不可能垂直河岸到达河对岸,A 正确;
BC.当船头指向正对岸时,过河的时间最短,且最短时间为
BC错误;
D.小船若在50s内渡河,船头指向正对岸,到达河对岸时,被冲到下游距离
D错误。
故选A。
6.C
【解析】
【详解】
A.当玻璃管沿x轴匀速运动时,红蜡块的合运动为匀速直线运动,其轨迹是一条直线,故A错误;
BC.当玻璃管沿x轴以速度匀速运动时,红蜡块的速度大小是
2s内红蜡块的位移大小是
故B错误,C正确;
D.当玻璃管沿x轴由静止开始做的匀加速运动时,红蜡块的合运动为曲线运动,其轨迹是一条曲线,故D错误。
故选C。
7.BD
【解析】
【详解】
AB.将物体A端和B端的运动分解到沿杆和垂直于杆的方向如图所示
A端和B端沿杆方向的速度分量大小一定相等,垂直于杆的速度分量大小不一定相等,故A错误,B正确;
CD.设沿杆速度为,根据速度的合成与分解,将两个端点的速度分解,如图所示
则有
而
则两个端点实际速度之比
则A点速度是
故C错误,D正确。
故选BD。
8.BC
【解析】
【详解】
由平行四边形定则可得出小船合速度的范围是大于或等于4m/s,小于或等于12m/s,其间的任一速度值都有可能,故选BC。
9.AD
【解析】
【详解】
AB.将小车的速度进行分解,如图
故A正确;B错误;
CD.根据上式分析,可知小车匀速向右匀速运动,减小,增大,所以物体P沿斜面做加速运动。故C错误;D正确。
故选AD。
10.AC
【解析】
【分析】
【详解】
A.位移是矢量,合位移是分位移的矢量和,选项A正确;
B.速度也是矢量,满足平行四边形定则,根据平行四边形的特点,合速度可能比分速度小,选项B错误;
C.根据合运动与分运动的等时性,选项C正确;
D.两个直线运动的合运动也可以是曲线运动,例如,互成夹角的匀速直线运动与匀加速直线运动合成时,合运动是曲线运动,选项D错误。
故选AC。
11.BD
【解析】
【详解】
ABC.渡河的时间
与无关,选项AC错误,B正确;
D.当,渡河时间最短
D正确。
故选BD。
12. 加速 >
【解析】
【详解】
由图可知绳端的速度为
与B的位置有关,因为B为匀速运动,B下降过程中α变大,因此物体A做加速运动;
物体A做加速运动,所以绳子拉力
T>
13.
【解析】
【详解】
船的速度等于沿绳子方向和垂直于绳子方向速度的合速度,根据平行四边形定则,有
则
14. 0.4 0.8 B
【解析】
【详解】
解:(1)根据平行四边形定则,有:
则有:
(2)在竖直方向上运动的时间为:
则玻璃管在水平方向上运动的距离为:
(3)根据运动的合成与分解,运动的轨迹偏向合外力的方向,则有Q,故选项B正确,A、C、D错误.
15. v 60°
【解析】
【详解】
橡皮沿与水平方向成30°的斜面向右以速度v匀速运动,由于橡皮沿与水平方向成30°的斜面向右以速度v匀速运动的位移一定等于橡皮向上的位移,故在竖直方向以相等的速度匀速运动,根据平行四边形定则,可知合速度也是一定的,故合运动是匀速运动;
根据平行四边形定则求得合速度大小
v合=2vcos30°=v
方向不变和水平方向成60°。
16.(1)2.75s;(2)4.5m;m/s
【解析】
【详解】
(1)工件在甲先匀加速运动,加速度大小
=2m/s2
t1==1.5s
x1=2.25m
后匀速,用时为
t2==1.25s
总用时
t=t1+t2=2.75s
(2)方法一:在传送带乙上,工件与传送带相对运动时,所受摩擦力的大小和方向不变,其大小
f=μmg
工件的加速度大小
=μg
方向与侧向的夹角为α=45°;
小工件沿x方向做匀减速直线运动,加速度大小
x=cos45°=m/s2
=0-
解得
x=m
匀减速至零用时
==s
沿y方向做匀加速
y=sin=m/s2
位移
y==m
相对乙的y方向位移
y=v0-y=m
工件相对乙的位移(痕迹的长度)
==4.5m
方法二:以传送带乙为参考系,工件做初速度
v=3m/s
加速度==2m/s2的匀减速直线运动,直至相对静止;
则痕迹的长度
s==4.5m
以地为参考系,工件在乙传送带上相对滑动时可视为做类斜抛运动,其偏转角90°,根据对称性,可得工件初速沿垂直摩擦力方向的分速度大小就是最小速度,等效为斜抛运动达最高点
v1=v0cos45°=m/s
17.(1)1N;(2),1
【解析】
【详解】
(1)经过t1=4s后物体的位移为x1=8m,由运动学公式可得
解得a1=1m/s2,由牛顿第二定律可得
此时沿x轴的速度大小为
(2)4s后沿y轴的加速度大小为
第6s末沿y轴的分速度为
合速度大小为
x轴正方向的夹角的正切值为
18.(1)船头的方向应垂直于对岸;;;(2)合速度方向应垂直于对岸;;d
【解析】
【详解】
(1)要使小船渡河的时间最短,小船在静水中的速度应全部用于过河,因此船头的方向应垂直于对岸,小船速度的合成如图所示,则最短渡河时间
小船的速度
故到达对岸时小船的航程
(2)要使小船渡河的航程最短,小船的合速度方向应垂直于对岸,即船头需向上游转过一定的角度。因为>,小船速度的合成如图所示,则小船的速度
最短的航程即为河的宽度d,故渡河所用的时间
船头方向与对岸的夹角可通过
求得
答案第1页,共2页
答案第12页,共1页
一、单选题
1.如图,长为L的轻直棒一端可绕固定轴O在竖直面内转动,另一端固定一质量为m的小球,小球搁在光滑水平升降台上,升降平台一速度v匀速上升。下列说法正确的是( )
A.小球做匀速圆周运动 B.棒的角速度逐渐增大
C.当棒与竖直方向的夹角为时,小球的速度为
D.当棒与竖直方向的夹角为时,棒的角速度为
2.在光滑水平面内有一个直角坐标系,某一物体在该平面内分别沿轴方向的位移—时间图像和沿轴方向的速度—时间图像分别如甲、乙图所示。对于物体在0~4s内的运动情况,下列说法中正确的是( )
A.时刻,物体的加速度大小为 B.0~4s内,物体做匀变速曲线运动
C.时,物体的初速度大小为3m/s D.0~4s内,物体的位移大小为4m
3.关于曲线运动的描述,下列说法正确的是( )
A.曲线运动一定是变速运动
B.物体在恒力作用下,不可能做曲线运动
C.物体在变力作用下一定做曲线运动
D.两个变速运动的合运动必为曲线运动
4.如图所示,船头始终保持与河岸成θ角渡河,已知船在静水中的速度为v,水速平行于河岸,大小为u,河宽为d,则( )
A.船渡河的时间为
B.船可能在图中A点处到达对岸
C.船一定在图中A点下游某位置到达对岸
D.若水流的速度u增大,则船渡河的时间也将增加
5.小船在静水中的速度为3 m/s,它在一条流速为4 m/s,河宽为150 m的河流中渡河,则( )
A.小船不可能垂直河岸到达河对岸
B.小船渡河的时间可能为40s
C.小船渡河的时间至少为30s
D.小船若在50s内渡河,到达河对岸时被冲下150m远
6.两端封闭的玻璃管中注满清水,迅速将管转至图示竖直位置,管内一个红蜡块立即以的速度匀速上浮,此时使玻璃管沿x轴正方向移动,当玻璃管沿x轴( )
A.匀速运动时,红蜡块的轨迹是一条曲线
B.以速度匀速运动时,红蜡块的速度大小是7cm/s
C.以速度匀速运动,2s内红蜡块的位移大小是10cm
D.由静止开始做的匀加速运动时,红蜡块的轨迹是一条直线
二、多选题
7.如图所示,当放在墙角的均匀直杆端在竖直墙上,端放在水平地面,当滑到图示位置时(已知),端速度为,下列说法正确的有( )
A.端和端垂直杆方向的速度分量大小一定相等
B.端和端沿杆方向的速度分量大小一定相等
C.端速度大小为
D.端速度大小为
8.一只小船在静水中的速度大小为8m/s,在流速为4m/s的河中航行时,船的实际航行速度大小可能是( )
A.1m/s B.5m/s C.8m/s D.14m/s
9.质量为m的物体P置于倾角为θ1的固定光滑斜面上,轻细绳跨过光滑轻质定滑轮分别连接着P与小车,P与滑轮间的细绳平行于斜面,小车以速率v水平向右做匀速直线运动。当小车与滑轮间的细绳和水平方向成夹角θ2时,下列判断正确的是( )
A.P的速率为vcosθ2
B.P的速率为
C.物体P也沿斜面做匀速运动
D.物体P沿斜面做加速运动
10.关于运动的合成与分解,下列说法正确的是( )
A.合运动的位移是分运动位移的矢量和
B.合运动的速度一定会比其中任何一个分速度大
C.合运动的时间与分运动的时间相等
D.若合运动是曲线运动,则分运动中至少有一个是曲线运动
11.如图所示,小船从河岸的O点沿虚线运动轨迹,匀速运动到河对岸的P点,河水的流速、船在静水中的速度与虚线的夹角分别为,,河宽为L,且、的大小不变,下列说法正确的是( )
A.渡河时间 B.渡河时间
C.越小,渡河时间越短 D.当,渡河的时间最短
三、填空题
12.如图所示,有一不可伸长的轻绳,绕过光滑定滑轮C,与质量为m的物体A连接,A放在倾角为的光滑斜面上,绳的另一端和套在固定竖直杆上的物体B连接,连接物体B的绳最初水平。从当前位置开始,使物体B以速度v沿杆匀速向下运动,设绳的拉力为T,在此后的运动过程中,物体A做_______运动(选填“加速”、“减速”或“匀速”),绳子拉力T_______(选填“>”、“=”或“<”)。
13.如图,在河岸上利用定滑轮拉绳索使小船靠岸,拉绳速度大小为v,当船头的绳索与水平面夹角为时,船的速度是_____。
14.如图甲所示,竖直放置两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中以0.3m/s的速度匀速上浮.现当红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动的方向与水平方向的夹角为37°,则(sin37°=0.6;cos37°=0.8)
(1)根据题意可知玻璃管水平方向的移动速度为______m/s.
(2)若玻璃管的长度为0.6m,则当红蜡块从玻璃管底端上浮到顶端的过程中,玻璃管水平运动的距离为______m.
(3)如图乙所示,若红蜡块从A点匀速上浮的同时,使玻璃管水平向右作匀加速直线运动,则红蜡块实际运动的轨迹是图中的______
A.直线P B.曲线Q C.曲线R D.无法确定.
15.如图,一块木块用细线悬挂于O点,现用一钉子贴着细线的左侧,沿与水平方向成30°角的斜面向右以速度υ匀速移动,移动中始终保持悬线竖直,到图中虚线位置时,木块速度的大小为________,与水平方向夹角为________。
四、解答题
16.在工厂车间里传送工件时常会用到改变方向的传送装置,如图所示,生产车间有两个相互垂直且等高的水平传送带甲和乙,甲匀速运行的速度为,工件离开甲前与甲的速度相同,并平稳地传到乙上,工件与甲和乙之间的动摩擦因数均为,乙的宽度足够大,工件不会从右侧滑出,重力加速度为。
(1)某工件从甲传送带距甲、乙传送带的分界线处轻放,问经过多长时间该工件可以到达乙传送带?
(2)若乙的速度也为,且乙的长度足够,求工件在乙传送带上的痕迹长度?工件在乙传送带上运动(对地)速度的最小值为多少?
17.如图所示,光滑水平面内有一直角坐标系xOy,O为坐标系的原点。有一质量m=1kg的可视为质点的物体静止于原点O,现对其施加一沿x轴正方向的力F1,经过t1=4s后物体到达坐标为(8m,0)的位置。第4 s末撤去F1,改为施加沿y轴正方向的力F2=2N。求∶
(1)F1的大小;
(2)第6s末物体的速度大小和速度与x轴正方向的夹角的正切值。
18.小船摆渡曾是人们过河的主要方式。设河的宽度为d,河水匀速流动,流速为,小船在静水中的运动速度为,且>。
(1)要使小船渡河的时间最短,小船应如何渡河?最短时间是多少?到达对岸时小船的航程是多少?
(2)要使小船渡河的航程最短,小船应如何渡河?渡河所用的时间是多少?最短的航程是多少?
试卷第1页,共3页
试卷第6页,共6页
参考答案:
1.C
【解析】
【详解】
棒与平台接触点的实际运动即合运动方向是垂直于棒指向左上,如图所示
合速度
沿竖直方向上的速度分量v满足
所以
升降平台向上匀速运动,v恒定,夹角增大,角速度减小,小球不是做匀速圆周运动,故ABD错误,C正确。
故选C。
2.B
【解析】
【详解】
由图可知,物体在轴方向做匀速直线运动,速度为1m/s,在轴方向做初速度为3m/s的匀减速直线运动,由图无法求出加速度
C.时,物体的初速度大小为
故C错误;
A.无法根据图乙求出加速度大小,故A错误;
B.0~4s内,物体的加速度沿y轴方向,初速度的方向和加速度方向不在同一条直线,所以物体做匀变速曲线运动,故B正确;
D.0~4s内,物体在轴方向方向的位移为4m,轴方向的位移无法求出,所以无法求出物体位移的大小,故D错误。
故选B。
3.A
【解析】
【详解】
A.曲线运动的速度方向一直在变,所以一定是变速运动,故A正确;
B.物体在恒力作用下也可能做曲线运动,只要力的方向始终不和速度方向共线即可,故B错误;
C.当变力始终与物体速度共线时,物体在该力作用下将做变加速直线运动,故C错误;
D. 若两个变速直线运动的合力与速度在一条直线上,则合运动为匀变速直线运动,故D错误。
故选A。
4.C
【解析】
【详解】
A.船在渡河时,由于水流有速度,则船不沿船头方向运动,把船的速度分解到沿着河岸和垂直河岸方向,垂直河岸方向的速度
则渡河时间
故A错误;
BC.由图可知,根据矢量求合法则,船的合速度方向,也就是船行驶的方向,一定在船速度方向和水流速度方向夹角范围内,则一定不指向A,指向A下游的某一位置,故B错误C正确;
D.水流的速度u增大,不影响垂直河岸方向的速度,则渡河时间不变,故D错误。
故选C。
5.A
【解析】
【详解】
A.由于船的速度小于水流的速度,因此小船不可能垂直河岸到达河对岸,A 正确;
BC.当船头指向正对岸时,过河的时间最短,且最短时间为
BC错误;
D.小船若在50s内渡河,船头指向正对岸,到达河对岸时,被冲到下游距离
D错误。
故选A。
6.C
【解析】
【详解】
A.当玻璃管沿x轴匀速运动时,红蜡块的合运动为匀速直线运动,其轨迹是一条直线,故A错误;
BC.当玻璃管沿x轴以速度匀速运动时,红蜡块的速度大小是
2s内红蜡块的位移大小是
故B错误,C正确;
D.当玻璃管沿x轴由静止开始做的匀加速运动时,红蜡块的合运动为曲线运动,其轨迹是一条曲线,故D错误。
故选C。
7.BD
【解析】
【详解】
AB.将物体A端和B端的运动分解到沿杆和垂直于杆的方向如图所示
A端和B端沿杆方向的速度分量大小一定相等,垂直于杆的速度分量大小不一定相等,故A错误,B正确;
CD.设沿杆速度为,根据速度的合成与分解,将两个端点的速度分解,如图所示
则有
而
则两个端点实际速度之比
则A点速度是
故C错误,D正确。
故选BD。
8.BC
【解析】
【详解】
由平行四边形定则可得出小船合速度的范围是大于或等于4m/s,小于或等于12m/s,其间的任一速度值都有可能,故选BC。
9.AD
【解析】
【详解】
AB.将小车的速度进行分解,如图
故A正确;B错误;
CD.根据上式分析,可知小车匀速向右匀速运动,减小,增大,所以物体P沿斜面做加速运动。故C错误;D正确。
故选AD。
10.AC
【解析】
【分析】
【详解】
A.位移是矢量,合位移是分位移的矢量和,选项A正确;
B.速度也是矢量,满足平行四边形定则,根据平行四边形的特点,合速度可能比分速度小,选项B错误;
C.根据合运动与分运动的等时性,选项C正确;
D.两个直线运动的合运动也可以是曲线运动,例如,互成夹角的匀速直线运动与匀加速直线运动合成时,合运动是曲线运动,选项D错误。
故选AC。
11.BD
【解析】
【详解】
ABC.渡河的时间
与无关,选项AC错误,B正确;
D.当,渡河时间最短
D正确。
故选BD。
12. 加速 >
【解析】
【详解】
由图可知绳端的速度为
与B的位置有关,因为B为匀速运动,B下降过程中α变大,因此物体A做加速运动;
物体A做加速运动,所以绳子拉力
T>
13.
【解析】
【详解】
船的速度等于沿绳子方向和垂直于绳子方向速度的合速度,根据平行四边形定则,有
则
14. 0.4 0.8 B
【解析】
【详解】
解:(1)根据平行四边形定则,有:
则有:
(2)在竖直方向上运动的时间为:
则玻璃管在水平方向上运动的距离为:
(3)根据运动的合成与分解,运动的轨迹偏向合外力的方向,则有Q,故选项B正确,A、C、D错误.
15. v 60°
【解析】
【详解】
橡皮沿与水平方向成30°的斜面向右以速度v匀速运动,由于橡皮沿与水平方向成30°的斜面向右以速度v匀速运动的位移一定等于橡皮向上的位移,故在竖直方向以相等的速度匀速运动,根据平行四边形定则,可知合速度也是一定的,故合运动是匀速运动;
根据平行四边形定则求得合速度大小
v合=2vcos30°=v
方向不变和水平方向成60°。
16.(1)2.75s;(2)4.5m;m/s
【解析】
【详解】
(1)工件在甲先匀加速运动,加速度大小
=2m/s2
t1==1.5s
x1=2.25m
后匀速,用时为
t2==1.25s
总用时
t=t1+t2=2.75s
(2)方法一:在传送带乙上,工件与传送带相对运动时,所受摩擦力的大小和方向不变,其大小
f=μmg
工件的加速度大小
=μg
方向与侧向的夹角为α=45°;
小工件沿x方向做匀减速直线运动,加速度大小
x=cos45°=m/s2
=0-
解得
x=m
匀减速至零用时
==s
沿y方向做匀加速
y=sin=m/s2
位移
y==m
相对乙的y方向位移
y=v0-y=m
工件相对乙的位移(痕迹的长度)
==4.5m
方法二:以传送带乙为参考系,工件做初速度
v=3m/s
加速度==2m/s2的匀减速直线运动,直至相对静止;
则痕迹的长度
s==4.5m
以地为参考系,工件在乙传送带上相对滑动时可视为做类斜抛运动,其偏转角90°,根据对称性,可得工件初速沿垂直摩擦力方向的分速度大小就是最小速度,等效为斜抛运动达最高点
v1=v0cos45°=m/s
17.(1)1N;(2),1
【解析】
【详解】
(1)经过t1=4s后物体的位移为x1=8m,由运动学公式可得
解得a1=1m/s2,由牛顿第二定律可得
此时沿x轴的速度大小为
(2)4s后沿y轴的加速度大小为
第6s末沿y轴的分速度为
合速度大小为
x轴正方向的夹角的正切值为
18.(1)船头的方向应垂直于对岸;;;(2)合速度方向应垂直于对岸;;d
【解析】
【详解】
(1)要使小船渡河的时间最短,小船在静水中的速度应全部用于过河,因此船头的方向应垂直于对岸,小船速度的合成如图所示,则最短渡河时间
小船的速度
故到达对岸时小船的航程
(2)要使小船渡河的航程最短,小船的合速度方向应垂直于对岸,即船头需向上游转过一定的角度。因为>,小船速度的合成如图所示,则小船的速度
最短的航程即为河的宽度d,故渡河所用的时间
船头方向与对岸的夹角可通过
求得
答案第1页,共2页
答案第12页,共1页
