5.4 平移(基础讲解)(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
5.4 平移
【学习目标】
了解图形的平移变换,知道一个图形进行平移后所得的图形与原图形之间所具有的联系和性质,能用平移变换有关知识说明一些简单问题及进行图形设计.21世纪教育网版权所有
【知识总结】
一、平移
1. 定义:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种移动叫做平移.
【注】
(1)图形的平移的两要素:平移的方向与平移的距离.
(2)图形的平移不改变图形的形状与大小,只改变图形的位置.
2. 性质:
图形的平移实质上是将图形上所有点沿同一方向移动相同的距离,平移不改变线段、角的大小,具体来说:
(1)平移后,对应线段平行且相等;
(2)平移后,对应角相等;
(3)平移后,对应点所连线段平行且相等;
(4)平移后,新图形与原图形是一对全等图形.
【注】
(1)“连接各组对应点的线段”的线段的长度实际上就是平移的距离.
(2)要注意“连接各组对应点的线段”与“对应 ( http: / / www.21cnjy.com )线段”的区别,前者是通过连接平移前后的对应点得到的,而后者是原来的图形与平移后的图形上本身存在的.21教育网
3. 作图:
平移作图是平移基本性质的应用,在具体作图时,应抓住作图的“四步曲”——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点;
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图形顺次连接对应点.
【典型例题】
【类型】一、 平移
例1.如图所示,平移△ABC,使点A移动到点A′,画出平移后的△A′B′C′.
( http: / / www.21cnjy.com / )
【思路点拨】平移一个图形,首先要确定它 ( http: / / www.21cnjy.com )移动的方向和距离,连接AA′后这个问题便获得解决.根据平移后的图形与原来的图形的对应线段平行(或在一条直线上)且相等,容易画出所求的线段.
【答案与解析】
解:如图所示,
( http: / / www.21cnjy.com / )
(1)连接AA′,过点B作AA′的平行线,在上截取BB′=AA′,则点B′就是点B的对应点.
(2)用同样的方法做出点C的对应点C′,连接A′B′、B′C′、C′A′,
就得到平移后的三角形A′B′C′.
【点评】平移一个图形,首先要确定它移动的方向 ( http: / / www.21cnjy.com )和距离.连接AA′,这个问题就解决了,然后分别把B、C按AA′的方向平移AA′的长度,便可得到其对应点B′、C′,这就是确定了关键点平移后的位置,依次连接A′B′,B′C′,C′A′便得到平移后的三角形A′B′C′.21cnjy.com
例2. 如图所示,将△ABC沿直线AB向右平移后到达△BDE的位置,若
∠CAB=50°,∠ABC=100°,则∠CBE的度数为________.
【答案】30°
【解析】根据平移的特征可知:∠EBD=∠CAB=50°而∠ABC=100°
所以∠CBE=180°-∠EBD-∠ABC=180°-50°-100°=30°
【点评】图形在平移的过程有“一变两不 ( http: / / www.21cnjy.com )变”、“一变”是位置的变化,“两不变”是形状和大小不变.本例中由△ABC经过平移得到△BED.则有AC=BE,AB=BD,BC=DE,∠A=∠EBD,∠C=∠E,∠ABC=∠BDE.
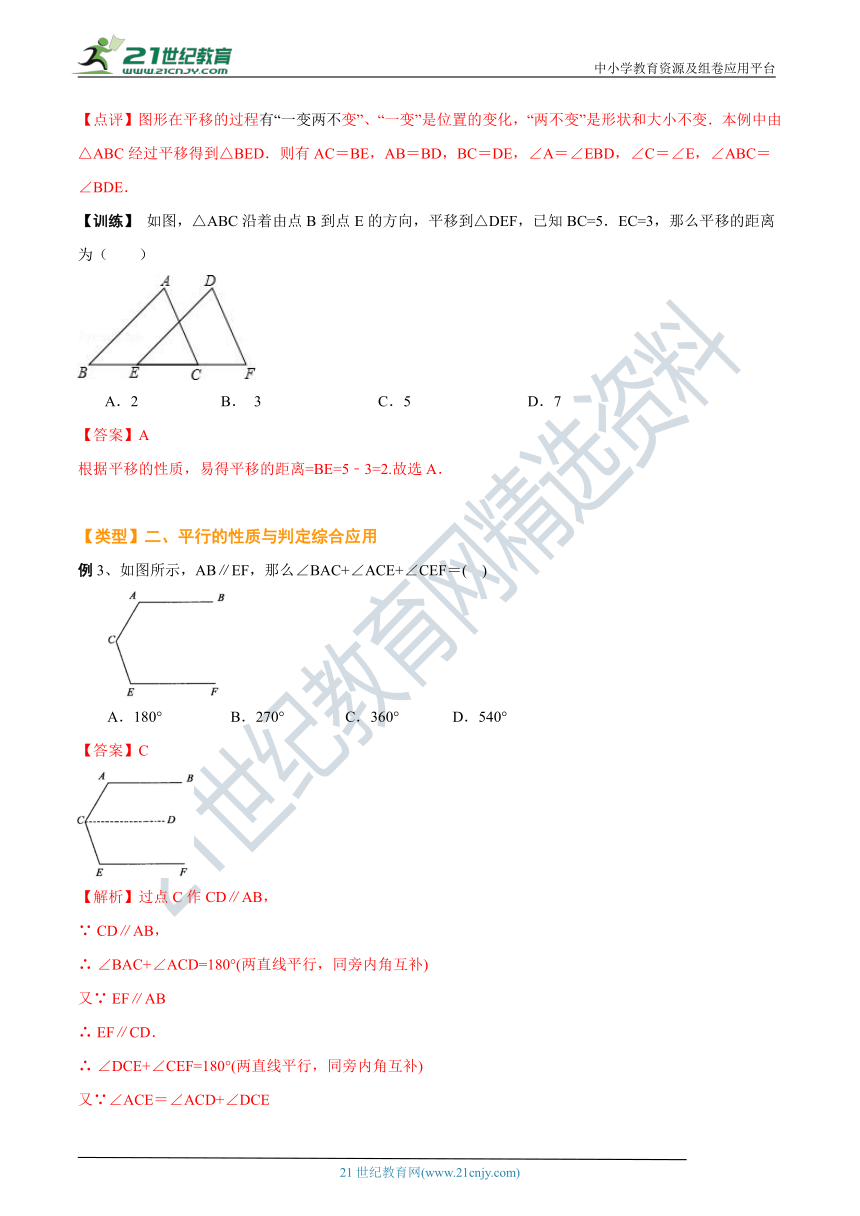
【训练】 如图,△ABC沿着由点B到点E的方向,平移到△DEF,已知BC=5.EC=3,那么平移的距离为( )21·cn·jy·com
( http: / / www.21cnjy.com / )
A.2 B. 3 C. 5 D. 7
【答案】A
根据平移的性质,易得平移的距离=BE=5﹣3=2.故选A.
【类型】二、平行的性质与判定综合应用
例3、如图所示,AB∥EF,那么∠BAC+∠ACE+∠CEF=( )
( http: / / www.21cnjy.com / )
A.180° B.270° C.360° D.540°www.21-cn-jy.com
【答案】C
( http: / / www.21cnjy.com / )
【解析】过点C作CD∥AB,
∵ CD∥AB,
∴ ∠BAC+∠ACD=180°(两直线平行,同旁内角互补)
又∵ EF∥AB
∴ EF∥CD.
∴ ∠DCE+∠CEF=180°(两直线平行,同旁内角互补)
又∵∠ACE=∠ACD+∠DCE
∴∠BAC+∠ACE+∠CEF=∠BAC+∠ACD+∠DCE+∠CEF=180°+180°=360°2·1·c·n·j·y
【点评】这是平行线性质与平行公理的综合应用,利用“两直线平行,同旁内角互补,”可以得到∠BAC +∠ACE+ ∠CEF=360°.【来源:21·世纪·教育·网】
【训练】如图所示,如果∠BAC+∠ACE+∠CEF=360°,则AB与EF的位置关系 .
【答案】平行
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
5.4 平移
【学习目标】
了解图形的平移变换,知道一个图形进行平移后所得的图形与原图形之间所具有的联系和性质,能用平移变换有关知识说明一些简单问题及进行图形设计.21世纪教育网版权所有
【知识总结】
一、平移
1. 定义:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种移动叫做平移.
【注】
(1)图形的平移的两要素:平移的方向与平移的距离.
(2)图形的平移不改变图形的形状与大小,只改变图形的位置.
2. 性质:
图形的平移实质上是将图形上所有点沿同一方向移动相同的距离,平移不改变线段、角的大小,具体来说:
(1)平移后,对应线段平行且相等;
(2)平移后,对应角相等;
(3)平移后,对应点所连线段平行且相等;
(4)平移后,新图形与原图形是一对全等图形.
【注】
(1)“连接各组对应点的线段”的线段的长度实际上就是平移的距离.
(2)要注意“连接各组对应点的线段”与“对应 ( http: / / www.21cnjy.com )线段”的区别,前者是通过连接平移前后的对应点得到的,而后者是原来的图形与平移后的图形上本身存在的.21教育网
3. 作图:
平移作图是平移基本性质的应用,在具体作图时,应抓住作图的“四步曲”——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点;
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图形顺次连接对应点.
【典型例题】
【类型】一、 平移
例1.如图所示,平移△ABC,使点A移动到点A′,画出平移后的△A′B′C′.
( http: / / www.21cnjy.com / )
【思路点拨】平移一个图形,首先要确定它 ( http: / / www.21cnjy.com )移动的方向和距离,连接AA′后这个问题便获得解决.根据平移后的图形与原来的图形的对应线段平行(或在一条直线上)且相等,容易画出所求的线段.
【答案与解析】
解:如图所示,
( http: / / www.21cnjy.com / )
(1)连接AA′,过点B作AA′的平行线,在上截取BB′=AA′,则点B′就是点B的对应点.
(2)用同样的方法做出点C的对应点C′,连接A′B′、B′C′、C′A′,
就得到平移后的三角形A′B′C′.
【点评】平移一个图形,首先要确定它移动的方向 ( http: / / www.21cnjy.com )和距离.连接AA′,这个问题就解决了,然后分别把B、C按AA′的方向平移AA′的长度,便可得到其对应点B′、C′,这就是确定了关键点平移后的位置,依次连接A′B′,B′C′,C′A′便得到平移后的三角形A′B′C′.21cnjy.com
例2. 如图所示,将△ABC沿直线AB向右平移后到达△BDE的位置,若
∠CAB=50°,∠ABC=100°,则∠CBE的度数为________.
【答案】30°
【解析】根据平移的特征可知:∠EBD=∠CAB=50°而∠ABC=100°
所以∠CBE=180°-∠EBD-∠ABC=180°-50°-100°=30°
【点评】图形在平移的过程有“一变两不 ( http: / / www.21cnjy.com )变”、“一变”是位置的变化,“两不变”是形状和大小不变.本例中由△ABC经过平移得到△BED.则有AC=BE,AB=BD,BC=DE,∠A=∠EBD,∠C=∠E,∠ABC=∠BDE.
【训练】 如图,△ABC沿着由点B到点E的方向,平移到△DEF,已知BC=5.EC=3,那么平移的距离为( )21·cn·jy·com
( http: / / www.21cnjy.com / )
A.2 B. 3 C. 5 D. 7
【答案】A
根据平移的性质,易得平移的距离=BE=5﹣3=2.故选A.
【类型】二、平行的性质与判定综合应用
例3、如图所示,AB∥EF,那么∠BAC+∠ACE+∠CEF=( )
( http: / / www.21cnjy.com / )
A.180° B.270° C.360° D.540°www.21-cn-jy.com
【答案】C
( http: / / www.21cnjy.com / )
【解析】过点C作CD∥AB,
∵ CD∥AB,
∴ ∠BAC+∠ACD=180°(两直线平行,同旁内角互补)
又∵ EF∥AB
∴ EF∥CD.
∴ ∠DCE+∠CEF=180°(两直线平行,同旁内角互补)
又∵∠ACE=∠ACD+∠DCE
∴∠BAC+∠ACE+∠CEF=∠BAC+∠ACD+∠DCE+∠CEF=180°+180°=360°2·1·c·n·j·y
【点评】这是平行线性质与平行公理的综合应用,利用“两直线平行,同旁内角互补,”可以得到∠BAC +∠ACE+ ∠CEF=360°.【来源:21·世纪·教育·网】
【训练】如图所示,如果∠BAC+∠ACE+∠CEF=360°,则AB与EF的位置关系 .
【答案】平行
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
