6.3 向心加速度 同步练习题(word版含答案)
文档属性
| 名称 | 6.3 向心加速度 同步练习题(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 464.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-23 00:00:00 | ||
图片预览


文档简介
6.3 向心加速度
一、单选题
1.图为明代出版的《天工开物》中的牛力齿轮,体现我国古代劳动人民的科学智慧。图中A、B、C为该器械的三个齿轮,牛拉动横杆带动齿轮A转动,A与B的轮齿接触良好,B与C通过横轴连接。已知三个齿轮的半径关系为RA=4RB=8RC。当牛做匀速转动时,A、B、C三个齿轮边缘的关系,下列说法正确的是( )
A.线速度之比分别为1:1:2
B.角速度之比分别为1:4:4
C.向心加速度之比4:2:1
D.周期之比1:1:2
2.大型游乐场中有一种叫“摩天轮”的娱乐设施,如图所示,坐在其中的游客随座舱的转动而做匀速圆周运动,以下说法正确的是( )
A.游客的速度不变化,加速度为零
B.游客的速度不变化,加速度也不变化
C.游客的速度要变化,加速度却不变化
D.游客的速度要变化,加速度也要变化
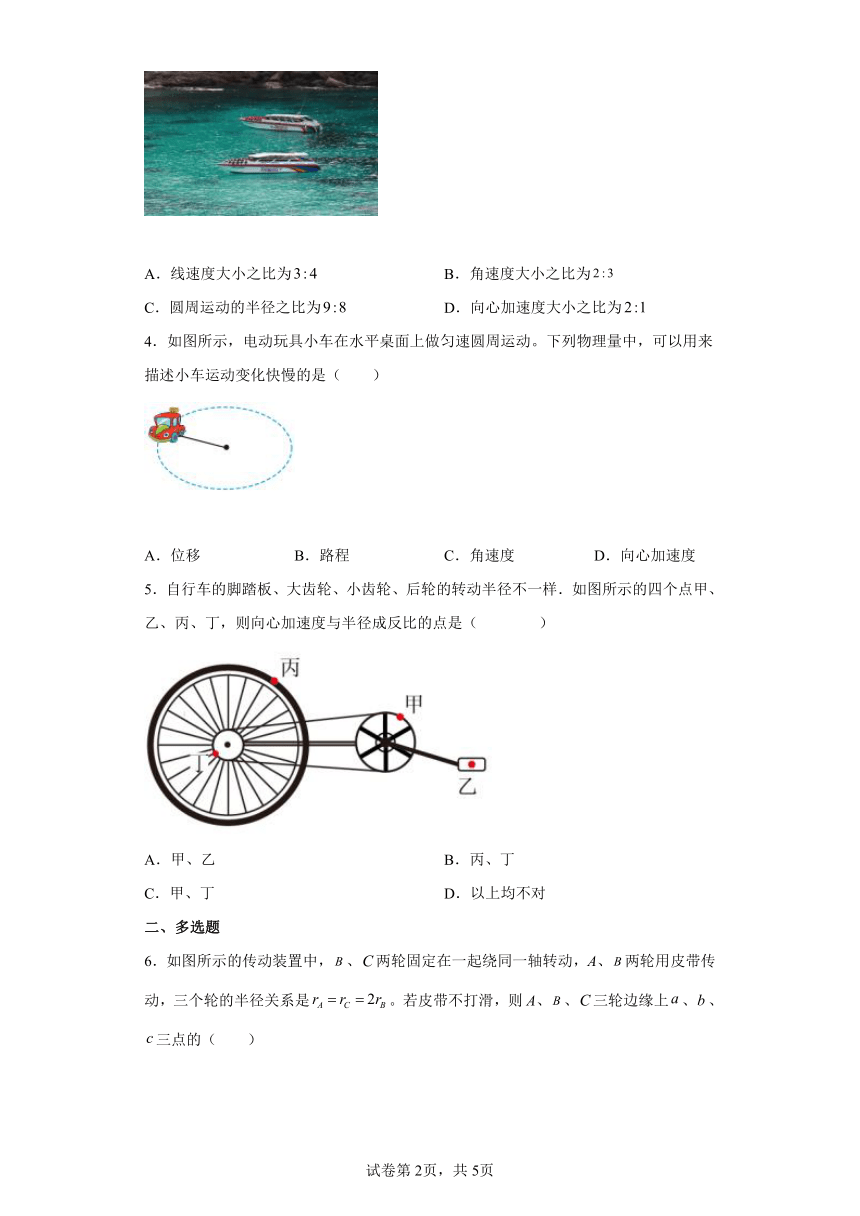
3.A、B两艘快艇在湖面上做匀速圆周运动(如图),在相同的时间内,它们通过的路程之比是,运动方向改变的角度之比是,则它们( )
A.线速度大小之比为 B.角速度大小之比为
C.圆周运动的半径之比为 D.向心加速度大小之比为
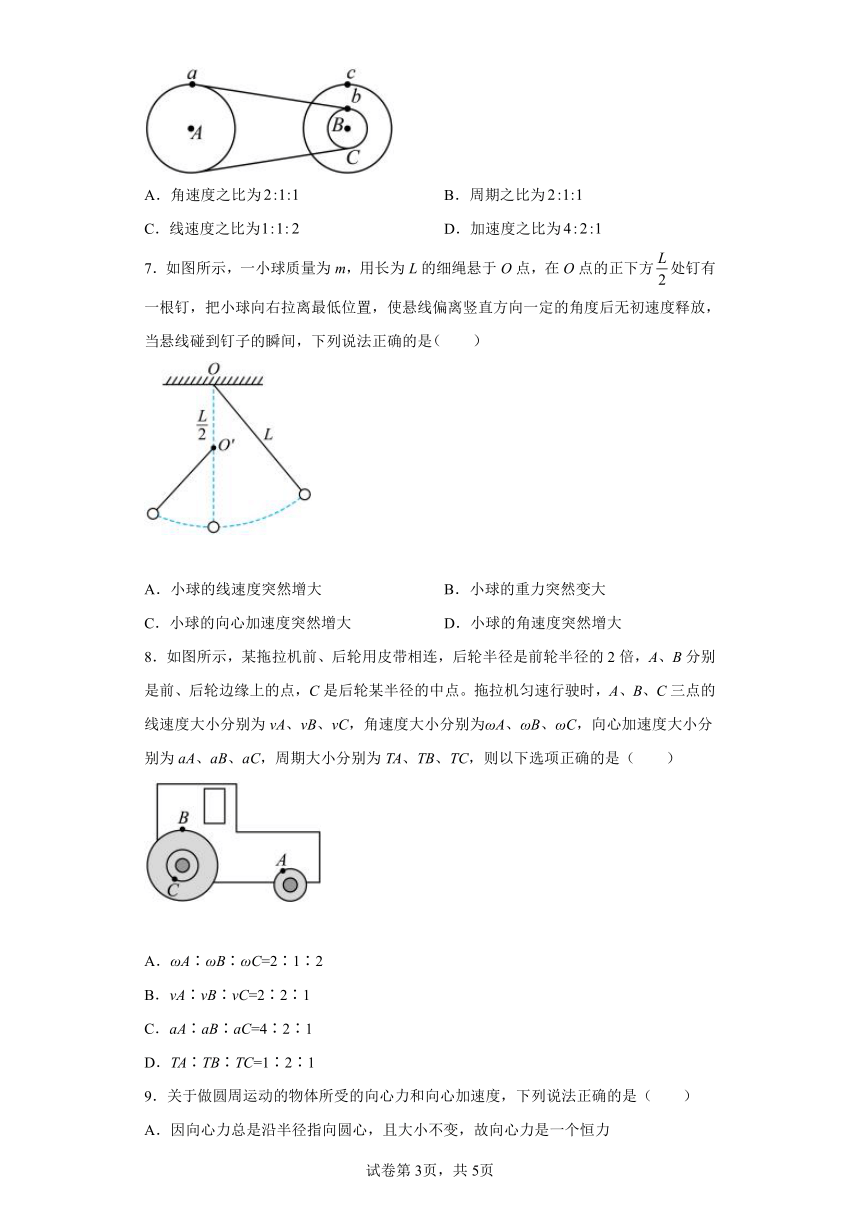
4.如图所示,电动玩具小车在水平桌面上做匀速圆周运动。下列物理量中,可以用来描述小车运动变化快慢的是( )
A.位移 B.路程 C.角速度 D.向心加速度
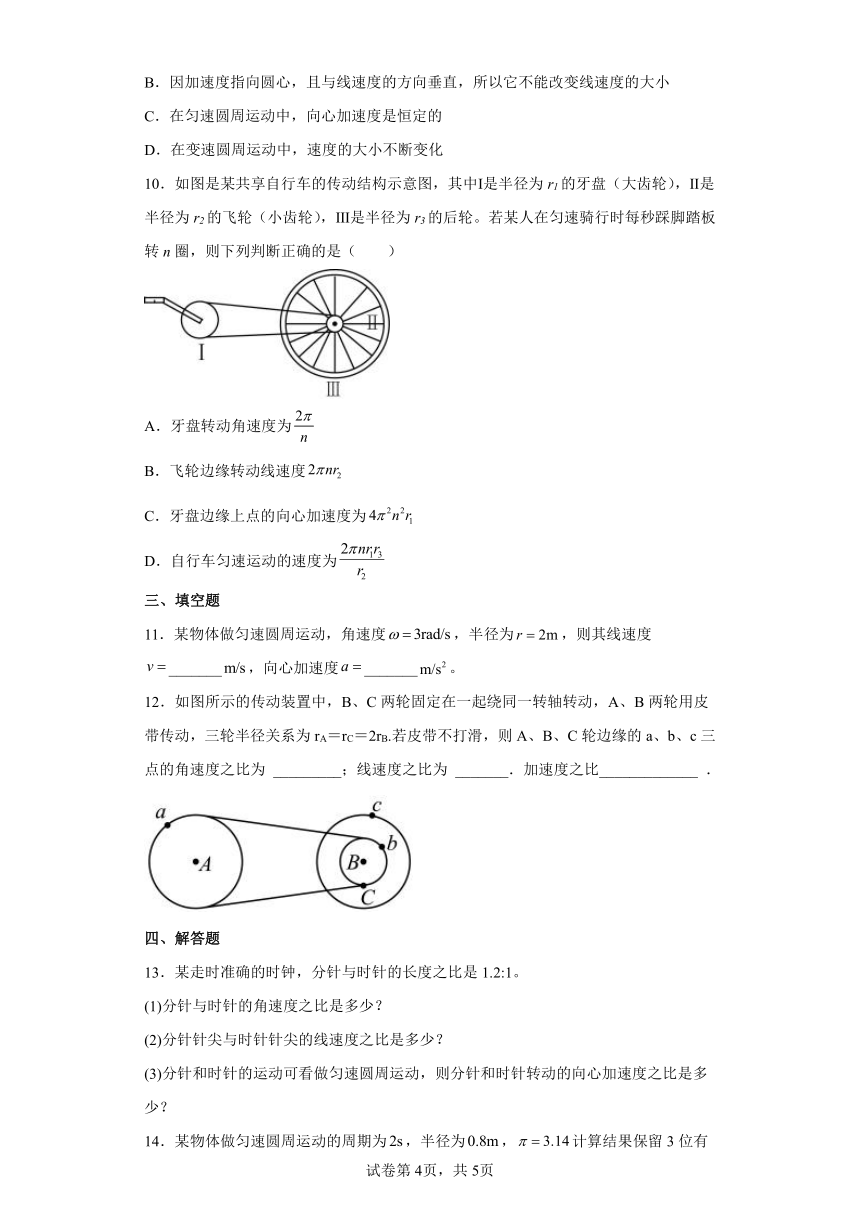
5.自行车的脚踏板、大齿轮、小齿轮、后轮的转动半径不一样.如图所示的四个点甲、乙、丙、丁,则向心加速度与半径成反比的点是( )
A.甲、乙 B.丙、丁
C.甲、丁 D.以上均不对
二、多选题
6.如图所示的传动装置中,、两轮固定在一起绕同一轴转动,A、两轮用皮带传动,三个轮的半径关系是。若皮带不打滑,则A、、三轮边缘上、、三点的( )
A.角速度之比为 B.周期之比为
C.线速度之比为 D.加速度之比为
7.如图所示,一小球质量为m,用长为L的细绳悬于O点,在O点的正下方处钉有一根钉,把小球向右拉离最低位置,使悬线偏离竖直方向一定的角度后无初速度释放,当悬线碰到钉子的瞬间,下列说法正确的是
A.小球的线速度突然增大 B.小球的重力突然变大
C.小球的向心加速度突然增大 D.小球的角速度突然增大
8.如图所示,某拖拉机前、后轮用皮带相连,后轮半径是前轮半径的2倍,A、B分别是前、后轮边缘上的点,C是后轮某半径的中点。拖拉机匀速行驶时,A、B、C三点的线速度大小分别为vA、vB、vC,角速度大小分别为ωA、ωB、ωC,向心加速度大小分别为aA、aB、aC,周期大小分别为TA、TB、TC,则以下选项正确的是( )
A.ωA∶ωB∶ωC=2∶1∶2
B.vA∶vB∶vC=2∶2∶1
C.aA∶aB∶aC=4∶2∶1
D.TA∶TB∶TC=1∶2∶1
9.关于做圆周运动的物体所受的向心力和向心加速度,下列说法正确的是( )
A.因向心力总是沿半径指向圆心,且大小不变,故向心力是一个恒力
B.因加速度指向圆心,且与线速度的方向垂直,所以它不能改变线速度的大小
C.在匀速圆周运动中,向心加速度是恒定的
D.在变速圆周运动中,速度的大小不断变化
10.如图是某共享自行车的传动结构示意图,其中Ⅰ是半径为r1的牙盘(大齿轮),Ⅱ是半径为r2的飞轮(小齿轮),Ⅲ是半径为r3的后轮。若某人在匀速骑行时每秒踩脚踏板转n圈,则下列判断正确的是( )
A.牙盘转动角速度为
B.飞轮边缘转动线速度
C.牙盘边缘上点的向心加速度为
D.自行车匀速运动的速度为
三、填空题
11.某物体做匀速圆周运动,角速度,半径为,则其线速度_______,向心加速度_______。
12.如图所示的传动装置中,B、C两轮固定在一起绕同一转轴转动,A、B两轮用皮带传动,三轮半径关系为rA=rC=2rB.若皮带不打滑,则A、B、C轮边缘的a、b、c三点的角速度之比为 _________;线速度之比为 _______.加速度之比_____________ .
四、解答题
13.某走时准确的时钟,分针与时针的长度之比是1.2:1。
(1)分针与时针的角速度之比是多少?
(2)分针针尖与时针针尖的线速度之比是多少?
(3)分针和时针的运动可看做匀速圆周运动,则分针和时针转动的向心加速度之比是多少?
14.某物体做匀速圆周运动的周期为,半径为,计算结果保留3位有效数字,求:
(1)角速度的大小;
(2)线速度的大小;
(3)向心加速度的大小
15.如图所示,一轿车以30m/s的速率沿半径为60m的圆跑道行驶,当轿车从A运动到B时,轿车和圆心的连线转过的角度为90°,求:
(1)此过程中轿车的位移大小;
(2)此过程中轿车通过的路程;
(3)轿车运动的向心加速度大小.
试卷第1页,共3页
试卷第4页,共5页
参考答案:
1.B
【解析】
【详解】
齿轮A与齿轮B是同缘传动,边缘点线速度相等,根据公式v=ωr可知
而B与C是同轴传动,角速度相等,根据公式v=ωr可知
A.三个点的线速度大小之比为2:2:1,故A错误;
B.三个点的角速度之比为1:4:4,故B正确;
C.根据向心加速度
可知
故三个点的向心加速度之比为1:4:2,故C错误;
D.根据周期可知,三个点的周期之比为
故D错误;
故选B。
2.D
【解析】
【详解】
游客随摩天轮做匀速圆周运动时线速度大小不变,方向沿圆周的切线方向时刻改变,所以的线速度是变化的;而加速度大小
不变,方向指向圆心,也时刻改变;即游客的速度要变化,加速度也要变化。
故选D。
3.D
【解析】
【详解】
A.依题意,两艘快艇的路程之比为,根据线速度的定义式,有
易知,线速度大小之比为4:3。故A错误;
B.依题意,两艘快艇运动方向改变的角度之比是,根据角速度的定义式,有
易知,角速度大小之比为3:2。故B错误;
C.根据角速度与线速度的关系式
易知,圆周运动的半径之比为8:9。故C错误;
D.根据向心加速度的表达式
可得向心加速度大小之比为。故D正确。
故选D。
4.D
【解析】
【详解】
A.位移是描述物体位置的变化,故A不符合题意;
B.路程是运动轨迹的长度,故B不符合题意;
C.角速度是描述小车运动快慢的物理量,故C不符合题意;
D.向心加速度可以用来描述小车运动变化快慢,故D符合题意。
故选D。
5.C
【解析】
【详解】
A.甲、乙两点属于同轴转动,具有相等的角速度,由向心加速度
a=ω2R
可知,甲、乙两点向心加速度与半径成正比,故A错误;
B.丙、丁两点属于同轴转动,具有相等的角速度,由向心加速度
a=ω2R
可知,丙、丁两点向心加速度与半径成正比,故B错误;
CD.甲、丁两点的线速度相等,根据向心加速度的公式
可知,甲、丁两点向心加速度与半径成反比,故C正确,D错误。
故选C。
6.BC
【解析】
【详解】
AC.、两点通过皮带传动,线速度相等,由
可知,角速度1:2,、两点同轴传动,角速度相等,由
可知,线速度1:2,联立可知,、、三点的线速度之比为,角速度之比为,A错误,C正确;
B.由
可得,周期之比为,B正确;
D.由
可得,加速度之比为,D错误。
故选BC。
7.CD
【解析】
【详解】
AB.把小球拉离最低位置后无初速度释放,当悬线碰到钉子的前后瞬间,由于重力与拉力都与速度垂直,所以小球的线速度大小不变,小球的重力也是不变的,AB错误;
C.根据向心加速度公式
可知,线速度大小不变,半径变小,则向心加速度变大,C正确;
D.根据
线速度大小不变,半径变小,则角速度增大,D正确。
故选CD。
8.BC
【解析】
【详解】
选择两轮的中心为参照物,则
B.A、B属于皮带传动,线速度大小相等
B、C属于同轴转动,角速度相同,C是后轮某半径的中点,由
可知
所以
B正确;
A.根据
则
A错误;
C.根据
即
C正确;
D.根据
则
D错误。
故选BC。
9.BD
【解析】
【详解】
A.物体做匀速圆周运动需要向心力,它始终指向圆心,因此方向不断改变,向心力不是恒力,故A错误;
B.由于向心力指向圆心,与线速度方向始终垂直,所以它的效果只是改变线速度方向,不会改变线速度大小。故B正确;
C.在匀速圆周运动中,向心加速度大小不变,方向始终指向圆心即方向时刻变化,则向心加速度是变化的,故C错误;
D.在变速圆周运动中,速度方向沿着切线方向,故在变速圆周运动中,速度的大小和方向都是变化的,故D正确。
故选BD。
10.CD
【解析】
【详解】
A.每秒踩脚踏板转n圈,则大齿轮Ⅰ每一秒转动了n圈,则大齿轮的转动周期
角速度
故A错误;
B.根据题意知:轮I和轮II边缘上的线速度的大小相等,据可知
故B错误;
C.牙盘边缘向心加速度为
故C正确;
D.轮II的角速度
因为轮II和轮III共轴,所以转动的相等,即
自行车匀速运动的速度等于轮III边缘的线速度,根据
可知
故D正确。
故选CD。
11. 6 18
【解析】
【详解】
线速度
向心加速度
12. 1∶2∶2 1∶1∶2 1∶2∶4
【解析】
【详解】
A、B两轮用皮带传动,则;,据得;据得.B、C两轮固定在一起绕同一转轴转动,则;,据得;据得.
综上,,
点睛:同轴传动:被动轮和主动轮的中心在同一根转轴上,主动轮转动使轴转动进而带动从动轮转动,两轮等转速及角速度.皮带传动:两转轮在同一平面上,皮带绷紧与两轮相切,主动轮转动使皮带动进而使从动轮转动,两轮边缘线速度相等.
13.(1)12:1;(2)14.4:1;(3)172.8:1。
【解析】
【详解】
(1)在一个小时的时间内,分针每转过的角度为360度,而时针转过的角度为30度,所以角速度之比为
ω1:ω2=360:30=12:1
(2)由
v=rω
可得,线速度之比为
v1:v2=1.2×12:1×1=14.4:1
(3)根据
a=vω
知,向心加速度之比为
a1:a2=172.8:1
14.(1);(2);(3)
【解析】
【详解】
(1)根据
得
(2)线速度的大小
(3)向心加速度的大小
15.(1) (2) m (3)
【解析】
【详解】
试题分析:(1) 位移是从初位置到末位置的有向线段;
(2) 路程是轨迹的实际长度,等于圆弧长度;
(3) 根据求解向心加速度的大小.
如图所示,v=30m/s,r=60m,θ=90°
(1) 轿车的位移为从初位置A到末位置B的有向线段的长度;
(2) 路程等于弧长 ;
(3) 向心加速度大小
答案第1页,共2页
答案第9页,共1页
一、单选题
1.图为明代出版的《天工开物》中的牛力齿轮,体现我国古代劳动人民的科学智慧。图中A、B、C为该器械的三个齿轮,牛拉动横杆带动齿轮A转动,A与B的轮齿接触良好,B与C通过横轴连接。已知三个齿轮的半径关系为RA=4RB=8RC。当牛做匀速转动时,A、B、C三个齿轮边缘的关系,下列说法正确的是( )
A.线速度之比分别为1:1:2
B.角速度之比分别为1:4:4
C.向心加速度之比4:2:1
D.周期之比1:1:2
2.大型游乐场中有一种叫“摩天轮”的娱乐设施,如图所示,坐在其中的游客随座舱的转动而做匀速圆周运动,以下说法正确的是( )
A.游客的速度不变化,加速度为零
B.游客的速度不变化,加速度也不变化
C.游客的速度要变化,加速度却不变化
D.游客的速度要变化,加速度也要变化
3.A、B两艘快艇在湖面上做匀速圆周运动(如图),在相同的时间内,它们通过的路程之比是,运动方向改变的角度之比是,则它们( )
A.线速度大小之比为 B.角速度大小之比为
C.圆周运动的半径之比为 D.向心加速度大小之比为
4.如图所示,电动玩具小车在水平桌面上做匀速圆周运动。下列物理量中,可以用来描述小车运动变化快慢的是( )
A.位移 B.路程 C.角速度 D.向心加速度
5.自行车的脚踏板、大齿轮、小齿轮、后轮的转动半径不一样.如图所示的四个点甲、乙、丙、丁,则向心加速度与半径成反比的点是( )
A.甲、乙 B.丙、丁
C.甲、丁 D.以上均不对
二、多选题
6.如图所示的传动装置中,、两轮固定在一起绕同一轴转动,A、两轮用皮带传动,三个轮的半径关系是。若皮带不打滑,则A、、三轮边缘上、、三点的( )
A.角速度之比为 B.周期之比为
C.线速度之比为 D.加速度之比为
7.如图所示,一小球质量为m,用长为L的细绳悬于O点,在O点的正下方处钉有一根钉,把小球向右拉离最低位置,使悬线偏离竖直方向一定的角度后无初速度释放,当悬线碰到钉子的瞬间,下列说法正确的是
A.小球的线速度突然增大 B.小球的重力突然变大
C.小球的向心加速度突然增大 D.小球的角速度突然增大
8.如图所示,某拖拉机前、后轮用皮带相连,后轮半径是前轮半径的2倍,A、B分别是前、后轮边缘上的点,C是后轮某半径的中点。拖拉机匀速行驶时,A、B、C三点的线速度大小分别为vA、vB、vC,角速度大小分别为ωA、ωB、ωC,向心加速度大小分别为aA、aB、aC,周期大小分别为TA、TB、TC,则以下选项正确的是( )
A.ωA∶ωB∶ωC=2∶1∶2
B.vA∶vB∶vC=2∶2∶1
C.aA∶aB∶aC=4∶2∶1
D.TA∶TB∶TC=1∶2∶1
9.关于做圆周运动的物体所受的向心力和向心加速度,下列说法正确的是( )
A.因向心力总是沿半径指向圆心,且大小不变,故向心力是一个恒力
B.因加速度指向圆心,且与线速度的方向垂直,所以它不能改变线速度的大小
C.在匀速圆周运动中,向心加速度是恒定的
D.在变速圆周运动中,速度的大小不断变化
10.如图是某共享自行车的传动结构示意图,其中Ⅰ是半径为r1的牙盘(大齿轮),Ⅱ是半径为r2的飞轮(小齿轮),Ⅲ是半径为r3的后轮。若某人在匀速骑行时每秒踩脚踏板转n圈,则下列判断正确的是( )
A.牙盘转动角速度为
B.飞轮边缘转动线速度
C.牙盘边缘上点的向心加速度为
D.自行车匀速运动的速度为
三、填空题
11.某物体做匀速圆周运动,角速度,半径为,则其线速度_______,向心加速度_______。
12.如图所示的传动装置中,B、C两轮固定在一起绕同一转轴转动,A、B两轮用皮带传动,三轮半径关系为rA=rC=2rB.若皮带不打滑,则A、B、C轮边缘的a、b、c三点的角速度之比为 _________;线速度之比为 _______.加速度之比_____________ .
四、解答题
13.某走时准确的时钟,分针与时针的长度之比是1.2:1。
(1)分针与时针的角速度之比是多少?
(2)分针针尖与时针针尖的线速度之比是多少?
(3)分针和时针的运动可看做匀速圆周运动,则分针和时针转动的向心加速度之比是多少?
14.某物体做匀速圆周运动的周期为,半径为,计算结果保留3位有效数字,求:
(1)角速度的大小;
(2)线速度的大小;
(3)向心加速度的大小
15.如图所示,一轿车以30m/s的速率沿半径为60m的圆跑道行驶,当轿车从A运动到B时,轿车和圆心的连线转过的角度为90°,求:
(1)此过程中轿车的位移大小;
(2)此过程中轿车通过的路程;
(3)轿车运动的向心加速度大小.
试卷第1页,共3页
试卷第4页,共5页
参考答案:
1.B
【解析】
【详解】
齿轮A与齿轮B是同缘传动,边缘点线速度相等,根据公式v=ωr可知
而B与C是同轴传动,角速度相等,根据公式v=ωr可知
A.三个点的线速度大小之比为2:2:1,故A错误;
B.三个点的角速度之比为1:4:4,故B正确;
C.根据向心加速度
可知
故三个点的向心加速度之比为1:4:2,故C错误;
D.根据周期可知,三个点的周期之比为
故D错误;
故选B。
2.D
【解析】
【详解】
游客随摩天轮做匀速圆周运动时线速度大小不变,方向沿圆周的切线方向时刻改变,所以的线速度是变化的;而加速度大小
不变,方向指向圆心,也时刻改变;即游客的速度要变化,加速度也要变化。
故选D。
3.D
【解析】
【详解】
A.依题意,两艘快艇的路程之比为,根据线速度的定义式,有
易知,线速度大小之比为4:3。故A错误;
B.依题意,两艘快艇运动方向改变的角度之比是,根据角速度的定义式,有
易知,角速度大小之比为3:2。故B错误;
C.根据角速度与线速度的关系式
易知,圆周运动的半径之比为8:9。故C错误;
D.根据向心加速度的表达式
可得向心加速度大小之比为。故D正确。
故选D。
4.D
【解析】
【详解】
A.位移是描述物体位置的变化,故A不符合题意;
B.路程是运动轨迹的长度,故B不符合题意;
C.角速度是描述小车运动快慢的物理量,故C不符合题意;
D.向心加速度可以用来描述小车运动变化快慢,故D符合题意。
故选D。
5.C
【解析】
【详解】
A.甲、乙两点属于同轴转动,具有相等的角速度,由向心加速度
a=ω2R
可知,甲、乙两点向心加速度与半径成正比,故A错误;
B.丙、丁两点属于同轴转动,具有相等的角速度,由向心加速度
a=ω2R
可知,丙、丁两点向心加速度与半径成正比,故B错误;
CD.甲、丁两点的线速度相等,根据向心加速度的公式
可知,甲、丁两点向心加速度与半径成反比,故C正确,D错误。
故选C。
6.BC
【解析】
【详解】
AC.、两点通过皮带传动,线速度相等,由
可知,角速度1:2,、两点同轴传动,角速度相等,由
可知,线速度1:2,联立可知,、、三点的线速度之比为,角速度之比为,A错误,C正确;
B.由
可得,周期之比为,B正确;
D.由
可得,加速度之比为,D错误。
故选BC。
7.CD
【解析】
【详解】
AB.把小球拉离最低位置后无初速度释放,当悬线碰到钉子的前后瞬间,由于重力与拉力都与速度垂直,所以小球的线速度大小不变,小球的重力也是不变的,AB错误;
C.根据向心加速度公式
可知,线速度大小不变,半径变小,则向心加速度变大,C正确;
D.根据
线速度大小不变,半径变小,则角速度增大,D正确。
故选CD。
8.BC
【解析】
【详解】
选择两轮的中心为参照物,则
B.A、B属于皮带传动,线速度大小相等
B、C属于同轴转动,角速度相同,C是后轮某半径的中点,由
可知
所以
B正确;
A.根据
则
A错误;
C.根据
即
C正确;
D.根据
则
D错误。
故选BC。
9.BD
【解析】
【详解】
A.物体做匀速圆周运动需要向心力,它始终指向圆心,因此方向不断改变,向心力不是恒力,故A错误;
B.由于向心力指向圆心,与线速度方向始终垂直,所以它的效果只是改变线速度方向,不会改变线速度大小。故B正确;
C.在匀速圆周运动中,向心加速度大小不变,方向始终指向圆心即方向时刻变化,则向心加速度是变化的,故C错误;
D.在变速圆周运动中,速度方向沿着切线方向,故在变速圆周运动中,速度的大小和方向都是变化的,故D正确。
故选BD。
10.CD
【解析】
【详解】
A.每秒踩脚踏板转n圈,则大齿轮Ⅰ每一秒转动了n圈,则大齿轮的转动周期
角速度
故A错误;
B.根据题意知:轮I和轮II边缘上的线速度的大小相等,据可知
故B错误;
C.牙盘边缘向心加速度为
故C正确;
D.轮II的角速度
因为轮II和轮III共轴,所以转动的相等,即
自行车匀速运动的速度等于轮III边缘的线速度,根据
可知
故D正确。
故选CD。
11. 6 18
【解析】
【详解】
线速度
向心加速度
12. 1∶2∶2 1∶1∶2 1∶2∶4
【解析】
【详解】
A、B两轮用皮带传动,则;,据得;据得.B、C两轮固定在一起绕同一转轴转动,则;,据得;据得.
综上,,
点睛:同轴传动:被动轮和主动轮的中心在同一根转轴上,主动轮转动使轴转动进而带动从动轮转动,两轮等转速及角速度.皮带传动:两转轮在同一平面上,皮带绷紧与两轮相切,主动轮转动使皮带动进而使从动轮转动,两轮边缘线速度相等.
13.(1)12:1;(2)14.4:1;(3)172.8:1。
【解析】
【详解】
(1)在一个小时的时间内,分针每转过的角度为360度,而时针转过的角度为30度,所以角速度之比为
ω1:ω2=360:30=12:1
(2)由
v=rω
可得,线速度之比为
v1:v2=1.2×12:1×1=14.4:1
(3)根据
a=vω
知,向心加速度之比为
a1:a2=172.8:1
14.(1);(2);(3)
【解析】
【详解】
(1)根据
得
(2)线速度的大小
(3)向心加速度的大小
15.(1) (2) m (3)
【解析】
【详解】
试题分析:(1) 位移是从初位置到末位置的有向线段;
(2) 路程是轨迹的实际长度,等于圆弧长度;
(3) 根据求解向心加速度的大小.
如图所示,v=30m/s,r=60m,θ=90°
(1) 轿车的位移为从初位置A到末位置B的有向线段的长度;
(2) 路程等于弧长 ;
(3) 向心加速度大小
答案第1页,共2页
答案第9页,共1页
